MinHash-LSH：如何解决医学大模型的大规模数据去重？

MinHash-LSH 最小哈希 + 局部敏感哈希：如何解决医学大模型的大规模数据去重？

大模型的数据问题
MinHash-LSH 最小哈希 + 局部敏感哈希：大规模数据集去重优化
Jaccard相似度：用于比较样本集之间的相似性
降维技术 Minhash
LSH – 局部敏感哈希

MinHash-LSH 多个开源数据集去重

大模型的数据问题

问题：训练医学大模型的数据规模真的很大，其中会夹杂很多重复数据。

临床数据：

20 亿条文本数据

教材数据：

1000+ 本指南
7万+ 药品说明书
N 个科室疾病培训数据
N 本古籍、教材
…

开源数据：

中文医学命名实体识别CMedEE
中文医学文本实体关系抽取CMedIE
临床术语标准化任务CHIP-CDN
临床试验筛选标准短文本分类CHIP-CTC
平安医疗科技疾病问答迁移学习CHIP-STS
医疗搜索检索词意图分类KUAKE-QIC
医疗搜索查询词—页面标题相关性KUAKE-QTR
医疗搜索查询词—查询词相关性KUAKE-QQR
中文医学命名实体识别CMedEE
中文医学文本实体关系抽取CMedIE
临床术语标准化任务CHIP-CDN
临床试验筛选标准短文本分类CHIP-CTC
平安医疗科技疾病问答迁移学习CHIP-STS
医疗搜索检索词—意图分类KUAKE-QIC
医疗搜索查询词—页面标题相关性KUAKE-QTR
医疗搜索查询词—查询词相关性KUAKE-QQR
医疗搜索查询词—相关性检索KUAKE-IR
阴阳性实体判别CHIP-MDCFNPC
对话实体抽取IMCS-V2-NER
意图标签分类IMCS-V2-DAC
智能诊疗对话症状识别IMCS-V2-SR
诊疗报告生成IMCS-V2-MRG
医疗对话生成MedDG
MedDialog-CN https://github.com/UCSD-AI4H/Medical-Dialogue-System
IMCS-V2 https://github.com/lemuria-wchen/imcs21
CHIP-MDCFNPC https://tianchi.aliyun.com/dataset/95414
MedDG https://tianchi.aliyun.com/dataset/95414
cMedQA2 https://github.com/zhangsheng93/cMedQA2
Toyhom https://github.com/Toyhom/Chinese-medical-dialogue-data
michaelwzhu/ChatMed-Consult michaelwzhu/ChatMed-Consult · Hugging Face
Huatuo-26M https://github.com/FreedomIntelligence/Huatuo-26M
Medical https://huggingface.co/datasets/shibing624/medical
复旦DISC-MedLLM https://github.com/FudanDISC/DISC-MedLLM
DoctorGLM https://zhuanlan.zhihu.com/p/657058443
MedicalGPT https://zhuanlan.zhihu.com/p/657058443
ChatMed：https://zhuanlan.zhihu.com/p/657058443
MedQA-ChatGLM：https://zhuanlan.zhihu.com/p/657058443
神农中医药大模型：https://zhuanlan.zhihu.com/p/657058443
70B医学大模型：https://huggingface.co/datasets/epfl-llm/guidelines
澳门理工caregpt：https://github.com/WangRongsheng/CareGPT

MinHash-LSH 最小哈希 + 局部敏感哈希：大规模数据集去重优化

怎么去重呢？

要用到一个炒鸡牛逼的算法：MinHash-LSH。

谷歌、亚马逊等公司的许多核心功能都是 MinHash-LSH 实现的。

解法：MinHash-LSH
问题特征：能在大数据中，寻找特征向量相似又不完全相同的情况下，找出尽可能近的样本。
应用场景：亚马逊根据相似度最高的买家的购买历史找到新的商品推荐、谷歌搜索字词与 Google 的索引互联网之间执行相似性搜索、Spotify根据用户音乐风格，寻找匹配的相似度

当有 30 亿级别的集合需要比较时，使用传统的全对全比较方法（即比较任意两个集合是否相似）将变得非常耗时，这种方法的时间复杂度是 O(n^2)，随着集合数量的增加，所需的计算时间呈平方级增长。

在很多实际情况下，绝大多数的集合对之间都不相似，这意味着全对全比较中的大部分计算实际上是无用功。

如果能有一种方法能够快速地将可能相似的集合对筛选出来，只对这些潜在相似的集合对进行详细的相似度计算，那么就可以大幅度降低计算成本。

MinHash 和局部敏感哈希（LSH）就是这样一种解决方案：

MinHash 是一种哈希技术，可以用来有效地估计集合之间的Jaccard相似度
LSH 是用来将那些相似度高的集合哈希到相同的桶中的技术。

只有被哈希到同一个桶中的集合对才需要进行相似度比较，大大减少了比较的数量，从而降低了算法的整体时间复杂度。

时间复杂度从平方量级降低到接近线性复杂度。

MinHash-LSH 的设计逻辑：

一般的hash，原内容发生微小变化后，hash值的变化是无法预估的。
字符串改一个字母后，整个字符串md5变得完全不一样，图片改一个像素后hash值也变得完全不一样。
局部敏感hash的改进在于，原内容发生微小变化后，其hash值也只发生微小变化。
从而满足原内容相近hash值也相近的良好性质。
这种性质的好处在于，可以在hash空间进行近邻检索。

怎么实现这种逻辑呢？

从对内容敏感的信息，变成，对位置敏感的哈希
这种哈希算法，得到的哈希值（或者说指纹），在向量空间中的位置是“敏感”的
两个指纹在向量空间中的相对位置是有意义的，近就是真的近，远就是真的远
而不是如md5一样，在向量空间中的远近和实际含义的远近无关系

Jaccard相似度：用于比较样本集之间的相似性

Jaccard相似度的定义是两个集合交集大小与并集大小之比。

具体来说，如果有两个集合A和B，那么ta们之间的 Jaccard 相似度：

$\frac{|A \cap B|}{|A \cup B|} ]$

$∣ A \cap B ∣$ 表示集合A和集合B的交集中元素的数量。

$∣ A \cup B ∣$ 表示集合A和集合B的并集中元素的数量。

举个列子，集合X = {a,b,c}，Y = {q,a,b}。

那 Jac(X,Y) = 2 / 3 = 0.67。

X 和 Y 有 67% 的元素相同。

Jaccard相似度的值范围在0到1之间：

0 表示没有共同元素，即两个集合完全不相似
1 表示两个集合完全相同
在0到1之间的值表示集合之间的部分相似性

Jaccard相似度越高，表示两个集合的相似度越大。

在数据处理中，我们可以使用 jieba 分词库，把一句话分词成各个元素后，计算相似度。

query1 = ["ta喜欢的水果有？"]                          # 分词前
query1 = ['ta', '喜欢', '的', '水果', '有', '？']      # 分词后

query2 = ["ta喜欢的坚果有？"]                          # 分词前
query2 = ['ta', '喜欢', '的', '坚果', '有', '？']      # 分词后

降维技术 Minhash

直接计算数据之间的相似度（Jaccard相似度）会非常耗时，每个集合里面的元素，俩俩比较。

如果大部分集合对之间的相似度都很低，进行俩俩比较会做很多无用功。

传统的方法需要对两个集合的每个元素进行一对一的比较，以确定ta们的相似性。

MinHash 算法通过为每个集合生成一个固定长度的标签（哈希函数产生签名），来代表集合的特征。

原本复杂的集合相似性比较，简化为标签（MinHash值）的比较
比较签名的成本，远低于比较完整的集合

这些签名保留了集合间相似度的信息，还能保持原始数据的相似性。

如果两个集合很相似，Minhash 值也会很相似

但单个 MinHash 值可能无法准确地反映两个集合的相似性，可能是一个偶然的匹配。

在实际应用中，我们会使用数百或数千个哈希函数来增加估计的准确性。

如果大多数哈希函数产生的MinHash值都相同，我们可以有更高的信心认为两个集合是相似的。

解法：MinHash
问题特征：在高维空间中估计稀疏数据集合的相似性，特别是当直接计算成对相似度不可行时。如需要快速而精确地估计大型数据集中集合之间的Jaccard相似度。
应用场景：文本处理中比较文档相似性，如新闻聚类、查重系统；生物信息学中比较基因组序列；推荐系统中评估用户间或物品间的相似性。

这里是为了应用，具体数学公式、概率证明，请猛击《原始论文》。

LSH – 局部敏感哈希

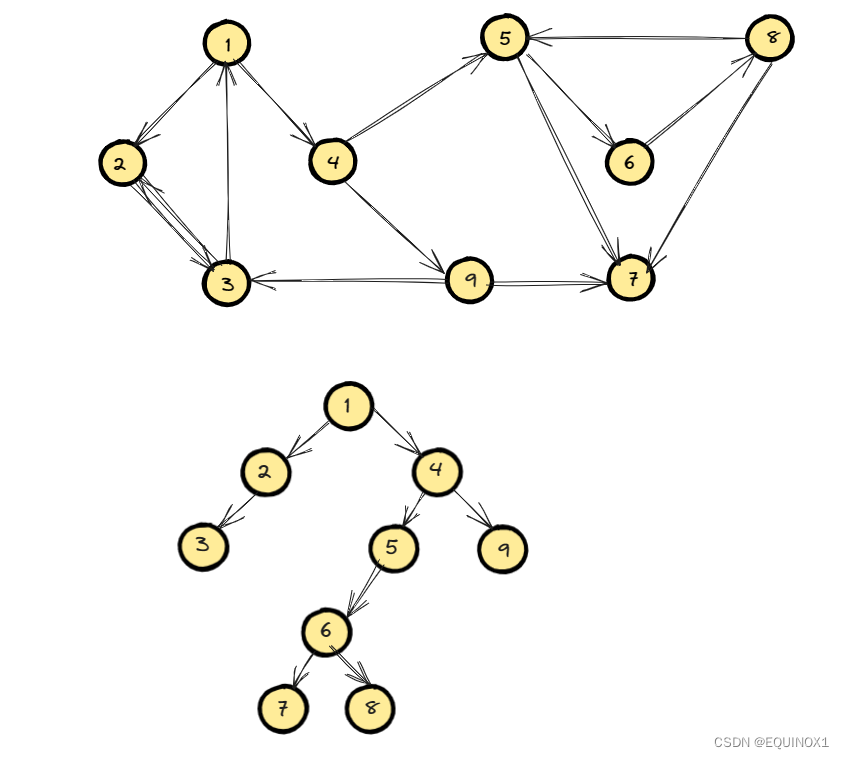
LSH 函数旨在将相似的值放入相同的存储桶中。

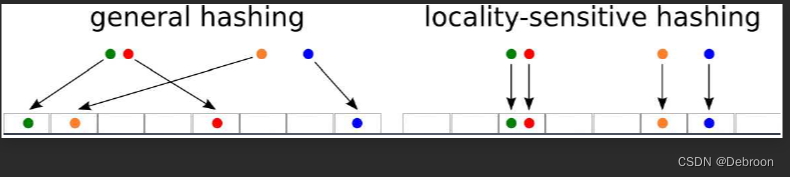
LSH 的核心思想是将相似的数据点映射到相同的“桶”（buckets）中，而不相似的点映射到不同的桶中。

这样，当需要找到一个数据点的最近邻时，可以仅在相同桶中的点之间进行搜索，而不是在整个数据集中搜索，大大降低了计算量。

LSH 是基于哈希的技术，其特点是保持局部相似性：相似的输入在哈希后应该产生相似或相同的哈希值。

与传统哈希函数不同，LSH 的目的不是为了避免冲突，而是为了让冲突更可能发生在相似的项之间。

LSH 的具体实现方式有很多，最常见的包括：

MinHash LSH：适用于度量集合相似性（如Jaccard相似性）的LSH。MinHash 将每个集合转换成一个固定长度的签名，该签名是由多个最小哈希值组成的向量，这些最小哈希值由集合中的元素通过多个哈希函数计算得到。
SimHash LSH：用于处理高维特征向量的文本或其他数据的相似性。SimHash 通过哈希函数将特征向量转换为一个固定长度的位串，这样，相似的数据点会产生相似的位串。
Euclidean LSH：适用于欧几里得空间中的数据点。它使用超平面将空间划分成不同的区域，并将落在同一区域内的点映射到同一个桶中。

LSH 算法的详细步骤如下：

选择适合的 LSH 家族：根据数据的性质和相似性度量选择合适的 LSH 函数。
定义哈希表和哈希函数：创建多个哈希表，并为每个哈希表定义一个或多个 LSH 函数。
哈希和存储数据点：使用定义的哈希函数将数据点映射到各自的桶中。
查询过程：在查询最近邻时，首先计算查询点的哈希值，然后只在对应桶中的点集合中进行搜索，这样可以快速缩小搜寻范围。

LSH 的效率和精度受到哈希函数个数、哈希表数量和桶的大小等参数的影响。

在应用中，这些参数需要根据具体应用进行调整以达到最佳效果。

由于 LSH 是一种概率算法，允许少量的误报（false positives）和漏报（false negatives），但在实际应用中，这通常是可接受的，特别是在处理大规模数据集时，ta提供了显著的速度优势。

解法：LSH（局部敏感哈希）
问题特征：当数据量很大，使得对所有可能的数据对进行比较变得不可行时，需要一种方法能够高效地查找和查询近似最近邻
应用场景：大规模图像或视频检索系统，寻找视觉上相似的内容；文本或文章数据库中寻找相似文档；音频或声音样本匹配；大型数据库中的快速相似项查找

MinHash-LSH 多个开源数据集去重

配置环境包：

pip install jieba datasketch

MinHash-LSH 代码：

import jieba
import re  # 假设这里应该导入 re 而不是 ro
from datasketch import MinHash, MinHashLSH

query = "想人想得厉害的时候，也是淡淡的。像饿了很多日的旅人闻到炊烟，但知道不是自家的。"

sentences = ["想人想得厉害的时候，也是轻轻的。像漂泊很多日的旅人闻到炊烟，但知道不是返乡的。",
             "梦中梦见心上人,也是轻轻的。像漂泊良久的游子见到归帆，却明白并非返乡的。"]

regex = re.compile("，|。")

def split_word(sentence):
    global regex
    return [word for word in jieba.lcut(re.sub(regex, '', sentence)) if word.strip()]

query_lcut = split_word(query)
sentences_lcut = [split_word(sentence) for sentence in sentences]
print(query_lcut)
print(sentences_lcut)

'''
print(query_lcut)：
['想人', '想', '得', '厉害', '的', '时候', '也', '是', '淡淡的', '像', '饿', '了', '很多', '日', '的', '旅人', '闻到', '炊烟', '但', '知道', '不是', '自家', '的']
[]

print(sentences_lcut)：[
['想人', '想', '得', '厉害', '的', '时候', '也', '是', '轻轻', '的', '像', '漂泊', '很多', '日', '的', '旅人', '闻到', '炊烟', '但', '知道', '不是', '返乡', '的']
['梦中', '梦见', '心上人', ',', '也', '是', '轻轻', '的', '像', '漂泊', '良久', '的', '游子', '见到', '归帆', '却', '明白', '并非', '返乡', '的']
'''

threshold = 0.5   # 相似度 > 0.5
num_perm = 128
lsh = MinHashLSH(threshold=threshold, num_perm=num_perm)
for idx, sentence_lcut in enumerate(sentences_lcut):
    minhash = MinHash(num_perm=num_perm)
    minhash.update_batch([word.encode('utf-8') for word in sentence_lcut])
    lsh.insert("minhash_sentence_{}".format(idx+1), minhash)

print(list(lsh.keys))
# 输出：['minhash_sentence_1', 'minhash_sentence_2']

minhash_query = MinHash(num_perm=num_perm)
minhash_query.update_batch([word.encode('utf-8') for word in query_lcut])
simi_result = lsh.query(minhash_query)
print("Jaccard相似度 > {} 的句子有：{}".format(threshold, simi_result))
# 输出：Jaccard相似度 > 0.5 的句子有：['minhash_sentence_1']  
 
 
# 删除 minhash_sentence_1，从 LSH 中移除查询到的结果，需要对 simi_result 进行遍历
for key in simi_result:
    lsh.remove(key)

print(list(lsh.keys))
# 输出：['minhash_sentence_2']

去重多个开源文件所有数据：

import jieba
import re
from datasketch import MinHash, MinHashLSH

# 此函数用于分词
def split_word(sentence):
    regex = re.compile("，|。|？|！")
    return [word for word in jieba.lcut(re.sub(regex, '', sentence)) if word.strip()]

# 配置参数
threshold = 0.5   # 相似度阈值
num_perm = 128    # MinHash的排列次数

# 初始化LSH对象
lsh = MinHashLSH(threshold=threshold, num_perm=num_perm)

# 假设你有一个函数来获取多个开源文件下所有问答对
# def get_qa_pairs():
#     # 这里应该包含读取文件并返回所有问答回答的代码
#     return qa_pairs

# 读取所有问答回答对
qa_pairs = get_qa_pairs()

# 为每个问答回答创建MinHash并加入LSH
for idx, qa_pair in enumerate(qa_pairs):
    q, a = qa_pair                                   # 假设qa_pair是一个包含问题和答案的元组
    combined_text = q + " " + a                      # 可以根据需要将问题和答案合并或分别处理
    words = split_word(combined_text)
    minhash = MinHash(num_perm=num_perm)
    for word in words:
        minhash.update(word.encode('utf-8'))
    lsh.insert("qa_pair_{}".format(idx), minhash)

# 查询并去重
unique_qa_pairs = []
for idx, qa_pair in enumerate(qa_pairs):
    q, a = qa_pair
    combined_text = q + " " + a
    words = split_word(combined_text)
    minhash = MinHash(num_perm=num_perm)
    for word in words:
        minhash.update(word.encode('utf-8'))
    # 查询相似问答回答
    result = lsh.query(minhash)
    # 如果只有自己或没有其他相似项，则视为唯一
    if len(result) <= 1 or (len(result) == 2 and "qa_pair_{}".format(idx) in result):
        unique_qa_pairs.append(qa_pair)
        # 将此问答回答标记为唯一，可选步骤
        lsh.remove("qa_pair_{}".format(idx))

# 输出去重后的问答对
print(unique_qa_pairs)