会旋转的树,你见过吗?

news2024/10/7 20:29:24

🎈个人主页:🎈 :✨✨✨初阶牛✨✨✨
🐻强烈推荐优质专栏: 🍔🍟🌯C++的世界(持续更新中)
🐻推荐专栏1: 🍔🍟🌯C语言初阶
🐻推荐专栏2: 🍔🍟🌯C语言进阶
🔑个人信条: 🌵知行合一
🍉本篇简介:>:AVL树的实现，旋转的详细分析，抽象图，具体图分步骤讲解，保姆级教学。
金句分享:
✨人生若只如初见，✨
✨何事秋风悲画扇。✨

前言

前面我们学习了二叉搜索树,二叉搜索树如果左右子树高度相差不大,那么效率还是可观的,比如:满二叉搜索树的查询效率为 O(logn).
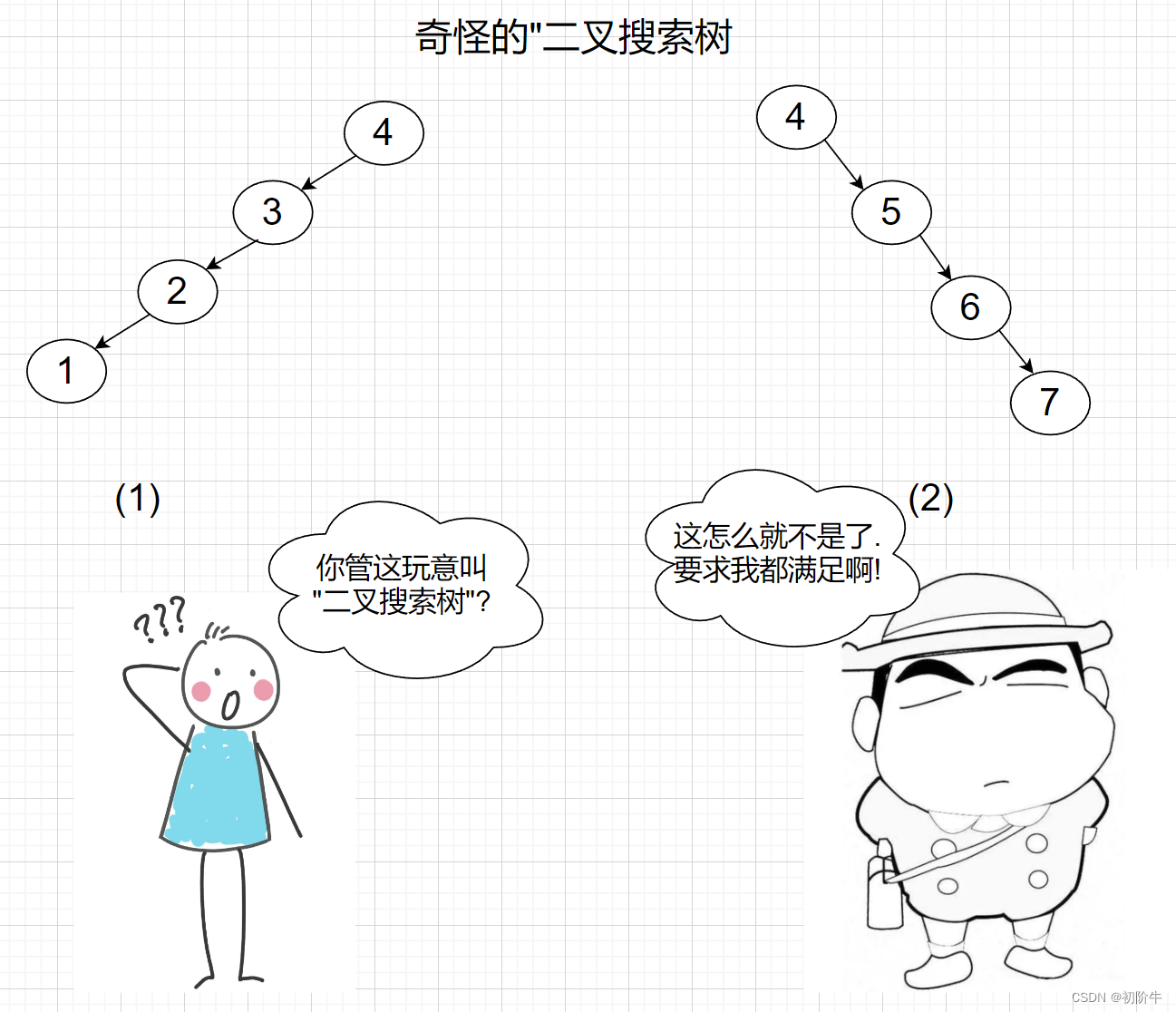
但是,如果插入的数据是有序的,或者大部分有序,则会导致 “二叉搜索树” 退化为类似于链表的结构.
那链表查询数据的时间复杂度牛牛就不用多说了吧.答案: O(n)

示例:
在这里插入图片描述

目录

  • 前言
  • 一、AVL树的介绍
  • 二、AVL树的模拟实现
    • 🍭结点类
    • 🍔AVL树的框架:
    • 2.1 "插入"操作(重点)
      • ①:右旋
        • (1) 右旋具体图:
        • (2)右旋抽象图:
      • ②左旋:
        • (1)左旋具体图:
        • (2)左旋抽象图
      • ③右左双旋
        • （1）右左双旋具体图
        • （2）右左双旋抽象图
      • ④左右双旋
        • （1）左右双旋具体图
        • （2）左右双旋抽象图
      • "插入"操作的代码实现:
    • 2.2 中序遍历:
    • 2.3 AVL树的"高度"
    • 2.4 验证AVL树
  • 结语

一、AVL树的介绍

AVL树是一种自"平衡二叉搜索树"，它的每个节点存储一个关键字，具有以下特点：

  1. 每个节点的左右子树高度差至多为1，也就是说，AVL树的任何一个节点的左右子树高度差不超过1。

  2. 对于任意一个节点，其左子树和右子树都是一个AVL树。

  3. AVL树中的每个节点都能保证左子树中的所有节点小于当前节点的关键字，右子树中的所有节点大于当前节点的关键字。(也就是满足二叉搜索树的性质)

如果我们定义 平衡因子=右子树的高度-左子树的高度
则树中每个结点的平衡因子的绝对值 不超过1 即可以为( 1 0 -1三种)
1:表示右子树比左子树高.
0:表示左子树和右子树一样高.
-1:表示左子树比右子树高.

每当向AVL树中插入、删除节点时，AVL树会自动地进行旋转操作将树变为平衡状态，从而保证了AVL树的平衡性。

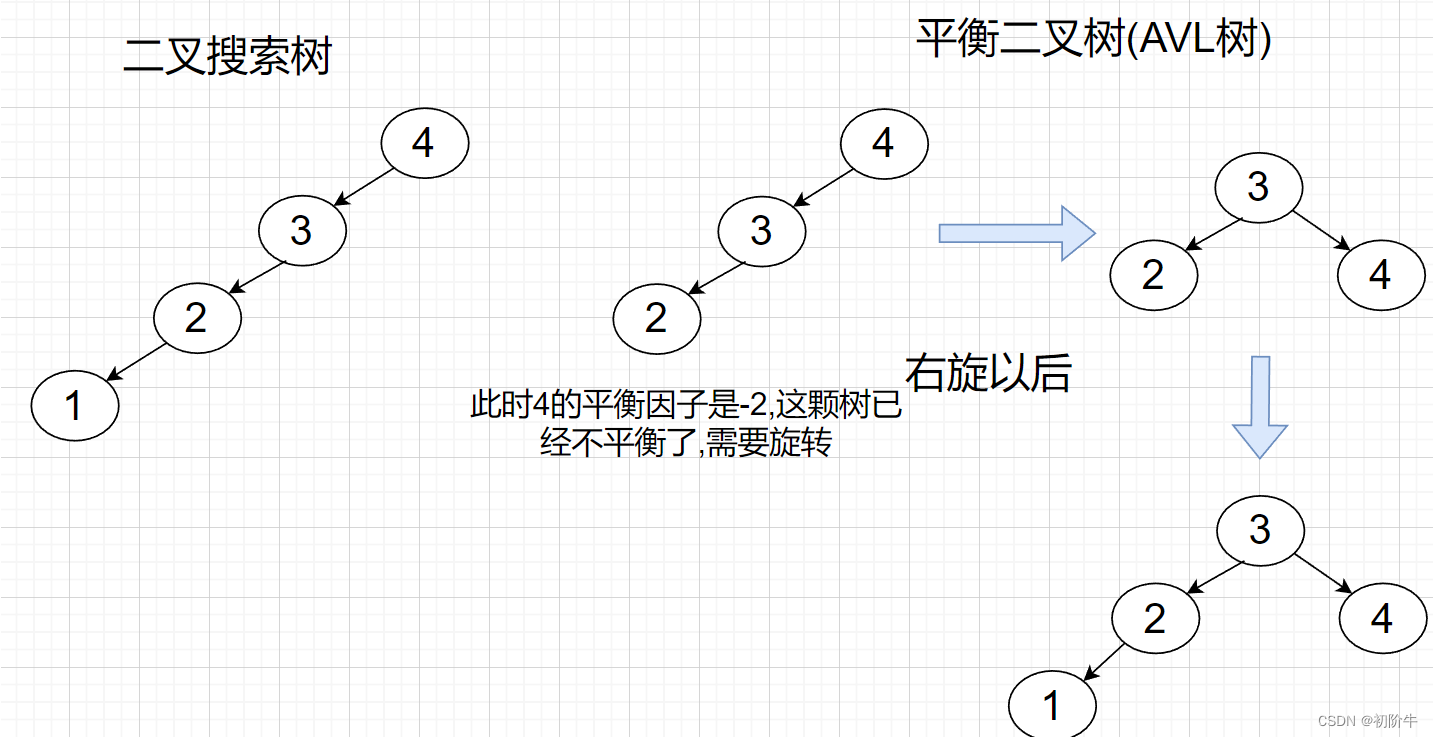
在这里插入图片描述
会旋转的树才够强,AVL树的查询数据的时间复杂度总是控制在 O(logn)量级.

二、AVL树的模拟实现

补充知识点:
在c++中 pair类是一个模板类,用于将两个值组成一个单元,也就是我们称为的键值对.

template<class T1, class T2>
struct pair {
    typedef T1 first_type;
    typedef T2 second_type;

    T1 first;  // 第一个元素
    T2 second; // 第二个元素

    // 默认构造函数
    pair() : first(T1()), second(T2()) {}
    // 初始化构造函数
    pair(const T1& x, const T2& y) : first(x), second(y) {}
};

🍭结点类

没错,AVL树是三叉树,为了方便旋转,我们需要多存储一个指针域(_parent) ,指向父节点.

template<class K, class V>
struct AVLTreeNode
{
	pair<K, V> _kv;							//键值对
	AVLTreeNode<K, V>* _left;				//左子树
	AVLTreeNode<K, V>* _right;				//右子树
	AVLTreeNode<K, V>* _parent;				//父节点
	int _bf;								// balance factor平衡因子

	//构造
	AVLTreeNode(const pair<K, V>& kv)
		:_kv(kv)
		, _left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _bf(0)
	{}
};

🍔AVL树的框架:

// AVL树的结构
template<class K,class V>
class AVLTree
{
	typedef AVLTreeNode<K,V> Node;		
public:
	AVLTree()
		: _root(nullptr)
	{}

	// 在AVL树中插入值为data的节点
	bool Insert(const pair<K, V>& kv);
	void  InOrder();

	// AVL树的验证
	bool IsAVLTree(){
		return _IsAVLTree(_root);
	}

private:
	// 根据AVL树的概念验证proot是否为有效的AVL树
	bool _IsAVLTree(Node* root);
	size_t _Height(Node* root);
	void  _InOrder(Node* root);
	
	// 右单旋
	void RotateR(Node* parent);
	// 左单旋
	void RotateL(Node* parent);
	// 右左双旋
	void RotateRL(Node* parent);
	// 左右双旋
	void RotateLR(Node* parent);

private:
	Node* _root;
};

2.1 "插入"操作(重点)

注意: 本篇实现的AVL树,平衡因子是右子树高度—左子树高度.

故:
当新增结点在父亲结点的左边时,左子树的高度+1,则平衡因子-1.
当新增结点在父亲结点的右边时,右子树的高度+1,则平衡因子+1.
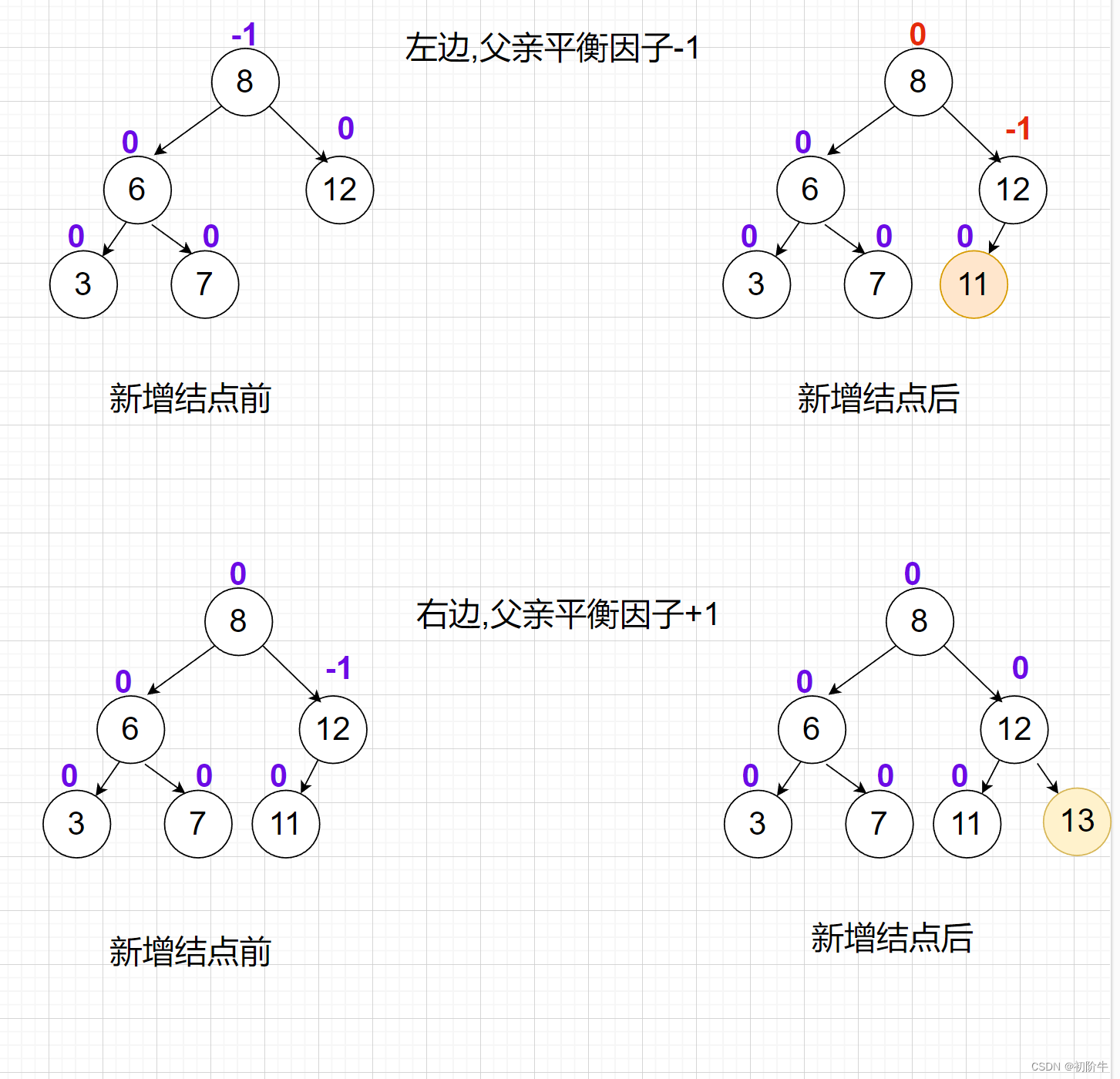
在这里插入图片描述
子树的平衡因子变化,可能会影响祖先路径上的结点,需要继续向上更新.

(1) 当新增结点后,父节点的平衡因子变成0,则插入结束.
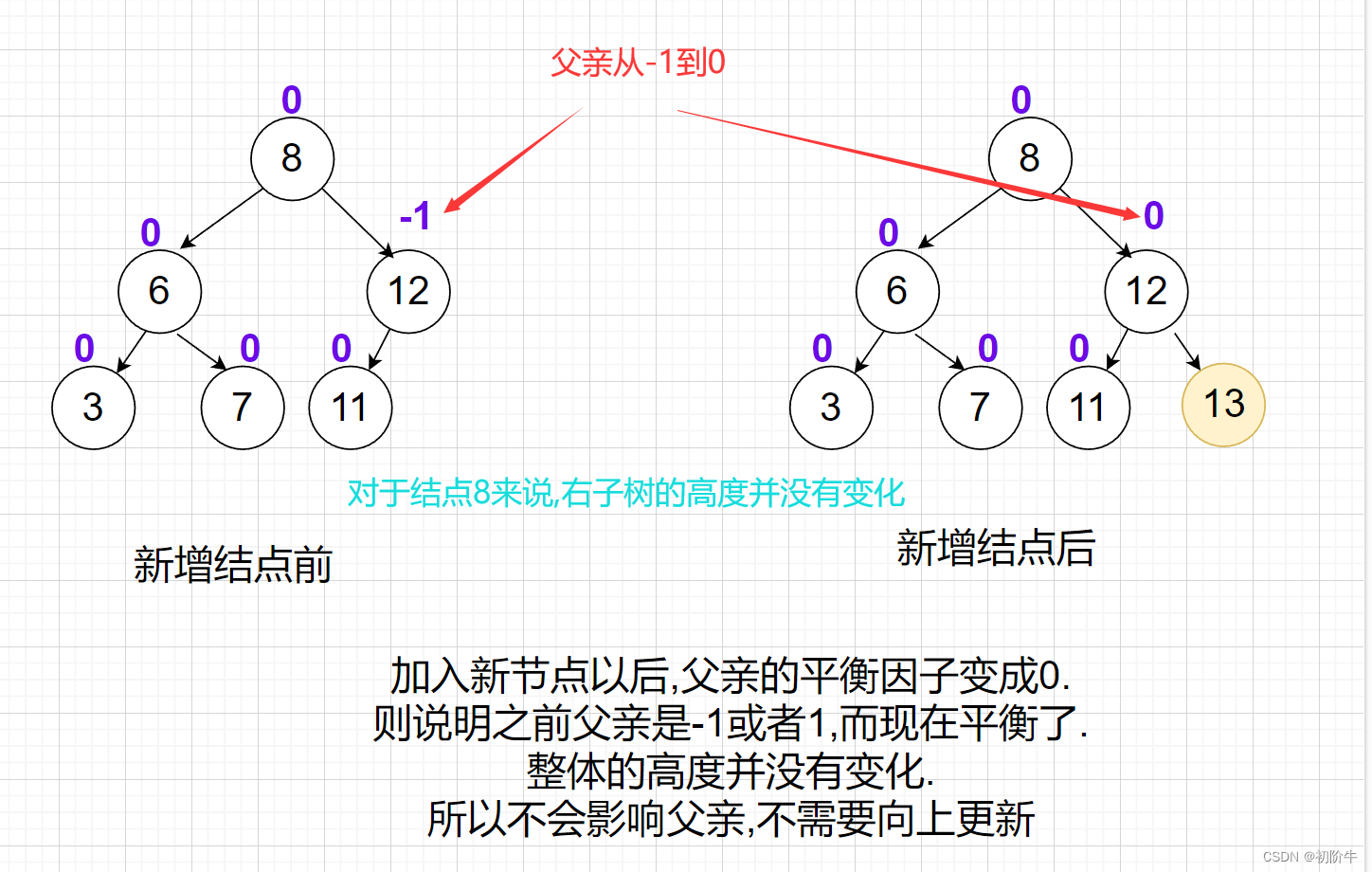
在这里插入图片描述
(2) 当新增结点后,父节点的平衡因子变成1或者-1,则需要向上更新.

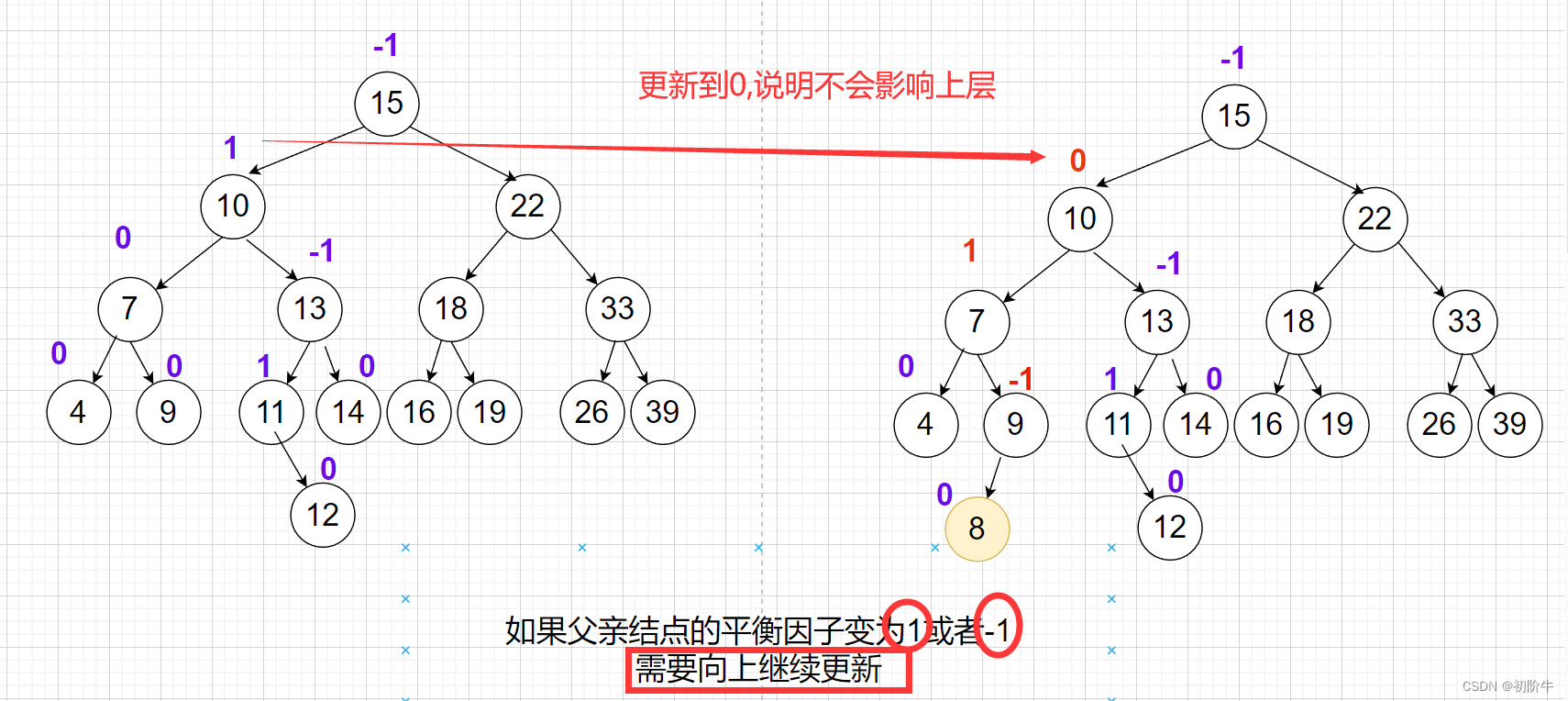
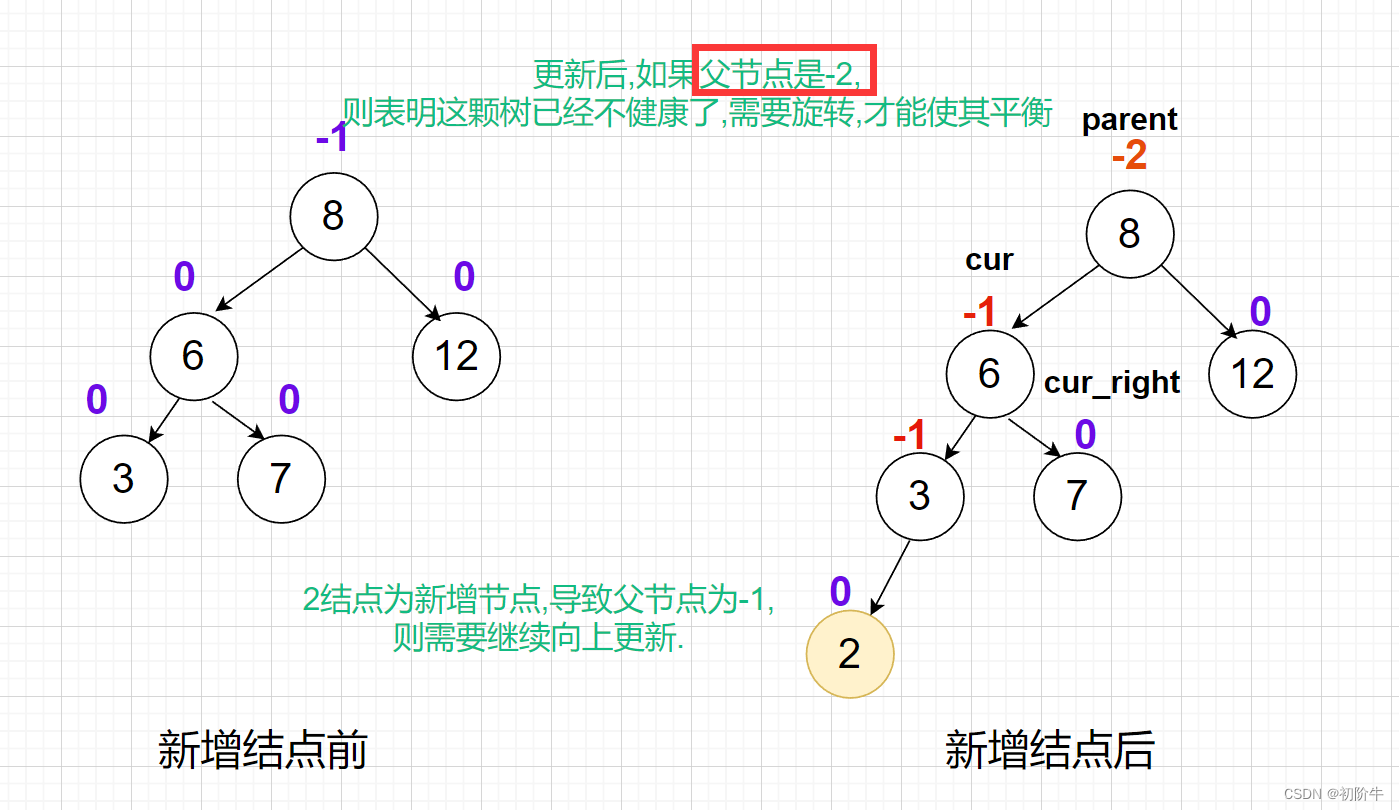
在这里插入图片描述
(3)当新增结点后,父节点的平衡因子变成2或者-2需要旋转.

①:右旋

当继续向上更新到父节点是平衡因子-2时,则需要右旋.
因为左边比右边高,需要旋转到右边.使其平衡.

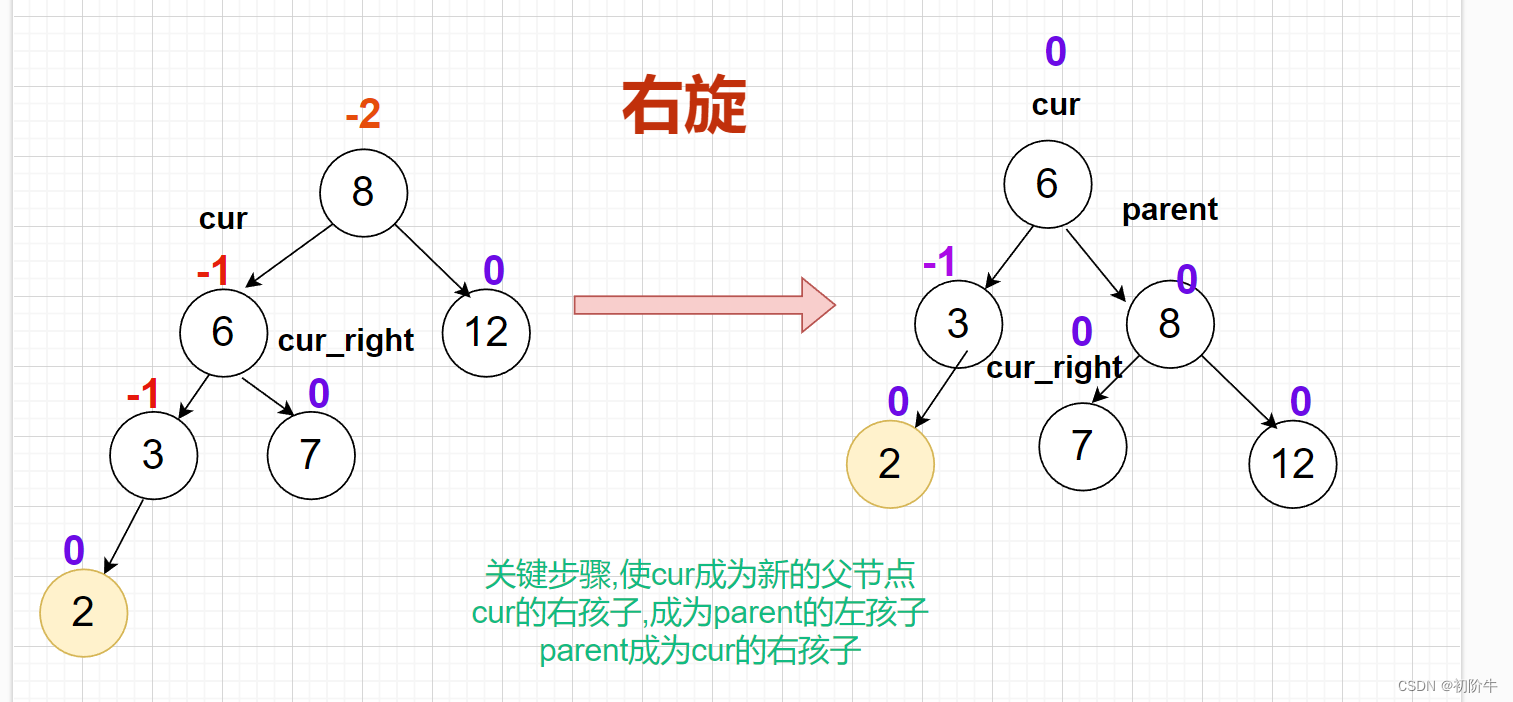
(1) 右旋具体图:

在这里插入图片描述

关键步骤:

使cur成为新的父节点
cur的右孩子,成为parent的左孩子
parent成为cur的右孩子
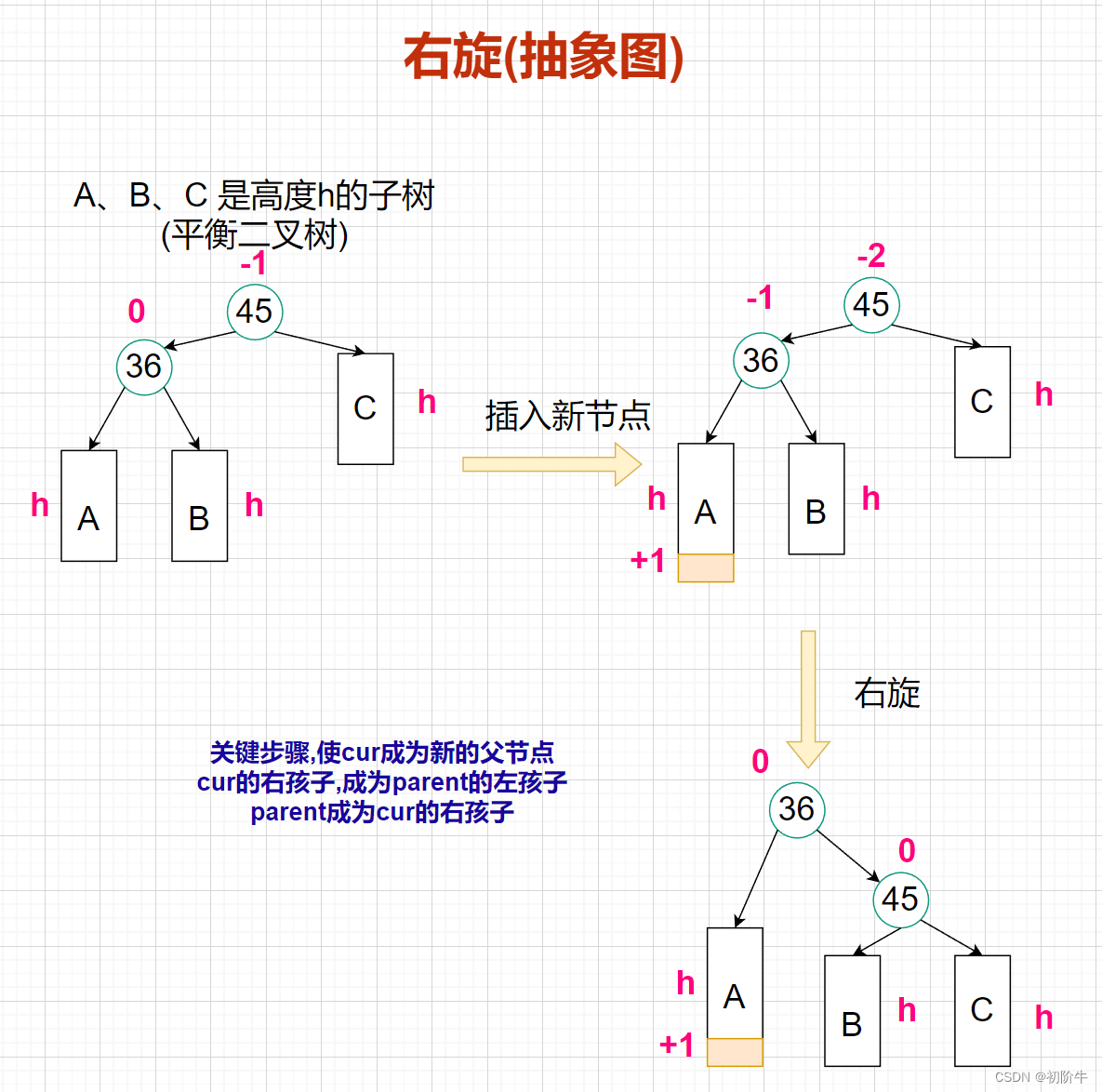
在这里插入图片描述

(2)右旋抽象图:

在这里插入图片描述

更新平衡因子:
从抽象图可以看出,右旋旋转后,平衡因子cur parent都可以无脑设置为0.

代码实现:

//右旋
template<class K,class V>
void AVLTree<K,V>::RotateR(Node* parent)
{
	Node* ppnode = parent->_parent;
	Node* cur = parent->_left;
	Node* cur_right = cur->_right;

	//cur的右子树变成parent的左子树
	if (cur_right) {					//cur_right  可能不存在
		parent->_left = cur_right;
		cur_right->_parent = parent;//保持三叉连
	}
	else {
		parent->_left = nullptr;
	}
	//parent变成cur的右子树
	cur->_right = parent;		
	parent->_parent = cur;//保持三叉连


	if (ppnode) {		
		cur->_parent = ppnode;

		if (ppnode->_left == parent) {		//如果是上面的左子树
			ppnode->_left = cur;
		}
		else {
			ppnode->_right = cur;			//如果是上面的右子树
		}
	}
	else {									//如果ppnode是nullptr,则代表parent为root
		_root = cur;
		cur->_parent = nullptr;
	}
	
	parent->_bf = 0;
	cur->_bf = 0;
}

②左旋:

当继续向上更新到父节点平衡因子是2时,则需要左旋.
因为右边比左边高,需要旋转到左边,使其平衡.

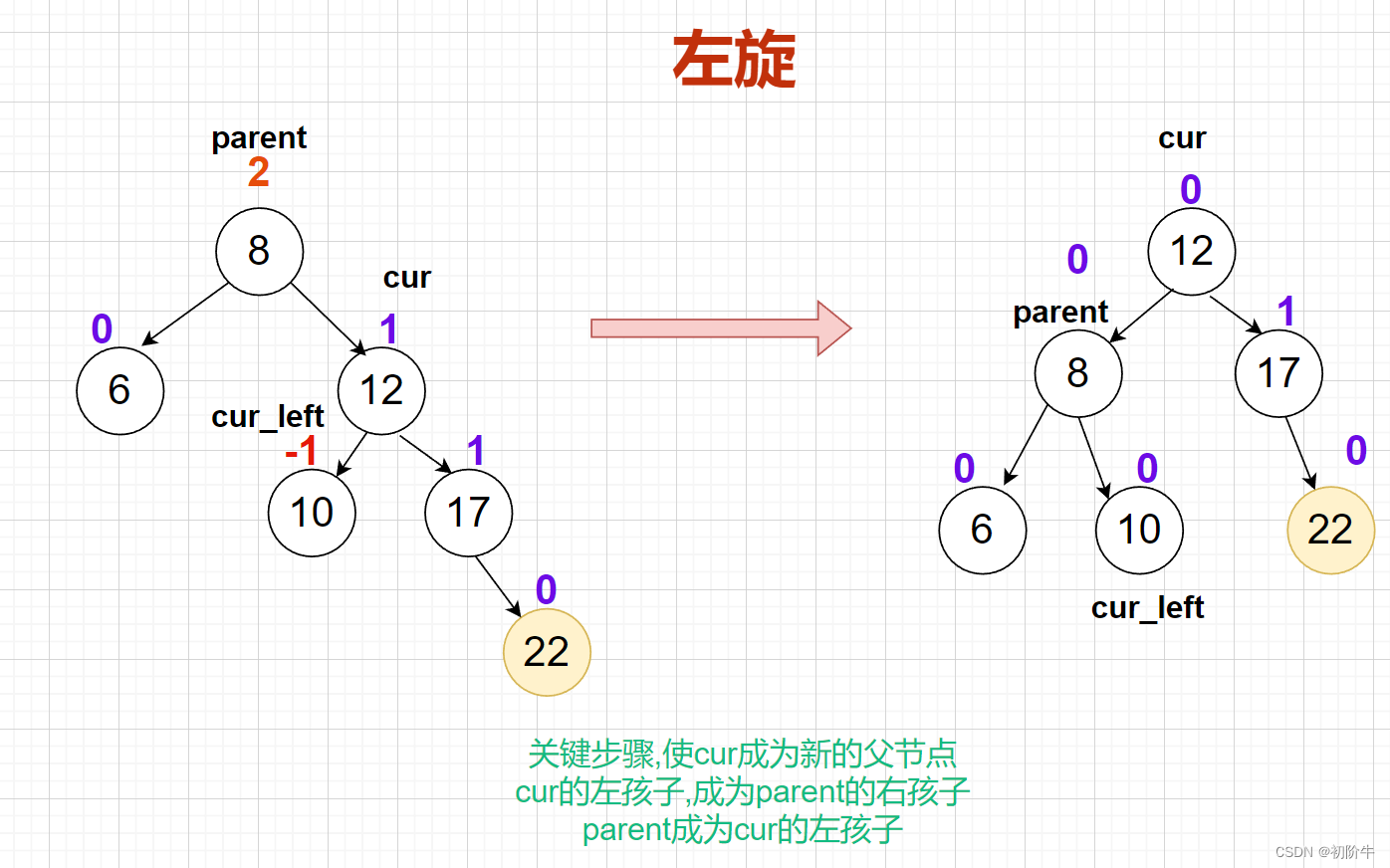
(1)左旋具体图:

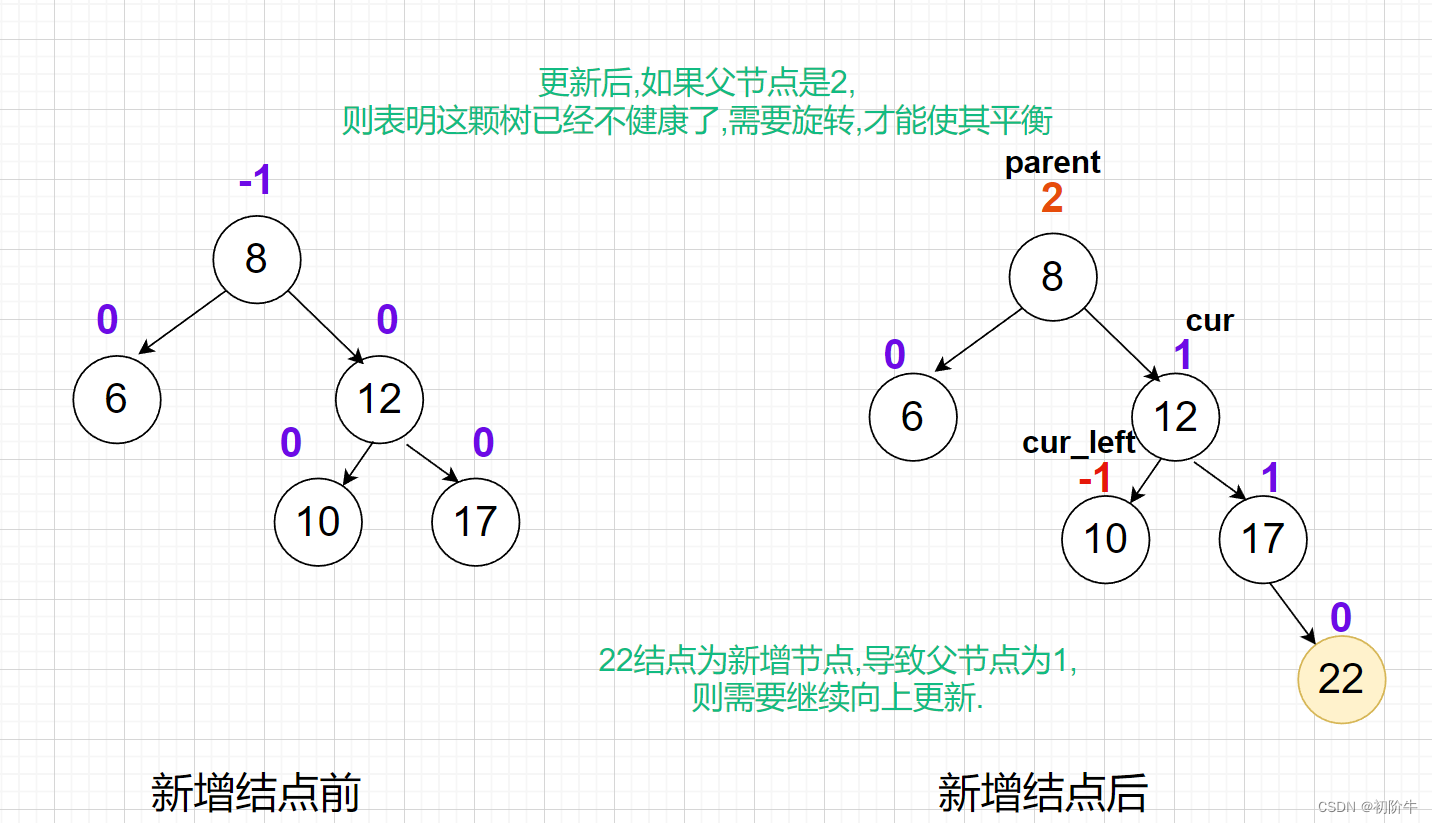
在这里插入图片描述
关键步骤:

使cur成为新的父节点
cur的左孩子,成为parent的右孩子
parent成为cur的左孩子
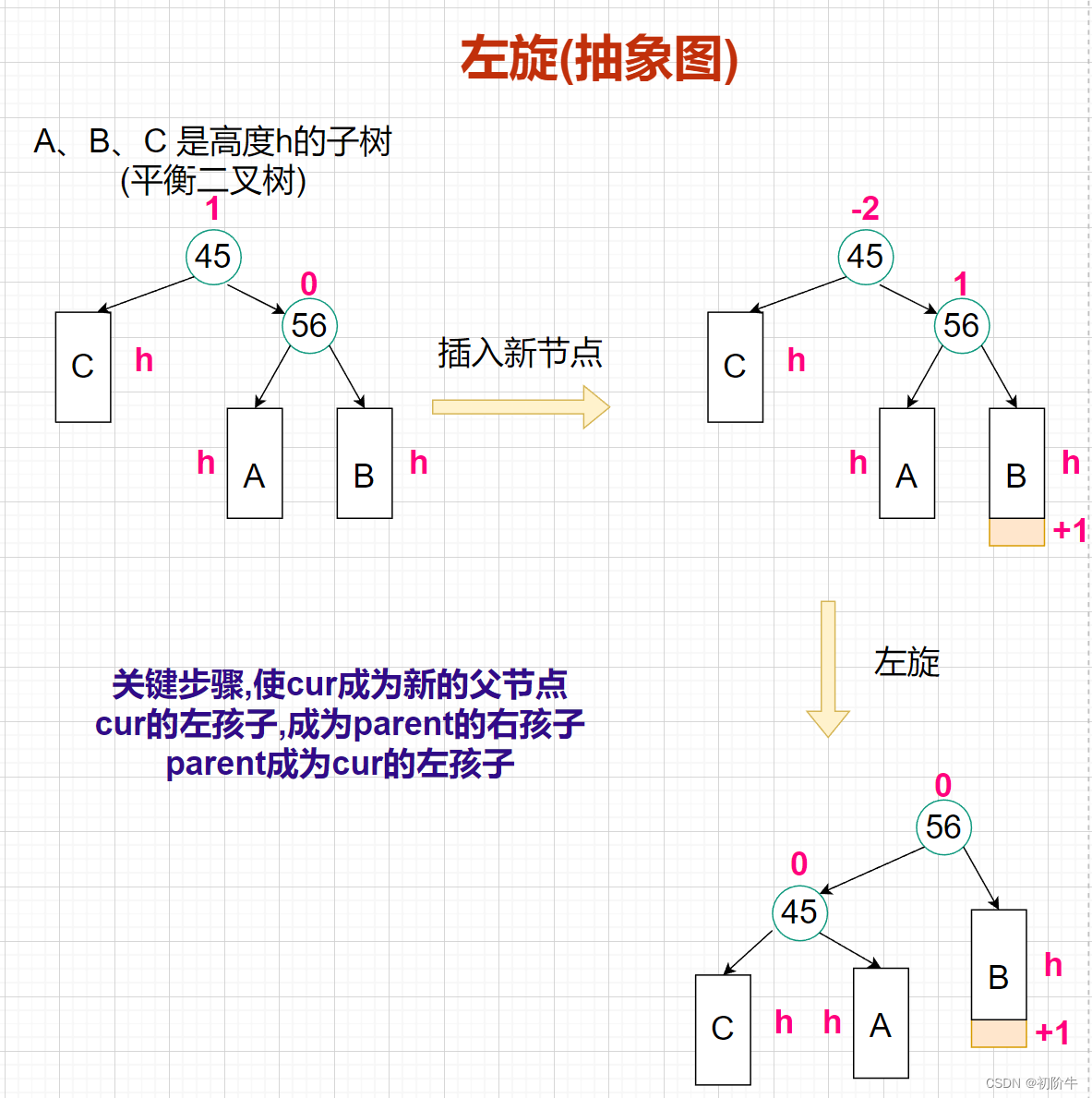
在这里插入图片描述

(2)左旋抽象图

在这里插入图片描述

更新平衡因子:
从抽象图可以看出,左旋旋转后,平衡因子cur parent都可以无脑设置为0.

代码实现:

//左旋
template<class K, class V>
void AVLTree<K, V>::RotateL(Node* parent)
{
	Node* ppnode = parent->_parent;
	Node* cur = parent->_right;
	Node* cur_left = cur->_left;

	//cur的右子树变成parent的左子树
	if (cur_left) {					//cur_right  可能不存在
		parent->_right = cur_left;
		cur_left->_parent = parent;//保持三叉连
	}
	else {
		parent->_right = nullptr;
	}

	//parent变成cur的左子树
	cur->_left = parent;
	parent->_parent = cur;//保持三叉连


	if (ppnode) {
		cur->_parent = ppnode;

		if (ppnode->_left == parent) {		//如果是上面的左子树
			ppnode->_left = cur;
		}
		else {
			ppnode->_right = cur;			//如果是上面的右子树
		}
	}
	else {									//如果ppnode是nullptr,则代表parent为root
		_root = cur;
		cur->_parent = nullptr;
	}
	//更新平衡因子
	parent->_bf = 0;
	cur->_bf = 0;
}

③右左双旋

当cur->_bf 的值是-1，并且parent->_bf 的值是 2，如下图15结点，22结点，18结点这般成折线状。
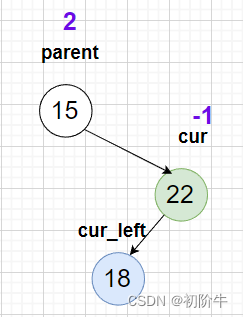
在这里插入图片描述

（1）右左双旋具体图

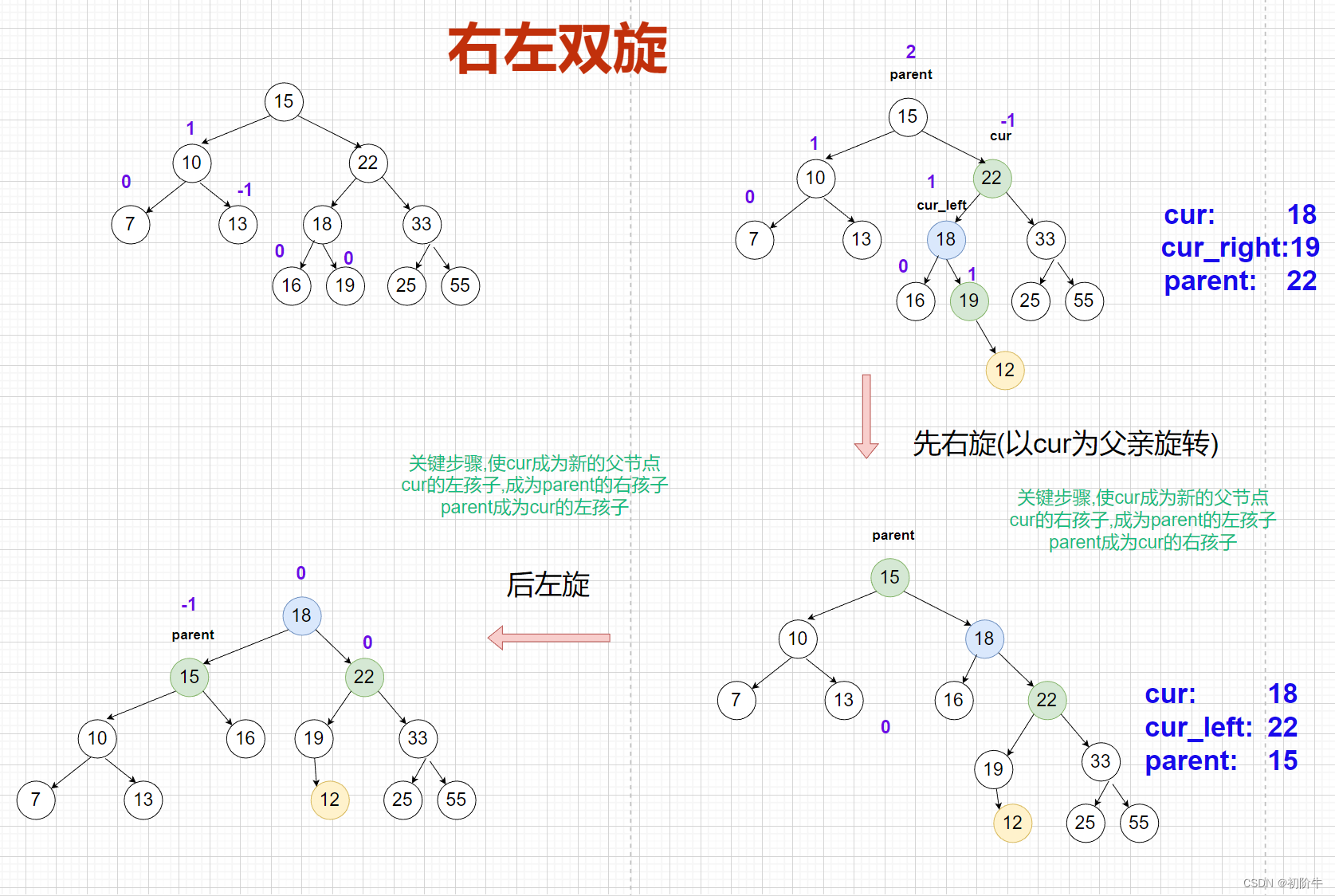
在这里插入图片描述

（2）右左双旋抽象图

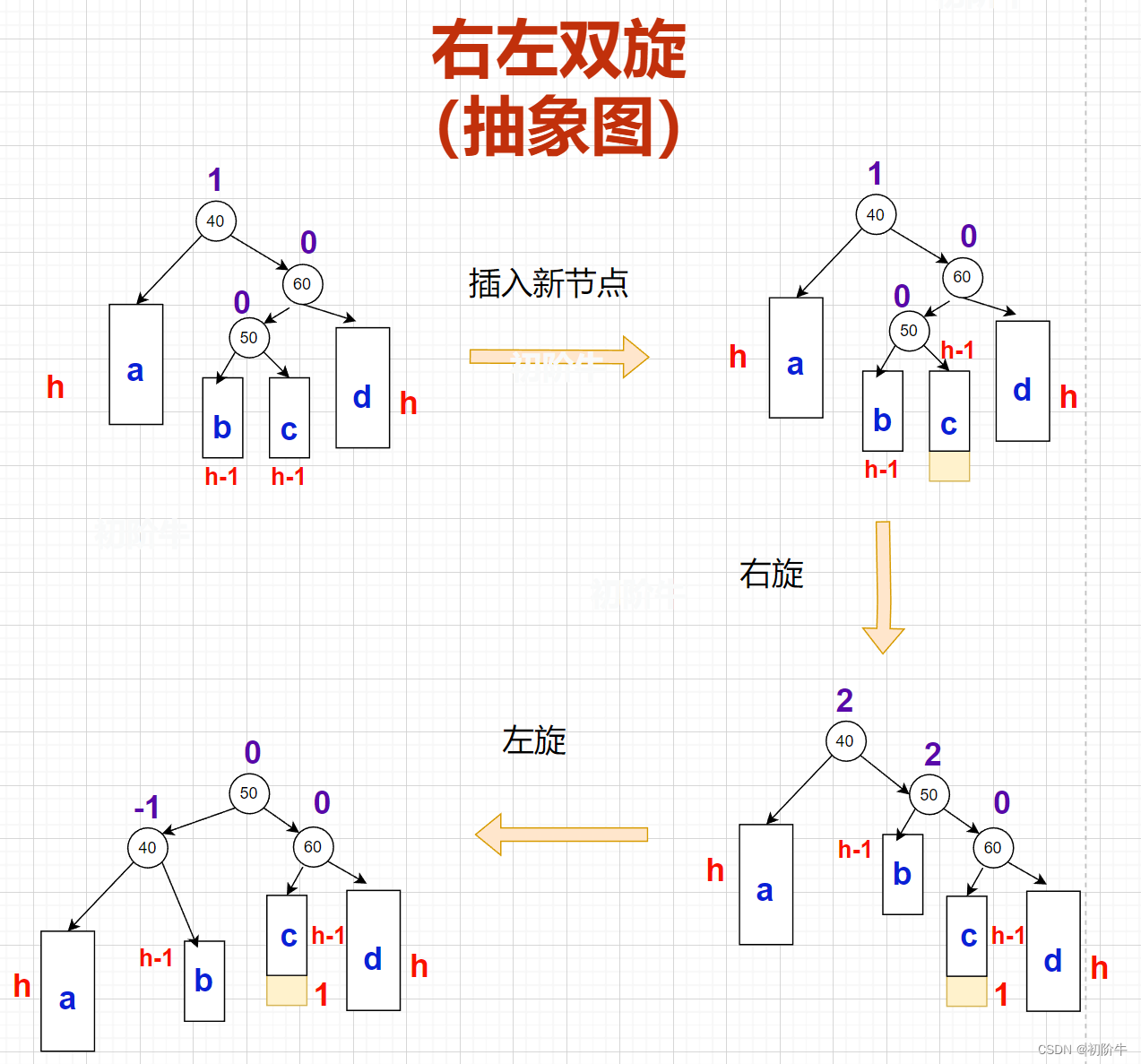
在这里插入图片描述

对于双旋，重点在于如何更新平衡因子。

双旋的重点！！！：
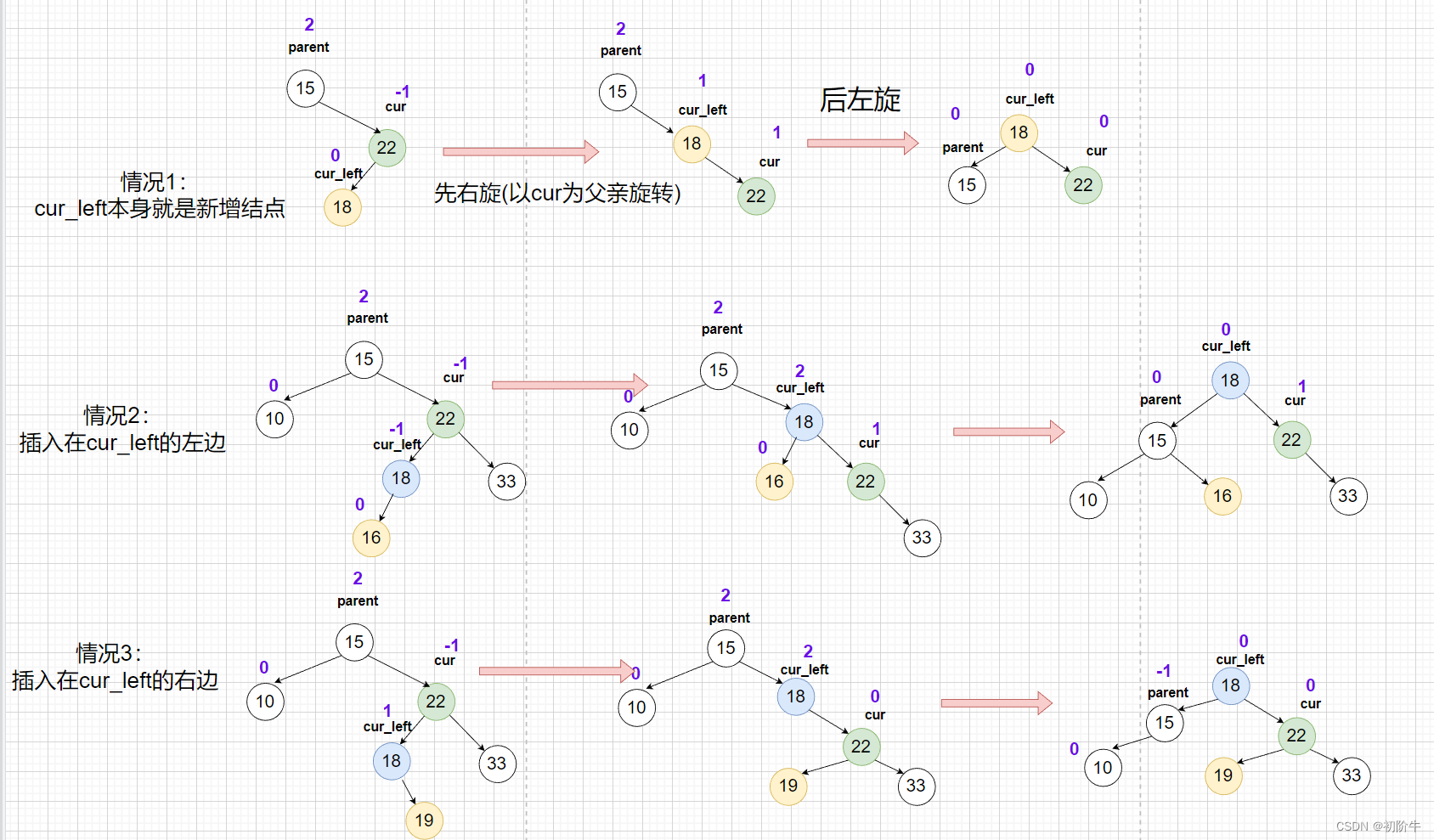
在这里插入图片描述

代码实现:

// 右左双旋

template<class K, class V>
void AVLTree<K, V>::RotateRL(Node* parent) {
	Node* cur = parent->_right;
	Node* cur_left = cur->_left;

	RotateR(cur);			//以parent的right作为新的parent进行右单旋
	RotateL(parent);

	//更新平衡因子(最重要)
	if (cur_left->_bf == 0) {		//情况1
		parent->_bf = 0;
		cur_left->_bf = 0;
		cur->_bf = 0;
	}
	else if(cur_left->_bf == 1) {	//情况3
		parent->_bf = -1;
		cur_left->_bf = 0;
		cur->_bf = 0;
	}
	else if (cur_left->_bf == -1) {	//情况2
		parent->_bf = 0;
		cur_left->_bf = 0;
		cur->_bf = 1;
	}
	else {
		assert(false);
	}
}

④左右双旋

与左右双旋类似，这里不过多介绍了，注意更新平衡因子！！！

（1）左右双旋具体图

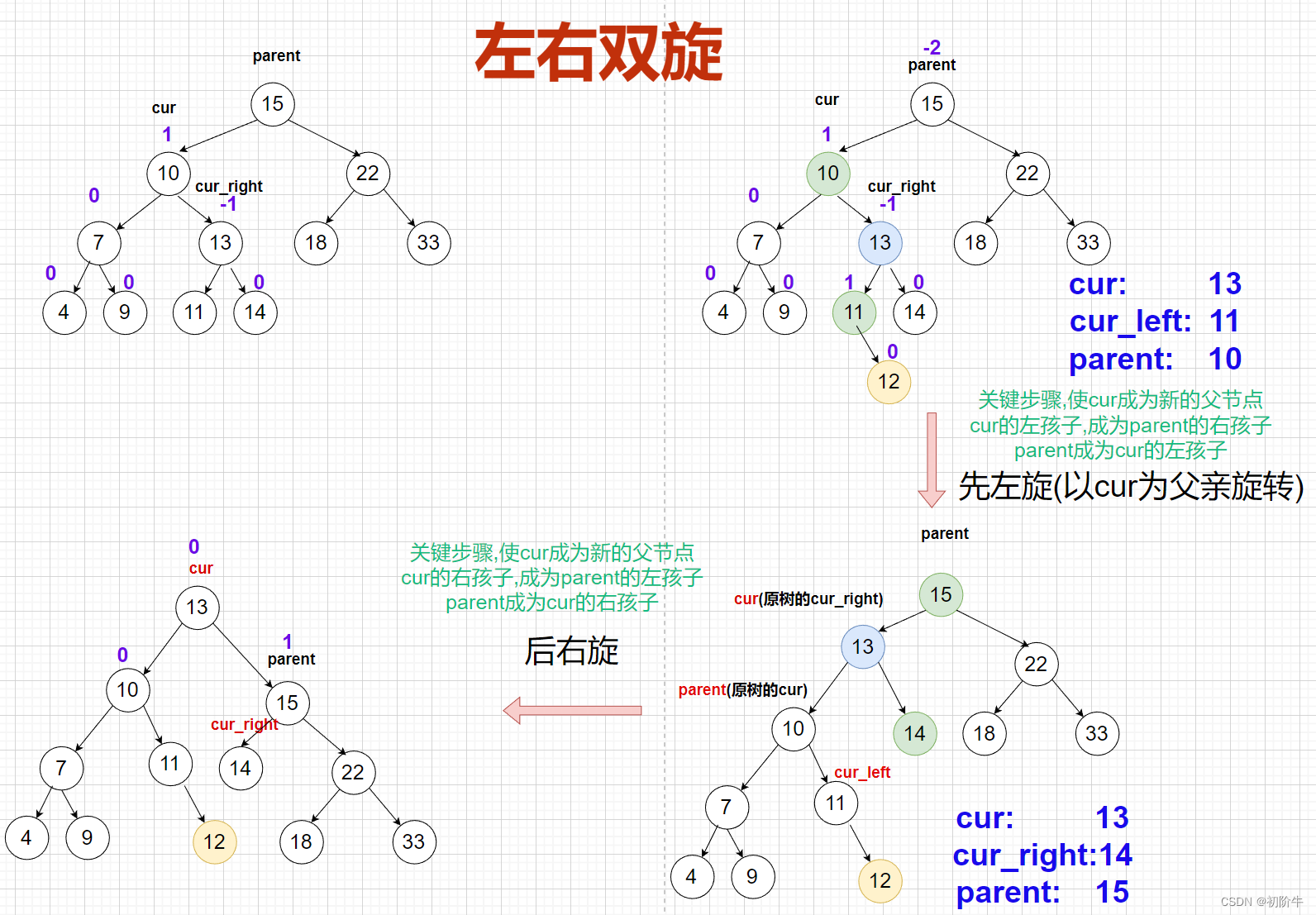
在这里插入图片描述

（2）左右双旋抽象图

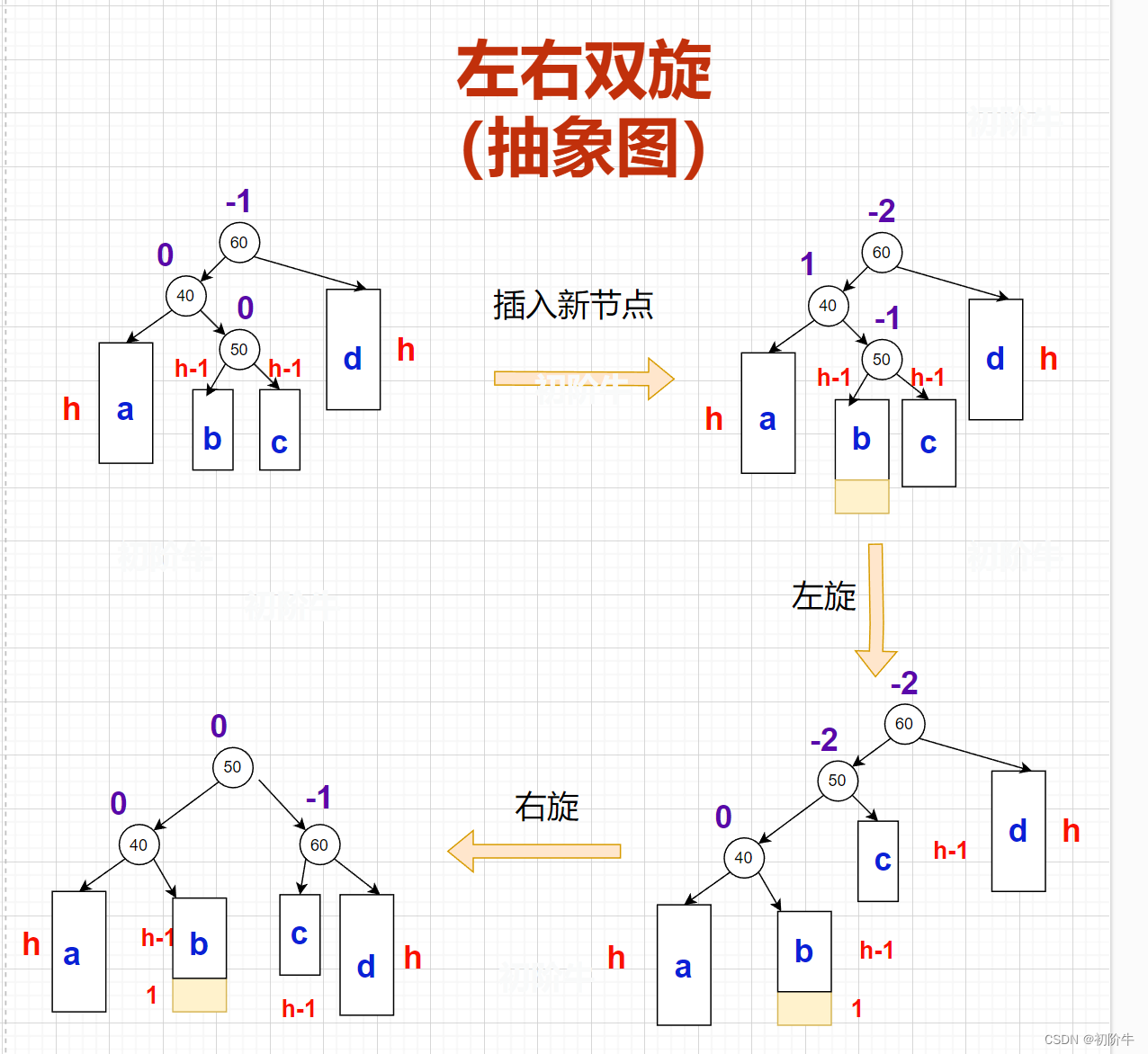
在这里插入图片描述

template<class K, class V>
void AVLTree<K, V>::RotateLR(Node* parent) {
	Node* cur = parent->_left;
	Node* cur_right = cur->_right;

	RotateR(cur);			//以parent的right作为新的parent进行右单旋
	RotateL(parent);

	//更新平衡因子(最重要)
	if (cur_right->_bf == 0) {
		parent->_bf = 0;
		cur_right->_bf = 0;
		cur->_bf = 0;
	}
	else if (cur_right->_bf == 1) {
		parent->_bf = 0;
		cur_right->_bf = 0;
		cur->_bf = -1;
	}
	else if (cur_right->_bf == -1) {
		parent->_bf = 1;
		cur_right->_bf = 0;
		cur->_bf = 0;
	}
	else {
		assert(false);
	}
}

"插入"操作的代码实现:

template<class K,class V>
bool AVLTree<K,V>::Insert(const pair<K, V>& kv)
{
	if (_root == nullptr) {
		_root = new Node(kv);
		return true;
	}

	Node* cur = _root, * parent = nullptr;
	//寻找插入位置
	while (cur) {
		parent = cur;
		if (_root->_kv.first > kv.first) {
			cur = cur->_left;
		}
		else if (_root->_kv.first < kv.first) {
			cur = cur->_right;
		}
		else {
			return false;
		}
	}
	//判断插入在左边还是右边
	cur = new Node(kv);

	if (kv.first < parent->_kv.first){				//插入在左边
		parent->_left = cur;
	}
	else{									//插入在右边
		parent->_right = cur;
	}
	cur->_parent = parent;					//保证三叉链的关系

	//更新平衡因子,最终可能更新到根节点
	while (parent) {							
		if (cur==parent->_left) {			//如果是插入在左边,平衡因子-1
			parent->_bf--;					
		}
		else if(parent->_right == cur) {								//如果是插入在右边,//平衡因子+1
			parent->_bf++;					
		}
		if (parent->_bf == 0) {	//平衡了,很健康,不需要往上调整
			break;
		}
		else if (parent->_bf == -1 || parent->_bf == 1) {	//表明只是有点感冒,还无伤大雅,继续往上更新.
			cur = parent;
			parent = parent->_parent;
		}
		else if (parent->_bf == -2 || parent->_bf == 2) {		//此时已经不平衡了,需要旋转
			//左边高,右单旋
			if (cur->_bf == -1 && parent->_bf == -2) {
				RotateR(parent);
			}else 	if (cur->_bf == 1 && parent->_bf == 2) {	//右边高,左单旋
				RotateL(parent);
			}else 	if (cur->_bf == 1 && parent->_bf == -2) {	//左右双旋
				RotateLR(parent);
			}else 	if (cur->_bf == -1 && parent->_bf == 2) {	//右左双旋
				RotateRL(parent);
			}
		}
	}
	return true;
}

2.2 中序遍历:

由于中序遍历需要传参 参数为根节点，而根节点是私有成员变量，所以这里用再套一层函数的方法，是一个不错的设计。

template<class K, class V>
void  AVLTree<K, V>::_InOrder(Node* root)
{
	if (root == nullptr)return;
	_InOrder(root->_left);
	cout << root->_kv.first << "->" << root->_kv.second << endl;
	_InOrder(root->_right);
}

template<class K, class V>
void  AVLTree<K, V>::InOrder()
{
	if (_root == nullptr)
	{
		cout << "空树" << endl;
		return;
	}
	_InOrder(_root);
}

2.3 AVL树的"高度"

同求二叉树的高度没有啥区别。

需要注意的是：
1处和2处，需要记录左右子树的根否则后面的都需要重新大量的重复计算。


template<class K, class V>
size_t AVLTree<K, V>::_Height(Node* root)
{
	if (root == nullptr)
		return 0;

	int leftHeight = _Height(root->_left);		//1
	int rightHeight = _Height(root->_right);	//2

	return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}

2.4 验证AVL树

判断每棵树的平衡因子是否=右子树-左子树的高度即可。

template<class K, class V>
bool AVLTree<K, V>::_IsAVLTree(Node* root) {
	if (root == nullptr)
		return true;

	int leftHight = _Height(root->_left);
	int rightHight = _Height(root->_right);

	if (rightHight - leftHight != root->_bf)
	{
		cout << "平衡因子异常:" << root->_kv.first << "->" << root->_bf << endl;
		return false;
	}

	return abs(rightHight - leftHight) < 2
		&& _IsAVLTree(root->_left)
		&& _IsAVLTree(root->_right);
}

结语

AVL树的平衡性使得它的插入、删除和查找操作的时间复杂度都是O(logn)，与红黑树相当。然而，由于AVL树在每次插入或删除时都需要进行平衡调整，所以它的常数比红黑树稍大，因此在实际应用中，红黑树更为常用。
后续会更新红黑树的介绍，很多人认为红黑树是比AVL树还要优秀的结构，不想要了解一下吗？ 还请保持关注哦！
在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1319647.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

精选暖心的早安问候语图片，送一份温馨问候、送一串真诚祝福!

精选暖心的早安问候语图片，送一份温馨问候、送一串真诚祝福!

1、寒天催日短&#xff0c;风浪与云平;大雪随风降&#xff0c;祝福与您行;降温总无情&#xff0c;问候暖身心;短信虽礼轻&#xff0c;礼轻情意重!冬季渐深&#xff0c;温度渐冷&#xff0c;注意身体&#xff0c;健康养生!早上好&#xff01; ​ 2、问候是明亮的灯塔&#xff0…
阅读更多...
第二证券：激发资本市场数智新动能 实现高质量发展

第二证券：激发资本市场数智新动能 实现高质量发展

12月15日至16日&#xff0c;深交所与港交所、广期所联合举行主题为“科技引领数智赋能”的2023年大湾区生意所科技大会。 本次大会深化贯彻落实中心经济作业会议精神和中心金融作业会议精神&#xff0c;聚焦工作数字化转型和科技立异前沿趋势&#xff0c;深化粤港澳大湾区协同…
阅读更多...
C语言文件权限

C语言文件权限

前言 提笔不会忘字的人&#xff0c;提键盘却忘了编程语言&#xff0c;差点忘本了&#xff0c;用python&#xff0c;shell等脚本语言忘记C语言怎么用了&#xff0c;研究文件系统简单的文件读写不会写了&#xff0c;记录一下。 简单的文件读写 #include <unistd.h> #inc…
阅读更多...
快猫视频模板源码定制开发 苹果CMS 可打包成双端APP

快猫视频模板源码定制开发 苹果CMS 可打包成双端APP

苹果CMS快猫视频网站模板源码&#xff0c;可用于开发双端APP&#xff0c;后台支持自定义参数&#xff0c;包括会员升级页面、视频、演员、专题、收藏和会员系统等完整模块。还可以直接指定某个分类下的视频为免费专区&#xff0c;具备完善的卡密支付体系&#xff0c;无需人工管…
阅读更多...
Apipost检测接口工具的基本使用方法

Apipost检测接口工具的基本使用方法

&#x1f440; 今天言简意赅的介绍一款和postman一样好用的后端接口测试工具Apipost 专门用于测试后端接口的工具&#xff0c;可以生成接口使用文档官方下载网站&#xff1a;http://www.apipost.cn 傻瓜式安装—>register->项目->创建项目->APIs->新建目录&…
阅读更多...
Spring Boot 3 + Vue 3 整合 WebSocket (STOMP协议) 实现广播和点对点实时消息

Spring Boot 3 + Vue 3 整合 WebSocket (STOMP协议) 实现广播和点对点实时消息

&#x1f680; 作者主页&#xff1a; 有来技术 &#x1f525; 开源项目&#xff1a; youlai-mall &#x1f343; vue3-element-admin &#x1f343; youlai-boot &#x1f33a; 仓库主页&#xff1a; Gitee &#x1f4ab; Github &#x1f4ab; GitCode &#x1f496; 欢迎点赞…
阅读更多...
CTF竞赛密码学题目解析

CTF竞赛密码学题目解析

CTF&#xff08;Capture The Flag&#xff09;竞赛是一个有趣的挑战。密码学是CTF竞赛中的核心元素之一&#xff0c;通常涉及解密、破译密码、理解加密算法等技能。以下是30个题目及答案&#xff0c;新入行的可以看看鸭。 题目及答案 1. Caesar Cipher 描述&#xff1a;给出一…
阅读更多...
MinHash-LSH：如何解决医学大模型的大规模数据去重？

MinHash-LSH：如何解决医学大模型的大规模数据去重？

MinHash-LSH 最小哈希 局部敏感哈希&#xff1a;如何解决医学大模型的大规模数据去重&#xff1f; 大模型的数据问题MinHash-LSH 最小哈希 局部敏感哈希&#xff1a;大规模数据集去重优化Jaccard相似度&#xff1a;用于比较样本集之间的相似性降维技术 MinhashLSH – 局部敏感…
阅读更多...
SCC-Tarjan算法，强连通分量算法，从dfs到Tarjan详解

SCC-Tarjan算法，强连通分量算法，从dfs到Tarjan详解

文章目录 前言定义强连通强连通分量 Tarjan算法原理及实现概念引入搜索树有向边的分类强连通分量的根时间戳追溯值 算法原理从深搜到TarjanTarjan算法流程Tarjan算法代码实现 OJ练习&#xff1a; 前言 强连通分量是图论中的一个重要概念&#xff0c;它在许多领域都有广泛的应用…
阅读更多...
Qt之使用QListView加载相册(富文本ToolTip)

Qt之使用QListView加载相册(富文本ToolTip)

一.效果 二.实现 #include "mainwindow.h" #include "ui_mainwindow.h"#include <QStandardItemModel> #include <QFont>MainWindow::MainWindow(QWidget *parent): QMainWindow(parent), ui(new Ui::MainWindow) {ui->setupUi(this);QFont…
阅读更多...
SourceTree 免登录跳过初始设置

SourceTree 免登录跳过初始设置

用于Windows和Mac的免费Git客户端。 Sourcetree简化了如何与Git存储库进行交互&#xff0c;这样您就可以集中精力编写代码。通过Sourcetree的简单Git GUI可视化和管理存储库。 SourceTree 安装之后需要使用账号登陆以授权&#xff0c;以前是可以不登陆的&#xff0c;但是现在是…
阅读更多...
基于ssm办公自动化管理系统论文

基于ssm办公自动化管理系统论文

摘 要 随着计算机应用的普及、成熟&#xff0c;越来越多公司开始采用网上信息管理系统&#xff0c;网上信息管理系统的运行可以有效的提高企业管理效率。因此&#xff0c;为满足企业办公管理方面的需求&#xff0c;开发了办公自动化管理系统。 本文重点阐述了办公自动化管理系…
阅读更多...
c语言：输出1～100的数据以10×10格式

c语言：输出1～100的数据以10×10格式

一、题目 以10*10的格式&#xff0c;输出1-100。 如图&#xff1a; 二、思路分析 此题的难点&#xff1a; 1、1-9的要向前空一格&#xff1b; 2、100要向前进一格 三、代码截图【带注释】 四、源代码【带注释】 #include <stdio.h> int main() { //分成三个部分&am…
阅读更多...
Axure的交互与情形，事件，动作

Axure的交互与情形，事件，动作

交互样式 交互样式是指当用户与原型进行交互时&#xff0c;元素所呈现出的视觉效果。在Axure中&#xff0c;可以通过设置交互样式来调整元素在交互过程中的外观&#xff0c;例如改变颜色、大小、位置等。 交互事件 交互事件是指在用户与原型进行交互时触发的动作。在Axure中&…
阅读更多...
计算机图形学头歌合集（题集附解）

计算机图形学头歌合集（题集附解）

目录 CG1-v1.0-点和直线的绘制 第1关&#xff1a;OpenGL点的绘制 第2关&#xff1a;OpenGL简单图形绘制 第3关&#xff1a;OpenGL直线绘制 第4关&#xff1a;0<1直线绘制-dda算法<> 第5关&#xff1a;0<1直线绘制-中点算法<> 第6关&#xff1a;一般直线绘…
阅读更多...
使用Log4j与log4j2配置mybatisplus打印sql日志

使用Log4j与log4j2配置mybatisplus打印sql日志

环境&#xff1a;项目非完全spring项目&#xff0c;没有spring的配置文件。执行sql时老是不打印sql语句。因此进行修改&#xff0c;过程比较坎坷&#xff0c;记录一下。 我尝试使用log4j和log4j2进行配置 最终把这两种全部配置记录上 Log4j配置 如果项目用的是log4j需要进行配置…
阅读更多...
nodejs配置express服务器，运行自动打开浏览器

nodejs配置express服务器，运行自动打开浏览器

查看专栏目录 Network 灰鸽宝典专栏主要关注服务器的配置&#xff0c;前后端开发环境的配置&#xff0c;编辑器的配置&#xff0c;网络服务的配置&#xff0c;网络命令的应用与配置&#xff0c;windows常见问题的解决等。 文章目录 设置方法&#xff1a;1&#xff0c;安装nodej…
阅读更多...
全国软件供应链安全产教融合共同体成立大会在武汉成功举办

全国软件供应链安全产教融合共同体成立大会在武汉成功举办

为深入学习贯彻党的二十大精神&#xff0c;落实《关于深化现代职业教育体系建设改革的意见》等要求&#xff0c;探索职业教育产教融合创新发展新生态&#xff0c;培养软件供应链安全人才体系&#xff0c;推动教育链、人才链、产业链、创新链的协同发展&#xff0c;12月16日 &am…
阅读更多...
Spring 6（二）【IOC原理】

Spring 6（二）【IOC原理】

前言 IOC 是Spring的两大核心概念之一&#xff0c;它是一种思想&#xff0c;需要极其熟练的掌握。 今日摘录&#xff1a; 低能无聊的人太多。说他们勤勉&#xff0c;不过是因困为不会合理分配时间&#xff1b;说他们积极&#xff0c;不过是逃避其他困难工作而已。即便说工作只…
阅读更多...
20个CobaltStrike实战案例 +插件

20个CobaltStrike实战案例 +插件

案例 1&#xff1a;窃取 token&#xff0c;访问域控或者本地管理员 前提&#xff1a;1.cs 上线的主机要管理员权限 注意点&#xff1a;登录失败时一定要先恢复身份 方式一&#xff1a; Ps #查看进程 steal_token 2020(管理元权限运行的进程号) &#xff0c; shell dir \\dc\c…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023