前言

强连通分量是图论中的一个重要概念，它在许多领域都有广泛的应用，如网络路由中识别环路，社交网络分析，编译器优化识别出代码中的循环结构，图像处理中识别出图像中的连通区域，从而进行图像分割和特征提取等。因而了解强连通分量的概念以及其求解算法是十分重要的。我们本文介绍Tarjan算法，Tarjan算法在双连通分量求解中也有应用，我们后续博客中也会介绍。

---

定义

强连通

若一张有向图的节点两两互相可达，则称这张图是**强连通(SC,strongly connected)**的。

强连通分量

强连通分量(Strongly Connected Components, SCC): 极大的强连通子图。
如下图中G1 = {1,2,3,4,9} 和 G2 = {5,6,8} 以及 G3 = {7}就是三个强连通分量。

Tarjan算法原理及实现

概念引入

搜索树

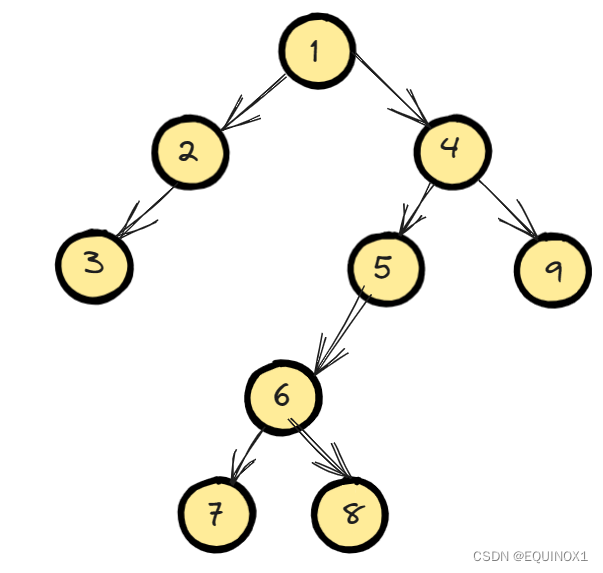
我们dfs对图遍历，保证每个点只访问一次，访问过的节点和边构成一棵有向树，我们称之为搜索树。

如我们上图从1开始深搜遍历就会得到如下搜索树。

有向边的分类

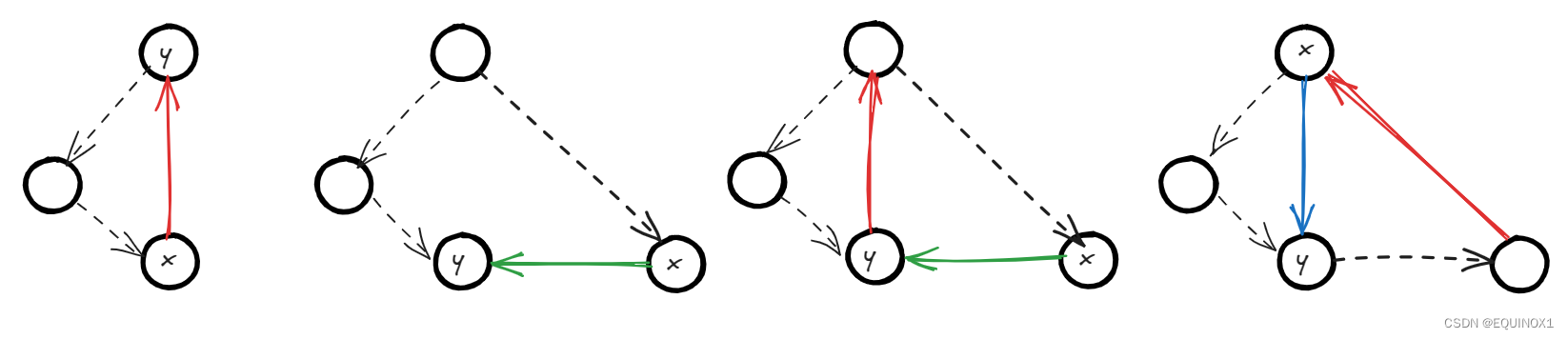
深搜对于有向边的访问分为四类：

1.树边(tree edge):访问节点走过的边。图中的黑色边。
2.返祖边(back edge):指向祖先节点的边。图中的红色边。
3.横叉边(cross edge):右子树指向左子树的边。图中的绿色边。.
4.前向边(forward edge):指向子树中节点的边。图中的蓝色边。

我们不难发现返祖边必和树边构成环。横叉边可能和返祖边构成环。

前向边无用，因为前向边如果作为某个环中的边，必有一个更大的环替代该环。

强连通分量的根

如果节点x是某个强连通分量在搜索树中遇到的第一个节点，那么这个强连通分量的其余节点肯定是在搜索树中以x为根的子树中。节点x被称为这个强连通分量的根。

时间戳

我们用数组dfn[]来保存节点第一次访问时间，dfn[x]即节点x第一次访问的时间戳。

追溯值

数组low[]来记录每个节点出发能够访问的最早时间戳，记low[x]节点x出发能够访问的最早时间戳，即追溯值。

算法原理

从深搜到Tarjan

Tarjan算法通过记录深搜遍历中每个节点的第一次访问时间来找到强连通分量的根以及其余节点。

前面已经讲了Tarjan是基于深搜的，所以我们的Tarjan实际上是在深搜遍历图的模板上加以修改而实现的。

我们先给出链式前向星存图的深搜代码。（关于链式前向星，详见：一种实用的边的存储结构–链式前向星-CSDN博客）

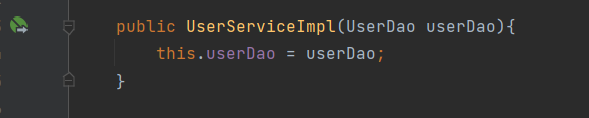
void tarjan(int x)//深搜模板
{
    //链式前向星存图
    for (int j = head[x]; ~j; j = edges[j].nxt)
    {
    	int v = edges[j].v;
    	if(vis[v]) continue;
    	vis[v] = 1;
    	tarjan(v);
    }
}

即然Tarjan算法是跟时间戳和追溯值有关的，我们如何在深搜过程中完成对二者的记录呢？

我们用全局变量tot来记录时间，由于上面深搜代码保证了进入函数的都是未访问即第一次访问的节点，所以我们进入函数体的时候记录dfn[x]为++tot，并初始化low[x]为dfn[x]，则有如下代码

void tarjan(int x)//深搜模板
{
    dfn[x] = low[x] = ++tot;
    for (int j = head[x]; ~j; j = edges[j].nxt)
    {
    	int v = edges[j].v;
    	if(vis[v]) continue;
    	vis[v] = 1;
    	tarjan(v);
    }
}

对于dfn的值是无可指摘的，但是对于非强连通分量根节点x的low值显然不是dfn[x]，那么我们如何在遍历过程中去维护low呢？

如果相邻节点v未访问，那么我们先对v深搜，然后用v的low值更新low[x]

如果已经访问过了，直接用v的low值更新low[x]，则有

void tarjan(int x)//深搜模板
{
    dfn[x] = low[x] = ++tot;
    for (int j = head[x]; ~j; j = edges[j].nxt)
    {
        int v = edges[j].v;
        if (!dfn[v])//预先初始化的dfn全为0，时间戳为0说明还未访问
        {
            tarjan(v);
            low[x] = min(low[x], low[v]);
        }
        else
        {
            low[x] = min(low[x], low[v]);
        }
    }
}

我们现在似乎只是完成了深搜遍历图以及记录dfn和low罢了，还没有真正的涉及到强连通分量的求解。

对于一个强连通分量的根来讲，当它的访问完毕后，它所在的强连通分量所有节点必然都已经访问过，也就是说我们需要从根的时间戳往后的访问节点中找到其强连通分量内的其他点。

这就要求我们用一个数据结构来存储访问过的点，这里我们选择使用栈，因为这样能保证先访问的在栈底，强连通分量中后访问的节点在栈中位置都在根节点上方，而我们如何判断根呢？我们知道根是所在强连通分量第一个访问的点，所以一定满足dfn[root] == low[root]

我们回看最初的图和搜索树

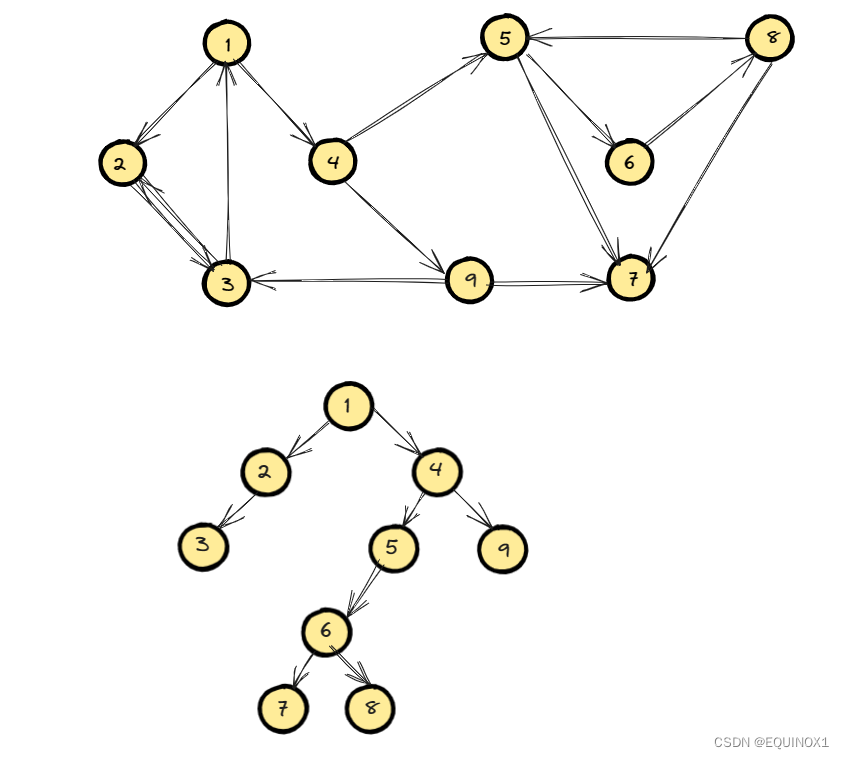
我们在深搜的过程中标记时间戳的同时将节点入栈，那么我们按照搜索树往下走：

• 发现最先访问完的节点是3，此时栈中元素为{1，2，3}，我们结合原图来看发现1，2，3在一个强连通分量内，但是由于3不是根，不能保证所在强连通分量遍历完了，所以不做操作
• 接下来2遍历完了，和3一样，不做操作。
• 回到1后，接着从4往下遍历。到7的时候，7又成为了访问完的节点，我们发现dfn[7] == low[7] = 7，所以7是其所在强连通分量的根，其所在强连通分量其它点都在栈中，我们发现7在栈顶，所以7所在的强连通分量只有7，到此我们将7弹栈
• 接着遍历，此时到8的时候又发现8也访问完了，由于8不是根，所以不操作，这样一直下去回到了5，我们发现dfn[5] == low[5] = 5，所以5是其所在强连通分量的根，其所在强连通分量其它点都在栈中，我们此时可以发现栈中5之上的正好是其所在强连通分量内的其他点，因为之前我们已经将7弹栈了，这样我们又处理了5所在强连通分量{5，6，8}
• 接着往下走，我们仿照先前的步骤，又得到了强连通分量{1，2，3，4，9}
• 至此所有强连通分量已经得到：{1，2，3，4，9}，{5，6，8}，{7}

所以我们可以发现，时间戳dfn和追溯值low可以帮我们判定强连通分量的根，从而从栈中拿出其所在强连通分量的节点，且先访问完的强连通分量已经弹栈，不会对后访问完的强连通分量造成影响（更严格的证明可以用反证法自己试着证明一下）。

而且我们也发现一点，由于low值只跟自己强连通分量内点的low值有关，所以我们上面深搜代码中维护low值的部分第二个分支判断可改为在栈中，因为如果不在栈中而且访问过了说明它所在的强连通分量已经解决了，跟当前点无关。如下：

        if (!dfn[v])//预先初始化的dfn全为0，时间戳为0说明还未访问
        {
            tarjan(v);
            low[x] = min(low[x], low[v]);
        }
        else if(instk[v]
        {
            low[x] = min(low[x], low[v]);
        }

Tarjan算法流程

我们到这里就可以得出Tarjan的算法流程：

1. 访问x时，给时间戳、初始化low、入栈。枚举x的邻点v，分三种情况。
2. 若v尚未访问：对v深搜。回x时，用low[v]更新low[x]。因为x是v的父节点，v能访问到的点，x也一定也能访问到
3. 若v已访问且在栈中：说明y是祖先节点或左子树节点，用dfn[v]更新low[x]。（注意，和我们前面分析流程不一样了）
4. 若v已访问且不在栈中：说明v已搜索完毕，其所在连通分量已被处理，所以不用对其做操作。
5. 离x时，记录SCC。只有遍历完一个SCC， 才可以出栈。更新low值的意义：避免SCC的节点提前出栈。

注意我们前面一直讲用low[v]更新low[x]，但是上面流程中用了dfn[v]来更新，如果换成low[v]的话可以负责的讲在SCC问题中绝对正确，但是如果是无向图的双连通分量问题就会出错了，这个和割点有关，后续再写另一篇博客介绍。

Tarjan算法代码实现

#define N 10010
#define M 50010
struct edge
{
    int v, nxt;
} edges[M];
int head[N]{0}, idx = 0;
void addedge(int u, int v)
{
    edges[idx] = {v, head[u]};
    head[u] = idx++;
}
int dfn[N]{0}, low[N]{0}, tot = 0; // tot访问节点的时间戳编号
// dfn 时间戳 low节点所能访问的最小时间戳 tot数目
int s[N], top = 0; // 辅助栈
bitset<N> instk;   // 在栈内？
int scc[N], sz[N], cnt = 0;
// scc 节点所在SCC的编号 sz SCC的大小 cntscc数目
int ans = 0;
void tarjan(int x)
{
    dfn[x] = low[x] = ++tot;
    s[top++] = x, instk[x] = 1;
    for (int j = head[x]; ~j; j = edges[j].nxt)
    {
        if (!dfn[edges[j].v])
        {
            tarjan(edges[j].v);
            low[x] = min(low[x], low[edges[j].v]);
        }
        else if (instk[edges[j].v])
        {
            // y要么是祖先要么是横叉边的点
            // 计算强连通dfn可以换成low，但是在计算双连通替换会出错
            low[x] = min(low[x], dfn[edges[j].v]);
        }
    }
    if (low[x] == dfn[x])
    {
        int y;
        cnt++;
        do
        {
            y = s[--top];
            instk[y] = 0;
            scc[y] = cnt;
            sz[cnt]++;
        } while (x != y);
    }
}

OJ练习：

P2863 [USACO06JAN] The Cow Prom S