一、简介
最近在做一个点云的项目,姿态的变换是一个很重要的环节,从数学上需要彻底理解这些东西之前一直在使用,但是没有系统的总结过,接着2023年元旦的三天时间好好学习一下,然后在同事面前说自己是数学系的很丢人啊。这几天打算从下面几个方向上来做
1、旋转平移矩阵(2D和3D)
2、欧拉角
3、欧拉角和四元数的转换
4、SVD 矩阵分解
5、矩阵的伪逆
6、罗德里格斯公式
非常感谢这位老兄的博客,我们就是学习
旋转变换(一)旋转矩阵_csxiaoshui的博客-CSDN博客_旋转矩阵
二、2D旋转
1、旋转原理推导
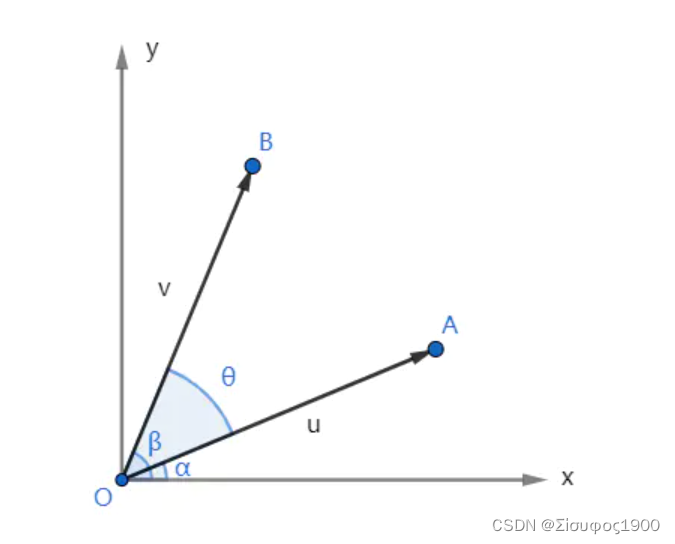
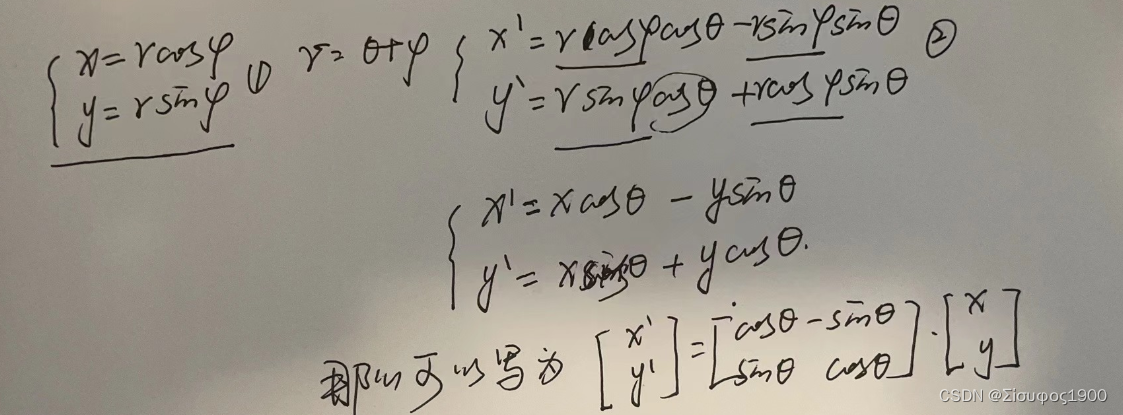
2、绕着一个定点旋转
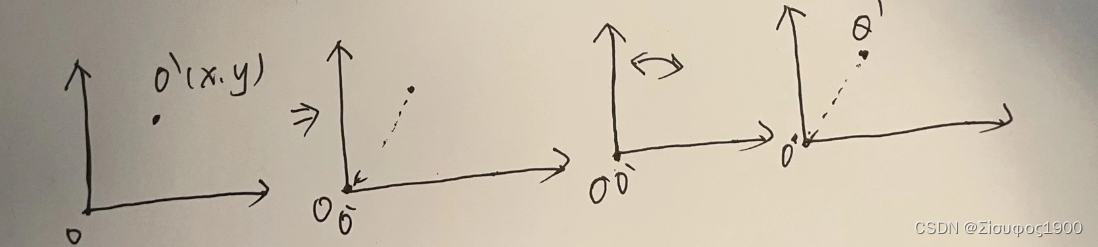
上面说的是绕着原点O 来旋转的,那么如何将绕着一个定点R(x,y)来旋转呢,有如下步骤
1、将R点移动到原点O的位置
平移矩阵如下:
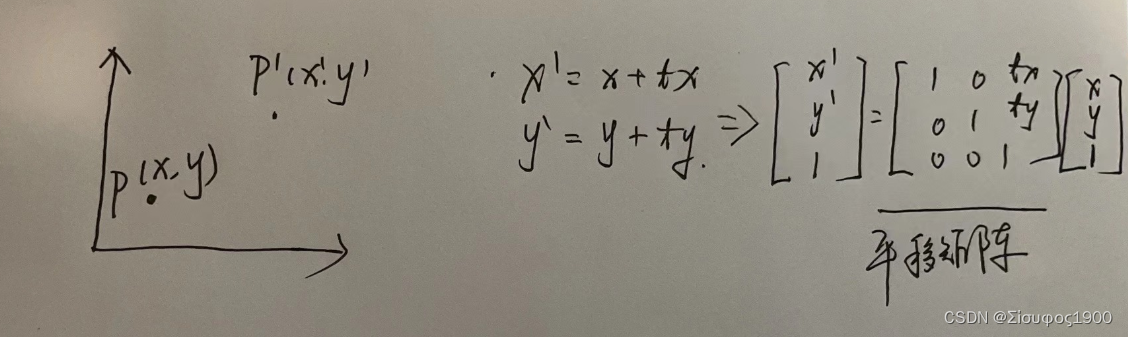
2、绕着原点旋转
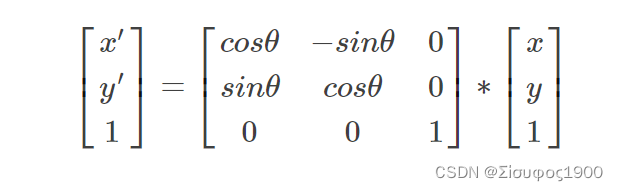
3、将第一步平移的步骤也平移到原来的地方

那么最后的矩阵就是:
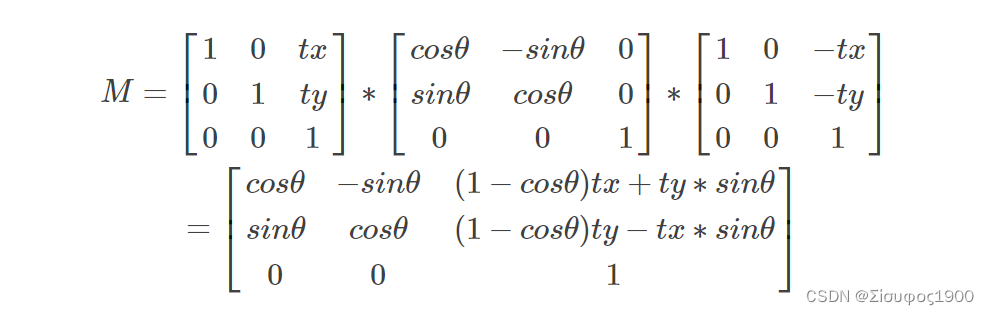
若绕着(2,2)点旋转angle=1/6*pi,
matlab 验证:
>> A=[1 0 2;0 1 2;0 0 1]
A =
1 0 2
0 1 2
0 0 1
>> a=[1 0 -2;0 1 -2;0 0 1]
a =
1 0 -2
0 1 -2
0 0 1
>> R=[cos(1/6*pi) -sin(1/6*pi) 0;sin(1/6*pi) cos(1/6*pi) 0;0 0 1]
R =
0.8660 -0.5000 0
0.5000 0.8660 0
0 0 1.0000
>> M =A*R*a
M =
0.8660 -0.5000 1.2679
0.5000 0.8660 -0.7321
0 0 1.0000
>> 三、3D旋转
1、绕着x 轴旋转
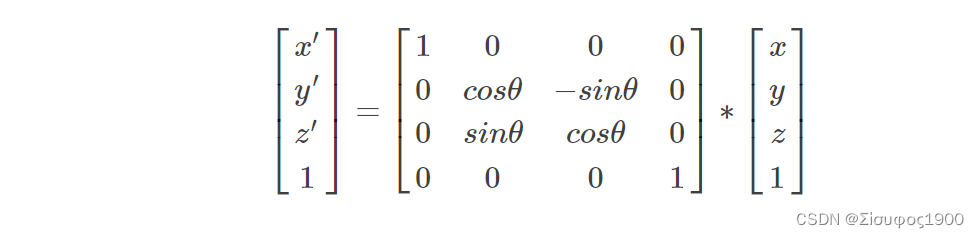
2、绕着y 轴旋转
绕着y轴旋转,其平面是ZOX平面
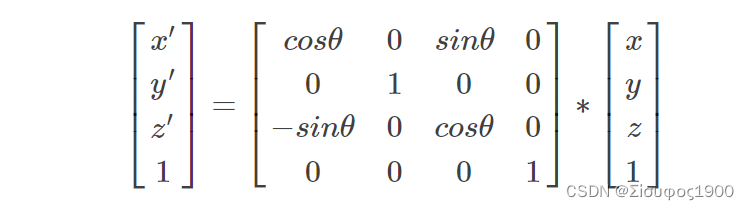
3、绕着z 轴旋转
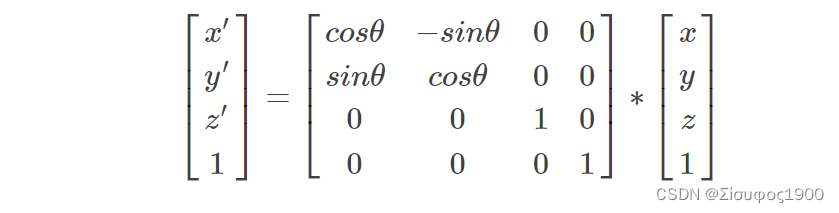
记得在halcon中是旋转的顺序有大概12中之多,通常来说xyz和xyz以及zxy 的矩阵是不一样的,这里我们能使用matlab做个测试
angle=1/6*pi:
Rx=[1 0 0 0 ;
0 cos(1/6*pi) -sin(1/6*pi) 0;
0 sin(1/6*pi) cos(1/6*pi) 0;
0 0 0 1]
Ry=[cos(1/6*pi) 0 sin(1/6*pi) 0;
0 1 0 0 ;
-sin(1/6*pi) 0 cos(1/6*pi) 0;
0 0 0 1]
Rz=[cos(1/6*pi) -sin(1/6*pi) 0 0;
sin(1/6*pi) cos(1/6*pi) 0 0 ;
0 0 1 0;
0 0 0 1]>> Rx=[1 0 0 0 ;0 cos(1/6*pi) -sin(1/6*pi) 0;0 sin(1/6*pi) cos(1/6*pi) 0;0 0 0 1]
Rx =
1.0000 0 0 0
0 0.8660 -0.5000 0
0 0.5000 0.8660 0
0 0 0 1.0000
>> Ry=[cos(1/6*pi) 0 sin(1/6*pi) 0; 0 1 0 0 ;-sin(1/6*pi) 0 cos(1/6*pi) 0;0 0 0 1]
Ry =
0.8660 0 0.5000 0
0 1.0000 0 0
-0.5000 0 0.8660 0
0 0 0 1.0000
>> Rz=[cos(1/6*pi) -sin(1/6*pi) 0 0;sin(1/6*pi) cos(1/6*pi) 0 0 ;0 0 1 0;0 0 0 1]
Rz =
0.8660 -0.5000 0 0
0.5000 0.8660 0 0
0 0 1.0000 0
0 0 0 1.0000
C++程序:
Eigen::Matrix4f RotateMatrix3D(int axis,float angle)
{
// 使用eigen 定义一个单位矩阵
Eigen::Matrix4f _rotateMatrix = Eigen::Matrix4f::Identity();
angle = angle / M_1_PI / 180;
switch (axis)
{
case 0: // 绕着x轴旋转
_rotateMatrix(1, 1) = cos(angle);
_rotateMatrix(1, 2) = -sin(angle);
_rotateMatrix(2, 1) = sin(angle);
_rotateMatrix(2, 2) = -cos(angle);
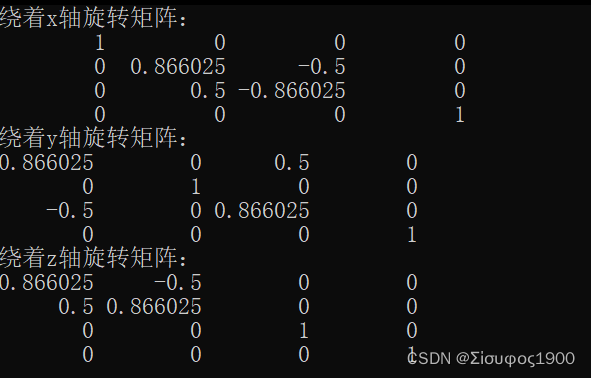
cout << "绕着x轴旋转矩阵: " << endl;
cout << _rotateMatrix << endl;
break;
case 1: // 绕着x轴旋转
_rotateMatrix(0, 0) = cos(angle );
_rotateMatrix(0, 2) = sin(angle );
_rotateMatrix(2, 0) = -sin(angle );
_rotateMatrix(2, 2) = cos(angle );
cout << "绕着y轴旋转矩阵: " << endl;
cout << _rotateMatrix << endl;
break;
case 2:
_rotateMatrix(0, 0) = cos(angle );
_rotateMatrix(0, 1) = -sin(angle );
_rotateMatrix(1, 0) = sin(angle);
_rotateMatrix(1, 1) = cos(angle );
cout << "绕着z轴旋转矩阵: " << endl;
cout << _rotateMatrix << endl;
break;
default:
break;
}
return _rotateMatrix;
}
四、3D绕任意轴旋转
绕任意轴旋转,我们可以将这个旋转分解为一些基本的旋转,然后旋转,案例如下:
我们将绕着U轴从P点旋转到Q点,求出Q点的坐标:
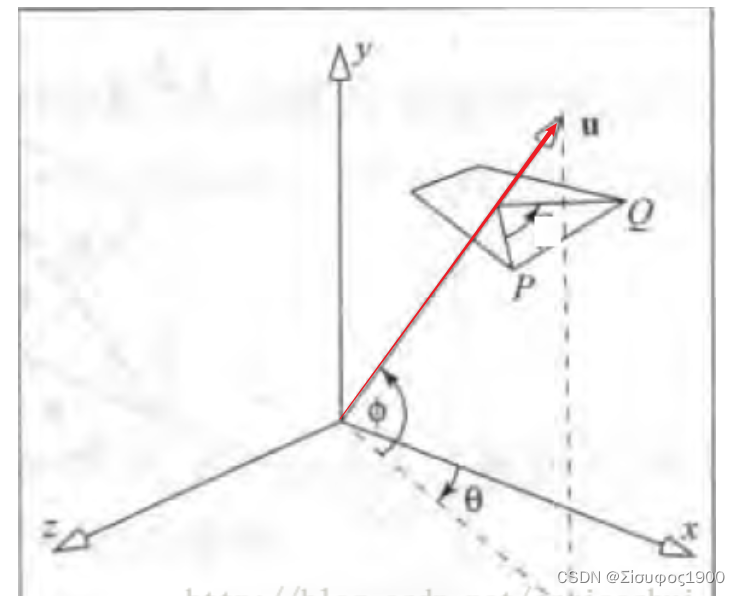
1、