算法设计与分析复习03：动态规划算法

news2024/9/24 9:25:18

算法设计与分析复习03：动态规划算法

文章目录

  • 算法设计与分析复习03：动态规划算法
    • 复习重点
    • 动态规划算法
      • 斐波那契数列及其应用
      • 矩阵链乘法+凸多边形剖分
        • 矩阵链乘法
        • 凸多边形剖分
      • 最长公共子序列
      • 最大子段和（字数组）
      • 0-1背包
      • 编辑距离
      • 钢条切割

复习重点

在这里插入图片描述

动态规划算法

斐波那契数列及其应用

在这里插入图片描述
在这里插入图片描述
时间复杂度为 O ( 2 n ) O(2^n) O(2n)，随问题规模，呈指数级别增加。
在这里插入图片描述
记忆化搜索的时间复杂度为 O ( n ) O(n) O(n)。
在这里插入图片描述
动态规划的时间复杂度也为 O ( n ) O(n) O(n)。
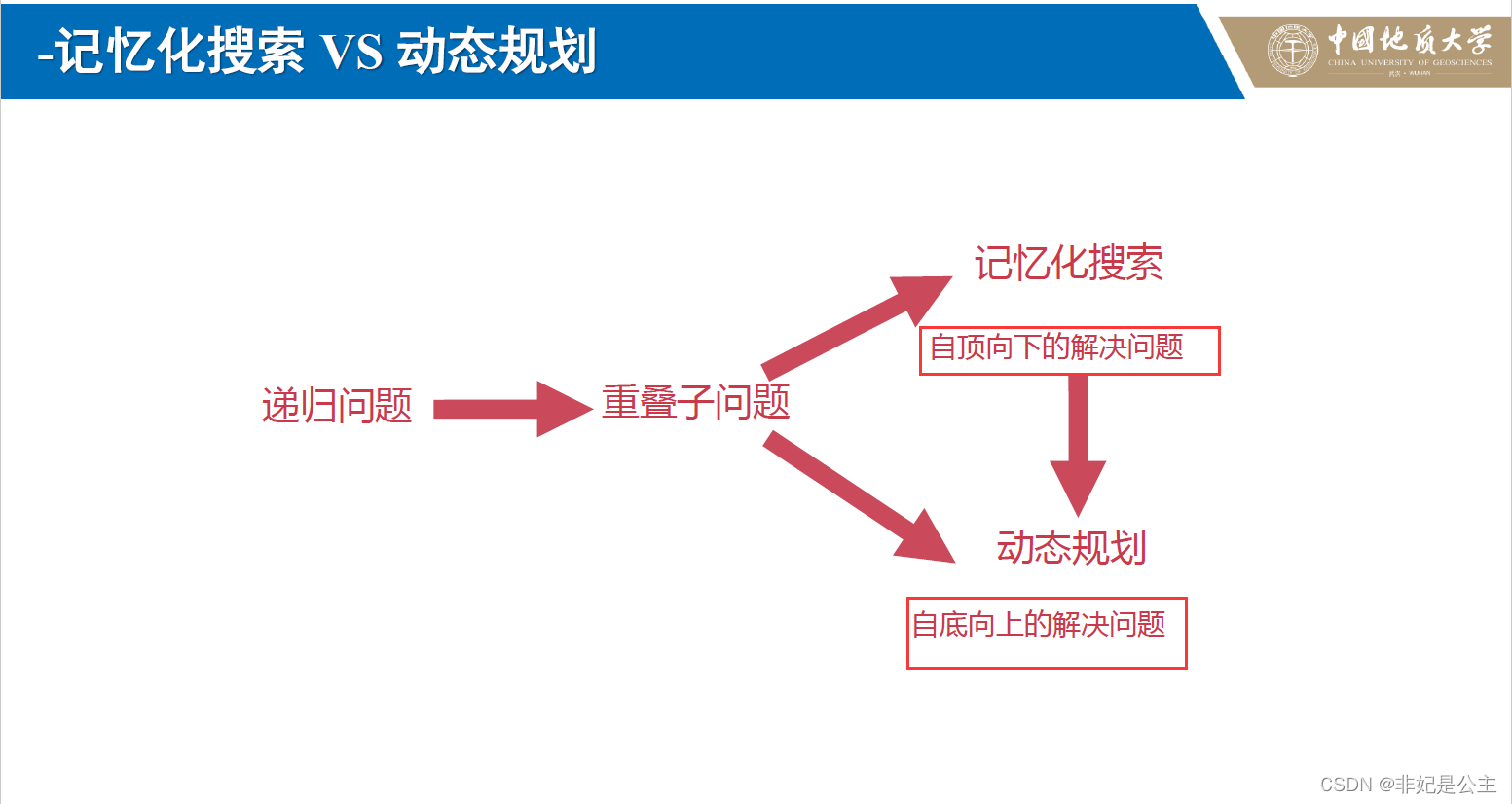
不同之处在于，动态规划自底向上进行计算，记忆化搜索自顶向下计算
在这里插入图片描述

矩阵链乘法+凸多边形剖分

矩阵链乘法

纯递归方法，根据动态转移方程：
在这里插入图片描述
其中，RecurMatrixChain(i, k, s, p)为矩阵i到矩阵k所需要的最少数乘次数。

int RecurMatrixChain(int i, int j, int** s, int* p)
{
	if (i == j) return 0;
	int u = INT_MAX;
	for (int k = i; k < j; k++)
	{
		int t = RecurMatrixChain(i, k, s, p)
			+ RecurMatrixChain(k + 1, j, s, p) + p[i - 1] * p[k] * p[j];
		if (t < u)
		{
			u = t;
			s[i][j] = k;
		}
	}
	return u;
}

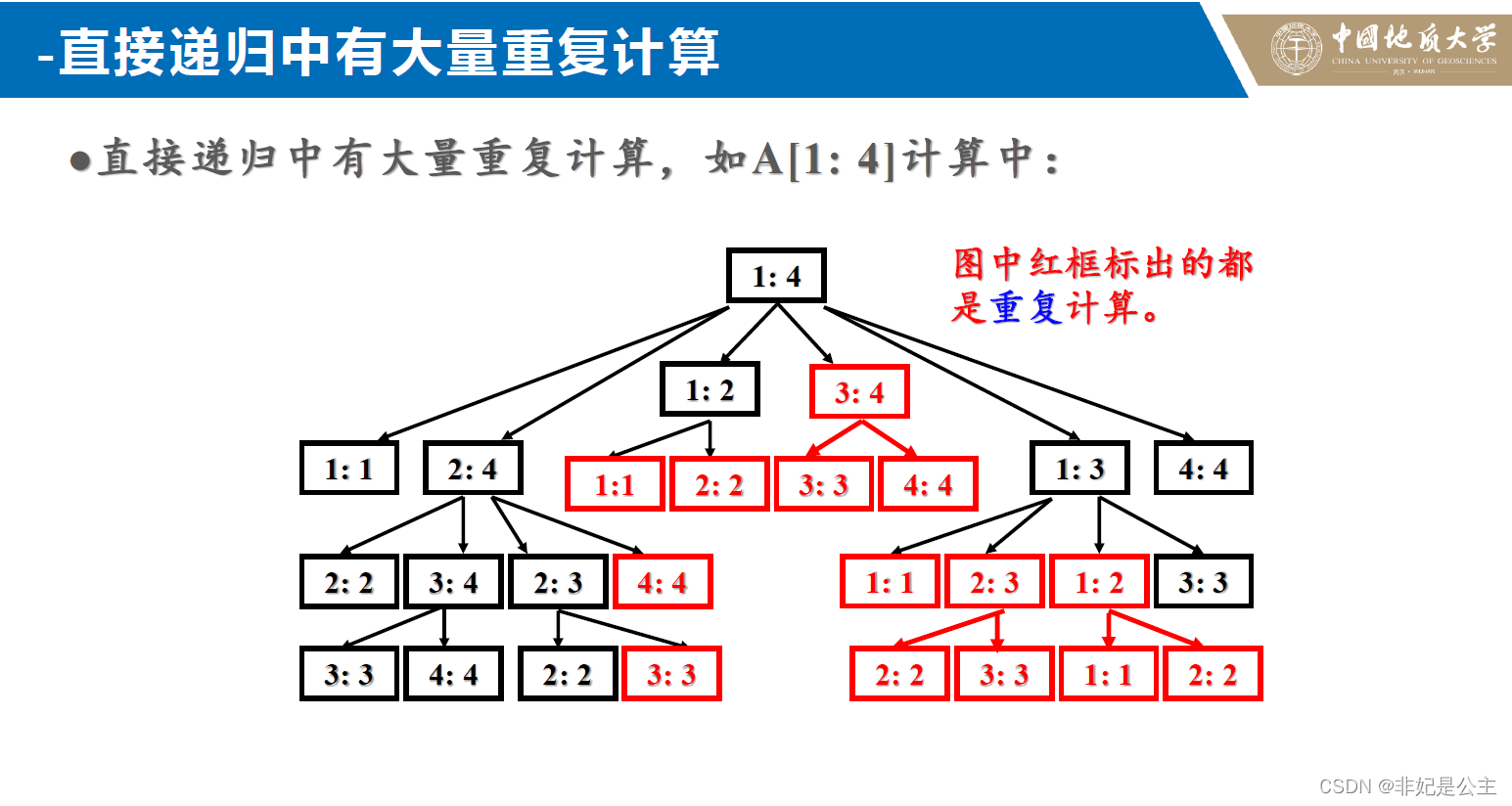
在这里插入图片描述
消除重复计算的方法：
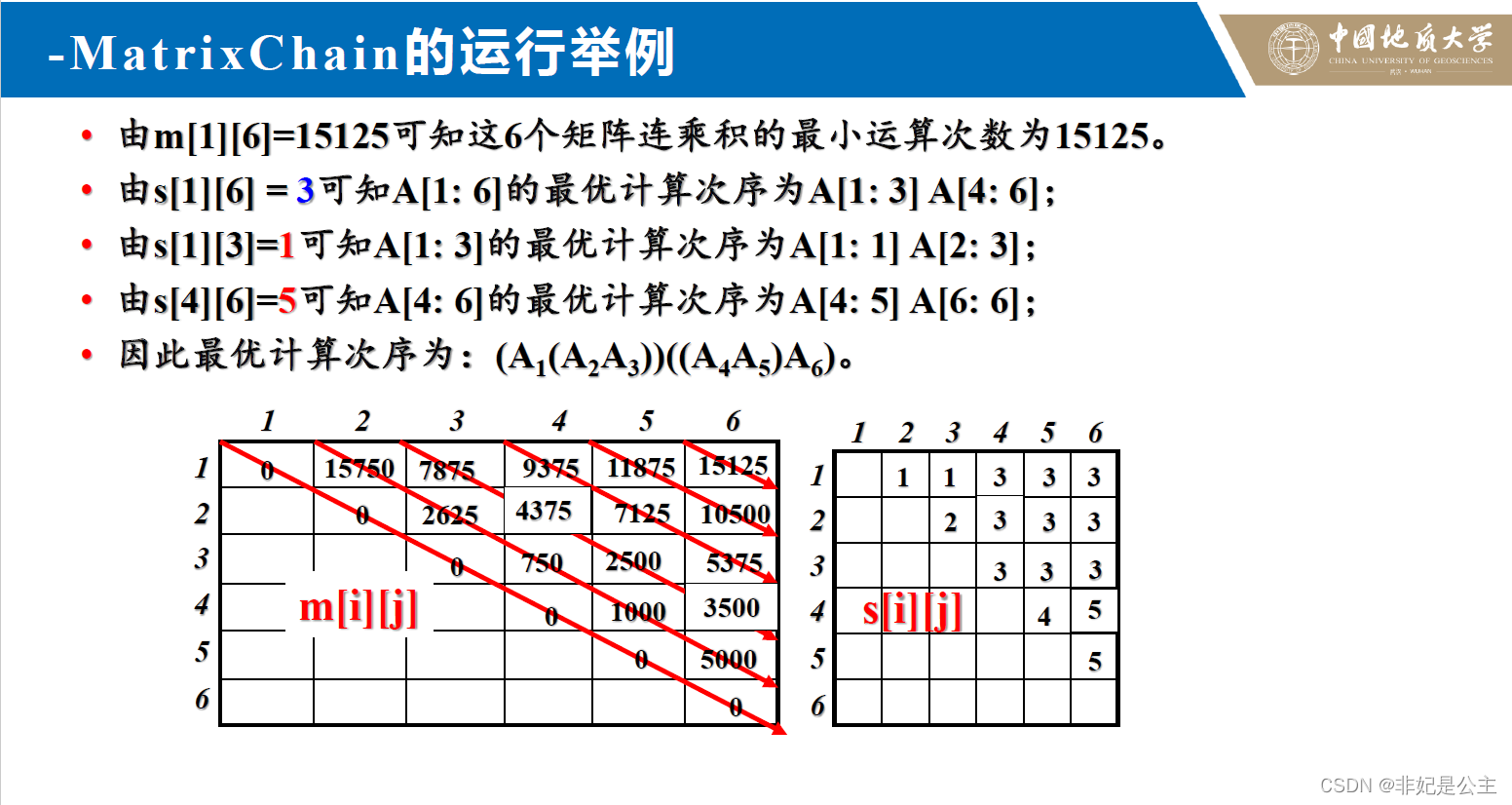
在这里插入图片描述
通过一个 O ( n 2 ) O(n^2) O(n2)的表格进行记录，沿对角线进行计算。
时间复杂度：
O ( n 3 ) O(n^3) O(n3)
空间复杂度：
O ( n 2 ) O(n^2) O(n2)
核心代码如下：

void MatrixChain(vector<int>& p, int n, vector<vector<int>>& m, vector<vector<int>>& s)
{
	for (int a = 1; a <= n; a++)
		m[a][a] = 0;
	for (int r = 2; r <= n; r++)
		for (int i = 1; i <= n - r + 1; i++)
		{
			int j = i + r - 1;
			m[i][j] = INT_MAX;
			for (int k = i; k < j; k++)
			{
				int t = m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j];
				if (t < m[i][j])
				{
					m[i][j] = t; s[i][j] = k;
				}
			}
		}
}

解追溯与测试代码如下：

int Traceback(int i, int j, vector<vector<int>> s) //找出s数组中记录的最优断开点
{
	if (i == j)
		return -1;
	Traceback(i, s[i][j], s);
	Traceback(s[i][j] + 1, j, s);
	cout << "包含矩阵A" << s[i][j];
	cout << "的部分与包含矩阵A" << (s[i][j] + 1)
		<< "的部分结合，放在一个括号中" << endl;
	return 0;
}

int main() {
	int n = 6;
	vector<vector<int>> m(n + 1, vector<int>(n + 1));
	vector<vector<int>> s(n + 1, vector<int>(n + 1));

	vector<int> p(n + 1);
	p = { 5,10,3,12,5,50,6 };

	MatrixChain(p, n, m, s);
	for (int i = 0; i < n+1; i++) {
		for (int j = 0; j < n+1; j++) {
			cout << "\t" << m[i][j] << "\t";
		}
		cout << endl;
	}
	cout << endl;
	for (int i = 0; i < n + 1; i++) {
		for (int j = 0; j < n + 1; j++) {
			cout << "\t" << s[i][j] << "\t";
		}
		cout << endl;
	}
	Traceback(1, n, s);
}

凸多边形剖分

在这里插入图片描述
参考leetcode上题leetcode1039：多边形三角剖分的最低得分
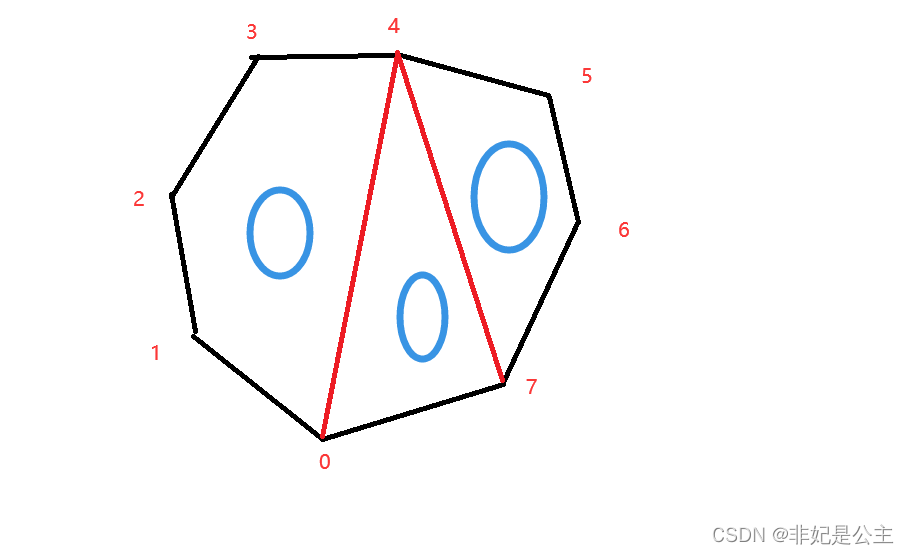
在这里插入图片描述
其中，按照leetcode1039题目给出的权函数定义，所得最优子结构性质如下：
t [ i ] [ j ] = { 0 j - i <= 1 t [ i ] [ k ] + t [ k ] [ j ] + v a l u e s [ i ] × v a l u e s [ k ] × v a l u e s [ j ]  j- i > 1 t[i][j]=\left\{ \begin{matrix} 0& \text{j - i <= 1} \\ t[i][k]+t[k][j]+values[i]\times{values[k]}\times{values[j]}& \text{ j- i > 1} \end{matrix} \right. t[i][j]={0t[i][k]+t[k][j]+values[i]×values[k]×values[j]​j - i <= 1 j- i > 1​
leetcode1039题解如下：

class Solution {
public:
    int minScoreTriangulation(vector<int>& values) {
        int n = values.size();
        vector<vector<int>> dp(n, vector<int>(n));
        /*for (int i = 0; i < n; i++) {
            dp[i][i + 1] = 0;
        }*/
        for (int r = 3; r <= n; r++) //r为当前计算的链长（子问题规模）
        {
            for (int i = 0; i <= n - r; i++) //n-r+1为最后一个r链的前边界
            {
                int j = i + r - 1;  //计算前边界为i，链长为r的链的后边界
                dp[i][j] = INT_MAX; //将链ij划分为A(i) * ( A[i+1:j] )这里实际上就是k=i
                //s[i][j] = i;
                for (int k = i + 1; k < j; k++) {
                    //将链ij划分为( A[i:k] )* (A[k+1:j])
                    int u = dp[i][k] + dp[k][j] + 
                        values[i] * values[k] * values[j];
                    if (u < dp[i][j]) {
                        dp[i][j] = u;
                        //s[i][j] = k;
                    }
                }
            }
        }
        return dp[0][n-1];
    }
};
// 测试用例
int main() {
    Solution solution;
    vector<int>values = { 3,7,4,5 };
    int n = solution.minScoreTriangulation(values);
    cout << n;
}

最长公共子序列

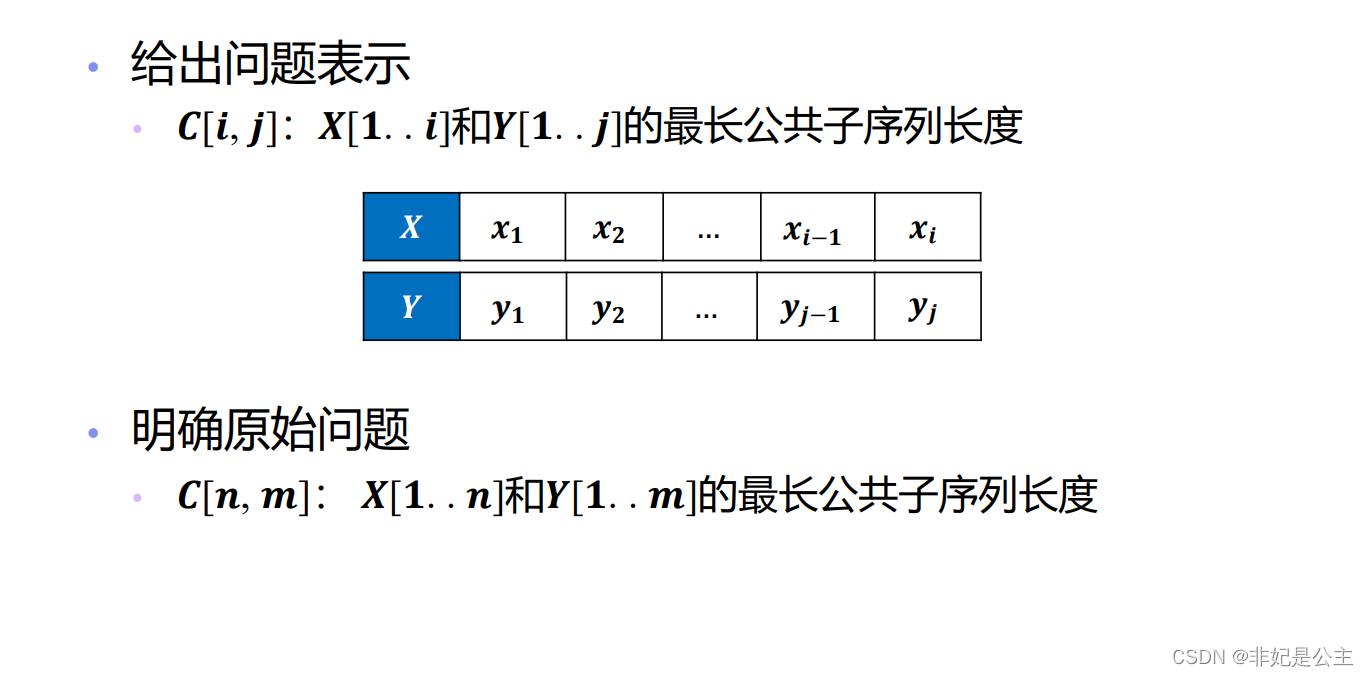
在这里插入图片描述
在这里插入图片描述
最优子结构性质：
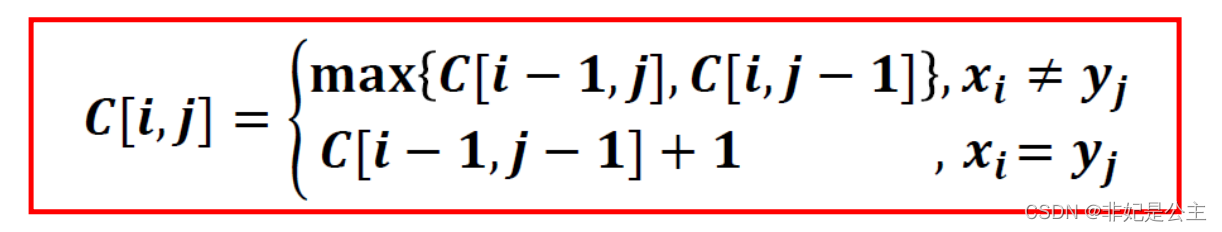
在这里插入图片描述
填表过程：
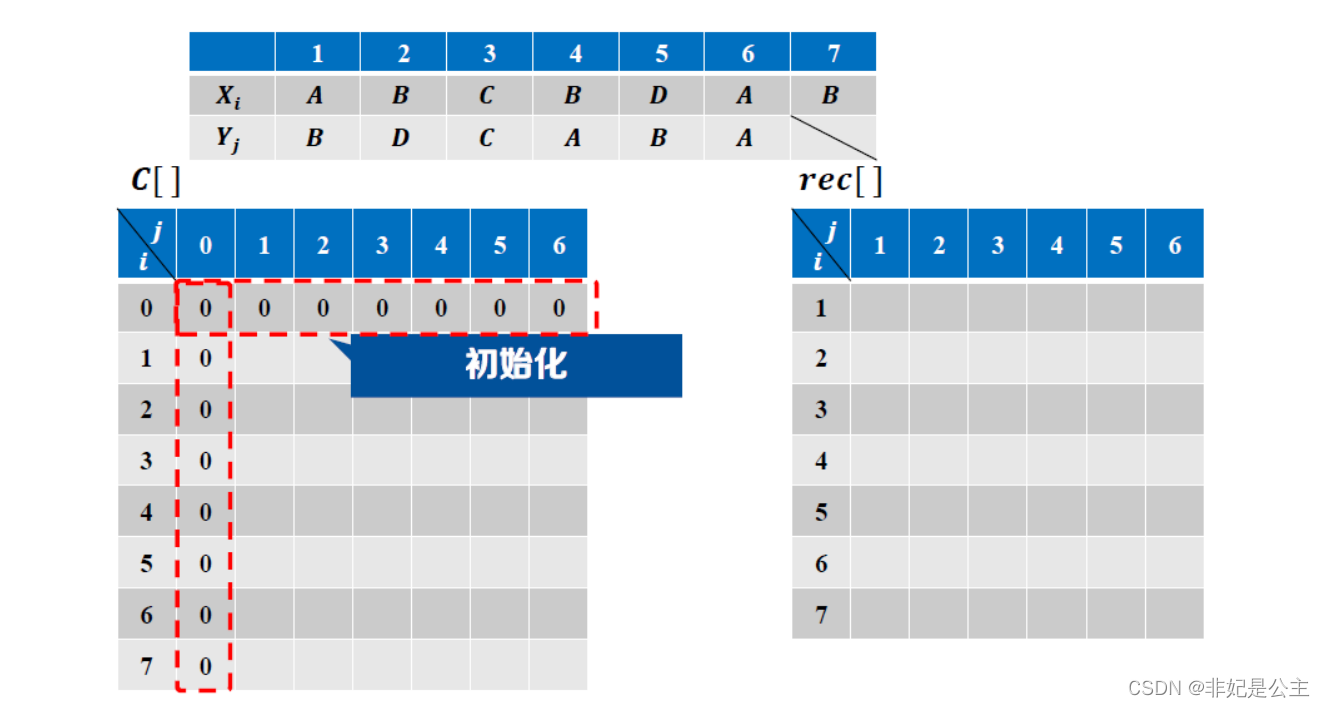
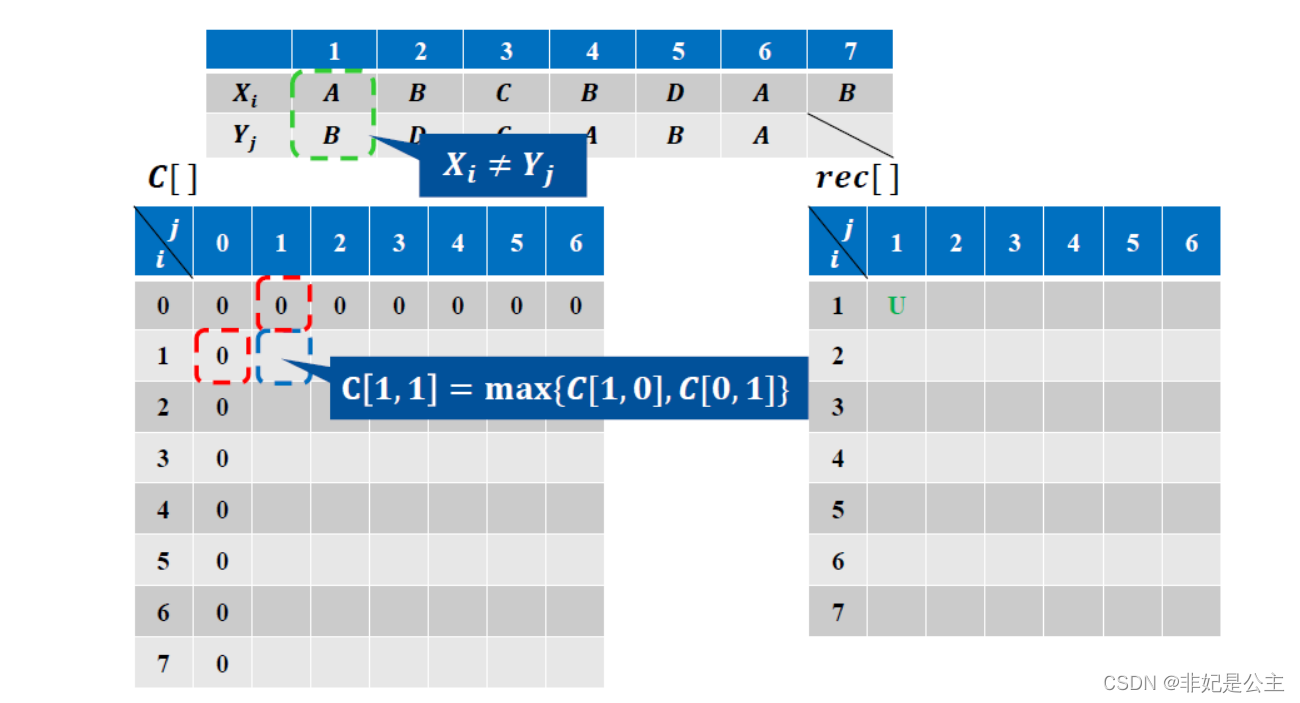
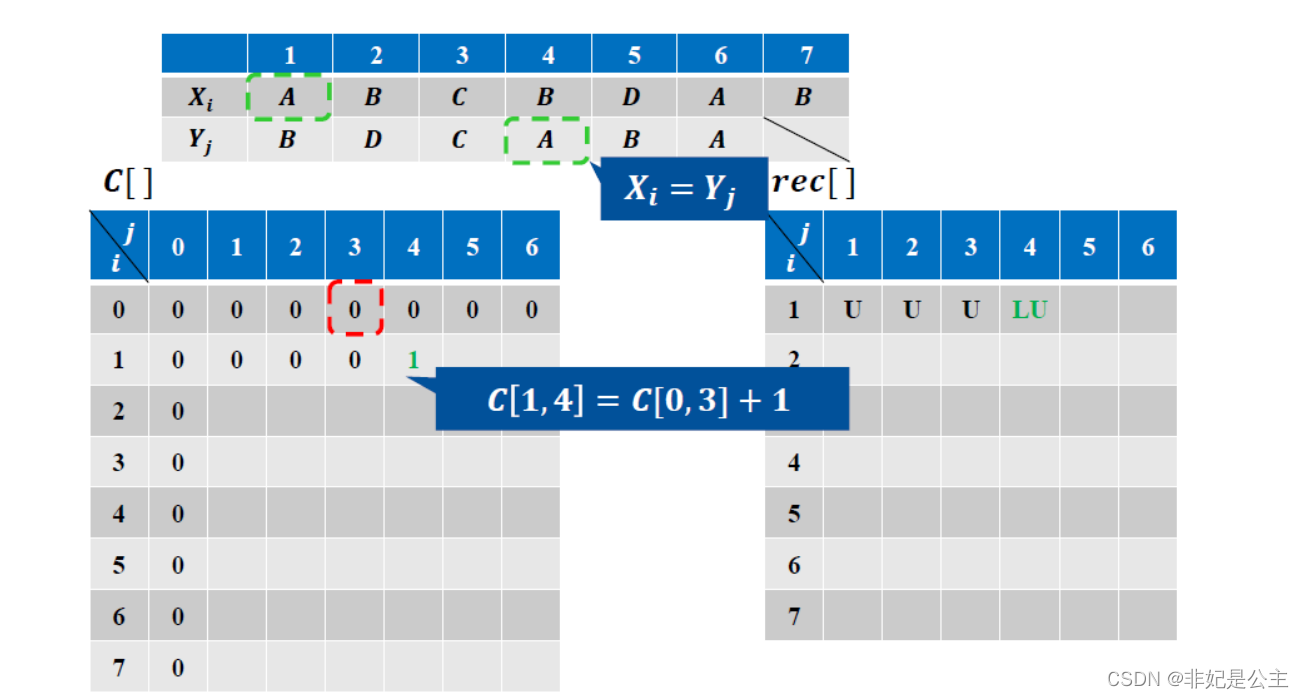
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述
核心代码：

#include<string>
#include<vector>
#include<iostream>
using namespace std;
class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        int m = text1.size();
        int n = text2.size();
        vector<vector<int>>C(m + 1, vector<int>(n + 1));
        vector<vector<int>>rec(m + 1, vector<int>(n + 1));
        for (int i = 1; i < m + 1; i++) {
            for (int j = 1; j < n + 1; j++) {
                if (text1[i - 1] == text2[j - 1]) {
                    C[i][j] = C[i - 1][j - 1] + 1;
                    rec[i][j] = 1;
                }
                else if (C[i][j - 1] > C[i - 1][j]) {
                    C[i][j] = C[i][j - 1];
                    rec[i][j] = 2;
                }
                else {
                    C[i][j] = C[i - 1][j];
                    rec[i][j] = 3;
                }
            }
        }
        int i = m;
        int j = n;
        while (i > 0 && j > 0) {
            if (rec[i][j] == 1) { 
                cout << text1[i - 1]; 
                i--;
                j--;
            }
            else if (rec[i][j] == 2) {
                j--;
            }
            else {
                i--;
            }
        }
        return C[m][n];
    }
};

int main() {
    string text1 = "ybl";
    string text2 = "yby";
    Solution solution;
    int num = solution.longestCommonSubsequence(text1, text2);
    cout << endl << num;
}

最大子段和（字数组）

在这里插入图片描述
状态转移方程：
m a x v a l u e [ i ] = { m a x v a l u e [ i − 1 ] + n u m [ i ]  maxvalue[i-1] + num[i] > maxvalue[i-1]  m a x v a l u e [ i − 1 ]  maxvalue[i-1] + num[i] < maxvalue[i-1]  maxvalue[i]=\left\{ \begin{matrix} maxvalue[i-1] + num[i]& \text{ maxvalue[i-1] + num[i] > maxvalue[i-1] } \\ maxvalue[i-1] & \text{ maxvalue[i-1] + num[i] < maxvalue[i-1] } \end{matrix} \right. maxvalue[i]={maxvalue[i−1]+num[i]maxvalue[i−1]​ maxvalue[i-1] + num[i] > maxvalue[i-1]  maxvalue[i-1] + num[i] < maxvalue[i-1] ​

//方法1：
class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int pre = 0;
        int maxvalue = INT_MIN;
        for (auto num : nums) {
            pre = max(pre + num, num);
            maxvalue = max(maxvalue, pre);
        }
        return maxvalue;
    }
};

0-1背包

问题描述：
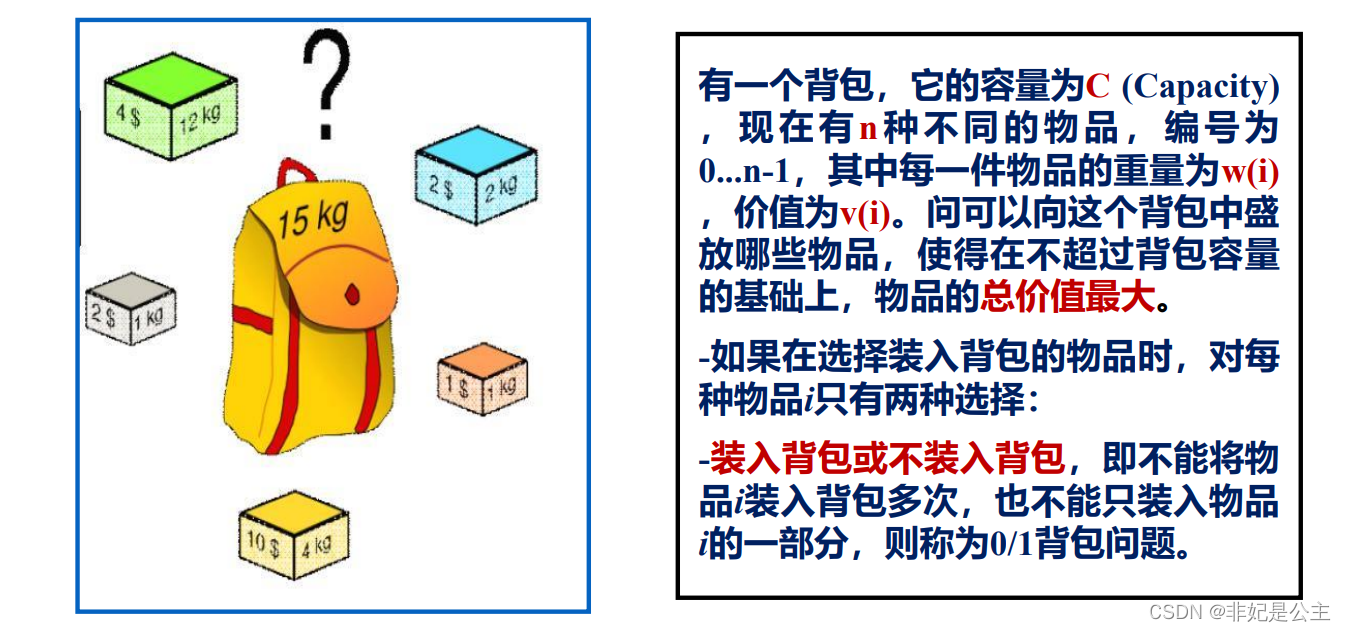
在这里插入图片描述
状态转移方程：
K n a p s a c k S R ( h , i , C ) = m a x ( K n a p s a c k S R ( h , i − 1 , C ) ， K n a p s a c k S R ( h , i − 1 , C − V [ i ] ) + P [ i ] ) KnapsackSR(h,i,C)=max(KnapsackSR(h,i-1,C)，KnapsackSR(h,i-1,C-V[i])+P[i]) KnapsackSR(h,i,C)=max(KnapsackSR(h,i−1,C)，KnapsackSR(h,i−1,C−V[i])+P[i])
递归求解：
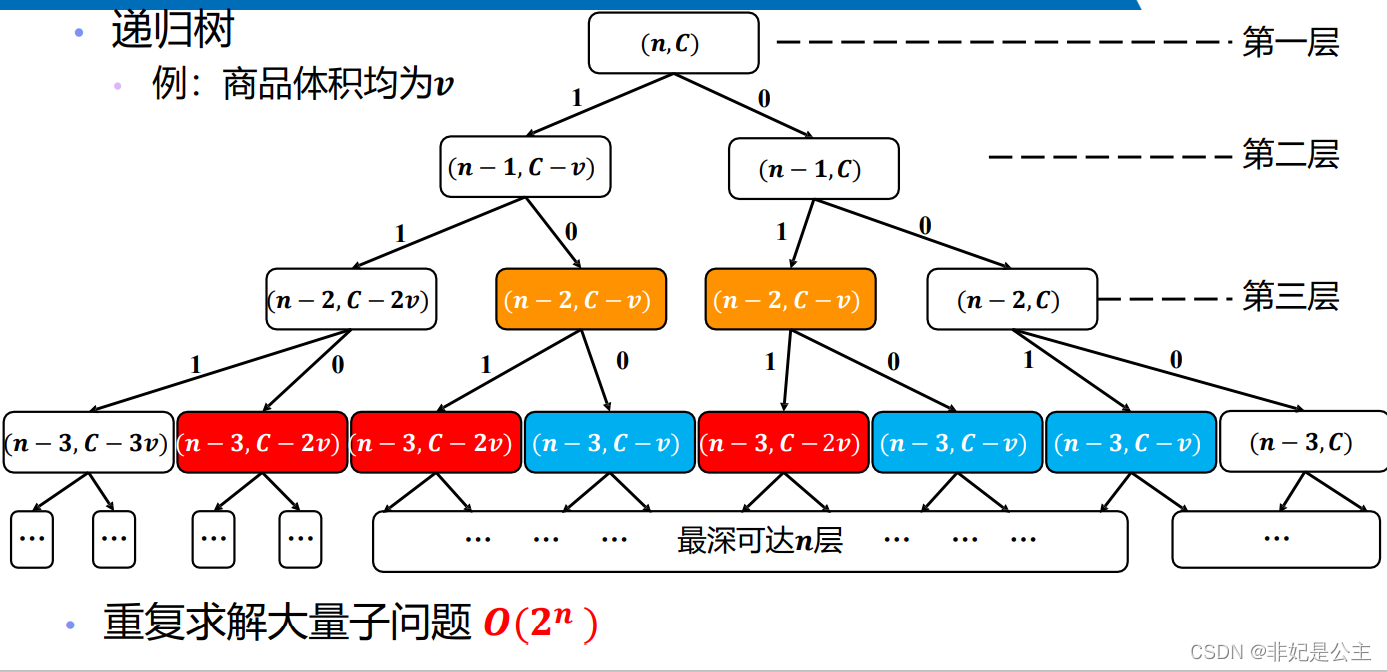
在这里插入图片描述
在这里插入图片描述
dp求解（填表）：
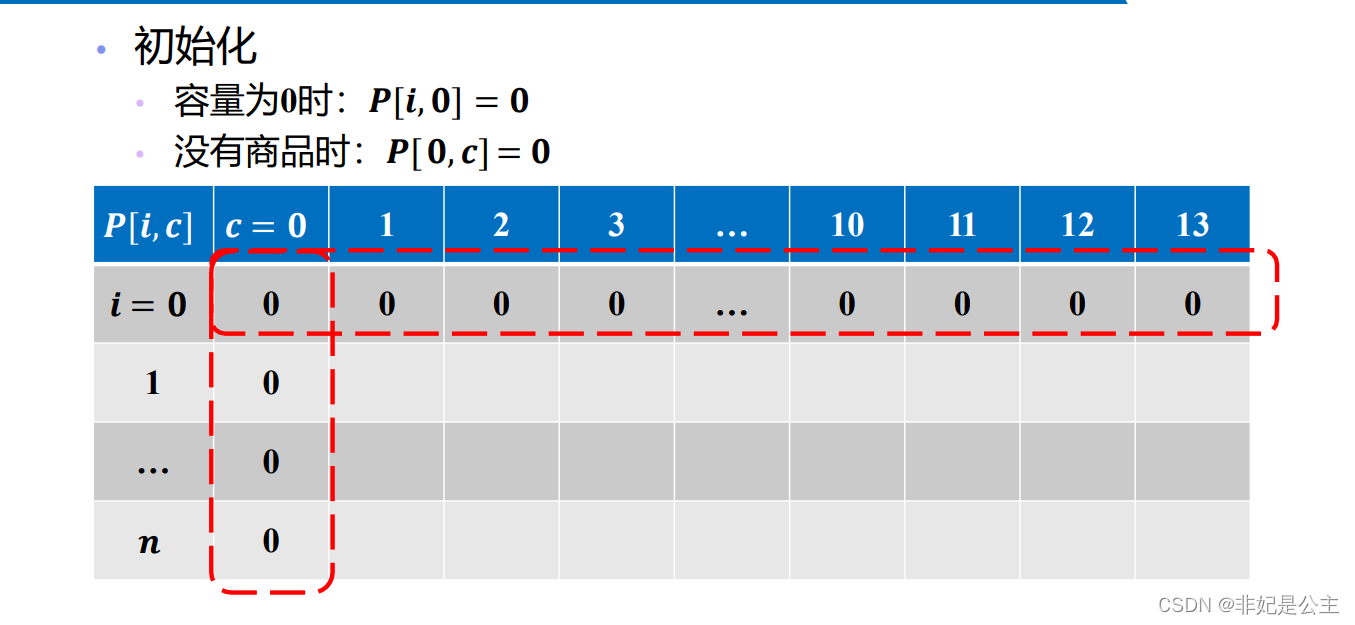
在这里插入图片描述
在这里插入图片描述
leetcode416：分割和子集（和0-1背包问题）核心代码：

#include<vector>
#include<iostream>
using namespace std;
class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int sum = 0;
        for (auto num : nums) {
            sum += num;
        }
        if (sum % 2)return false;
        int C = sum / 2;
        vector<vector<int>> dp(nums.size(), vector<int>(C + 1));
        for (int i = 0; i < nums.size(); i++) {
            for (int j = 1; j < dp[0].size(); j++) {
                if (i == 0) {
                    dp[i][j] = nums[i] > j ? 0 : nums[i];
                }
                else if (j < nums[i])
                    dp[i][j] = dp[i - 1][j];
                else
                    dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - nums[i]] + nums[i]);
            }
            if (dp[i][dp[0].size() - 1] == C)return true;
        }
        return false;
    }
};

int main() {
    vector<int> nums = { 1,2,5 };
    Solution solution;
    cout << solution.canPartition(nums);
}

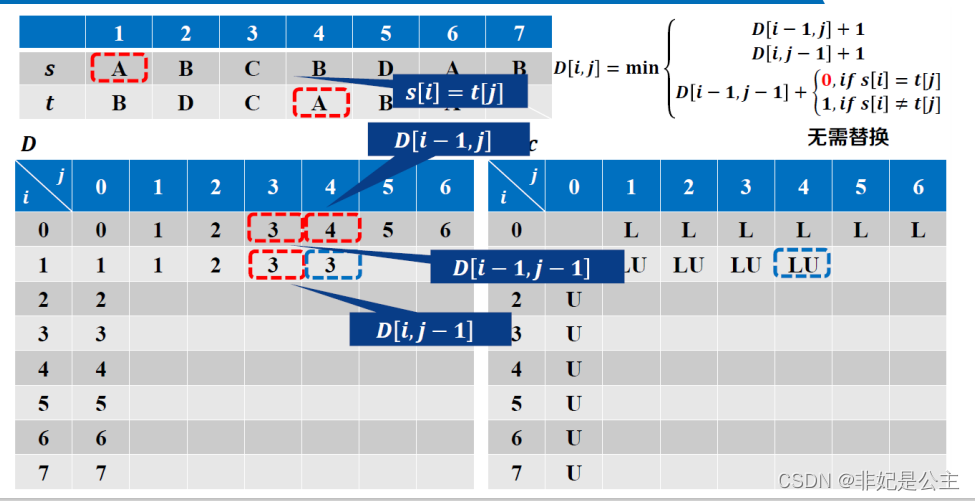
编辑距离

问题描述：
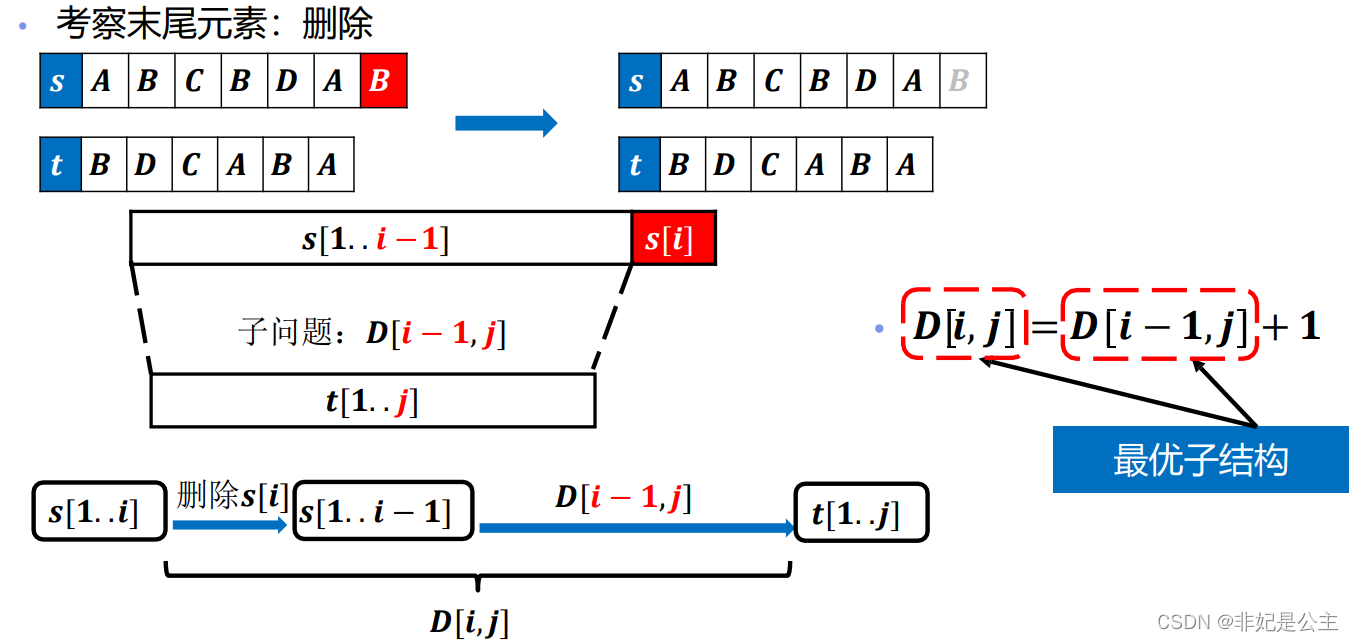
在这里插入图片描述
删除：
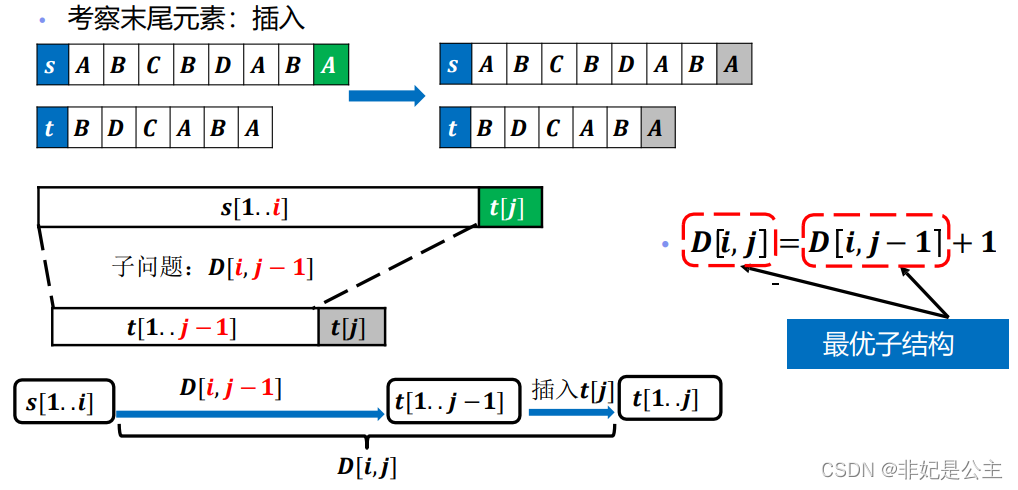
在这里插入图片描述
插入：
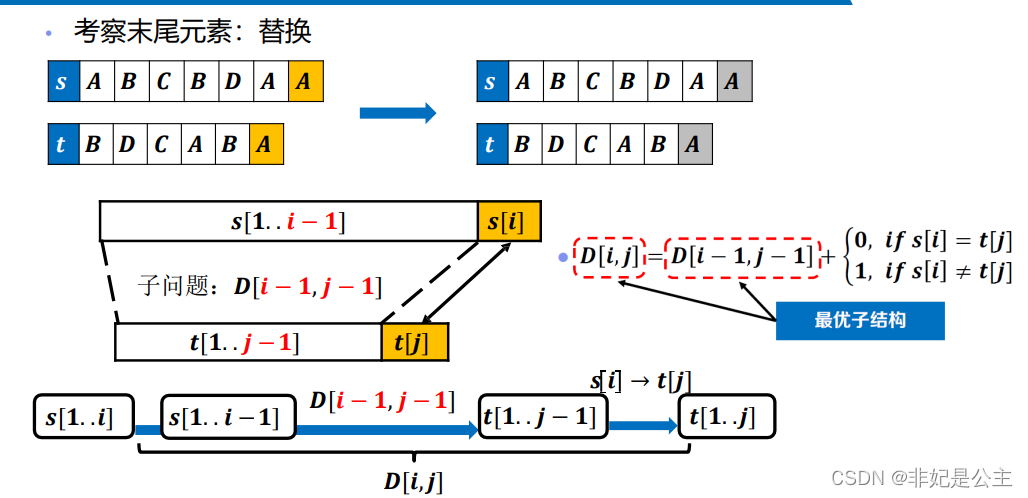
在这里插入图片描述
替换：
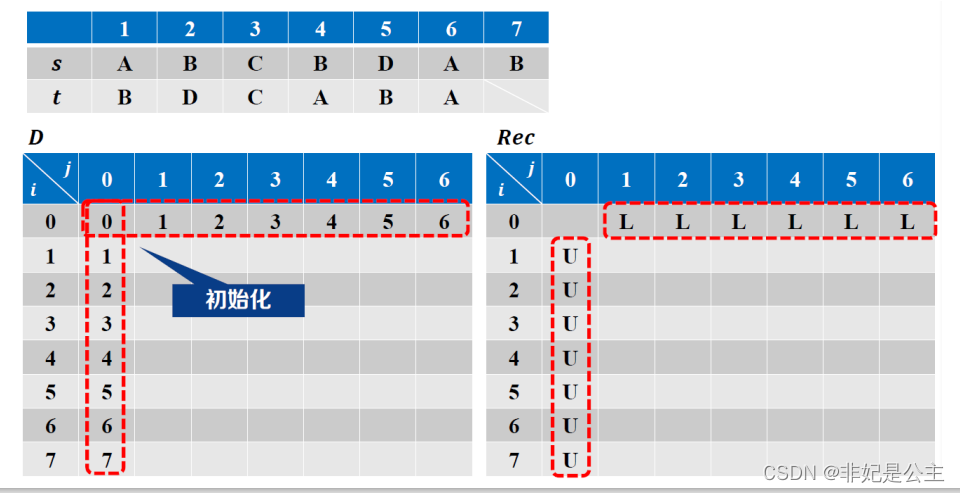
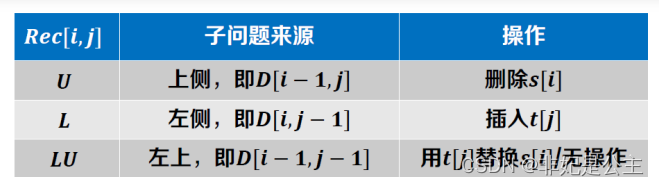
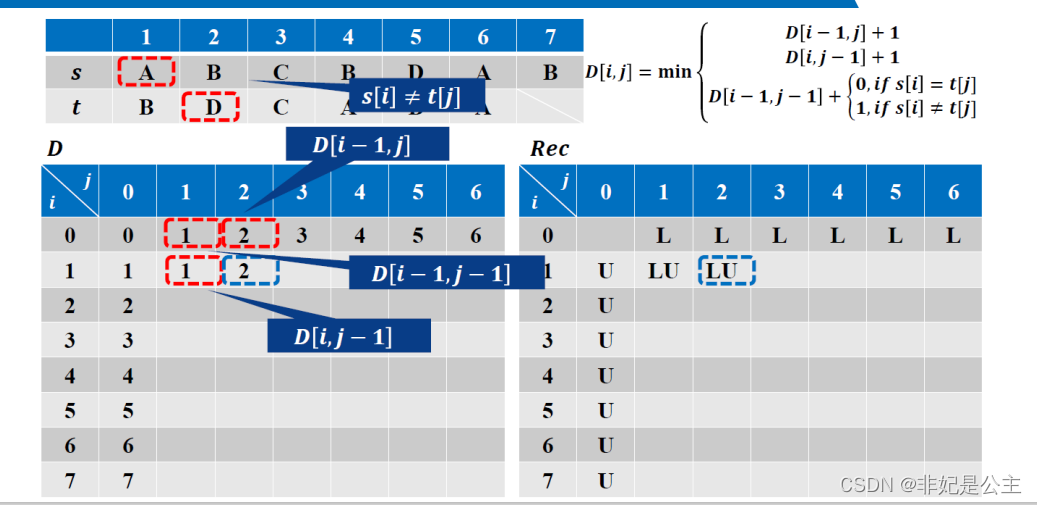
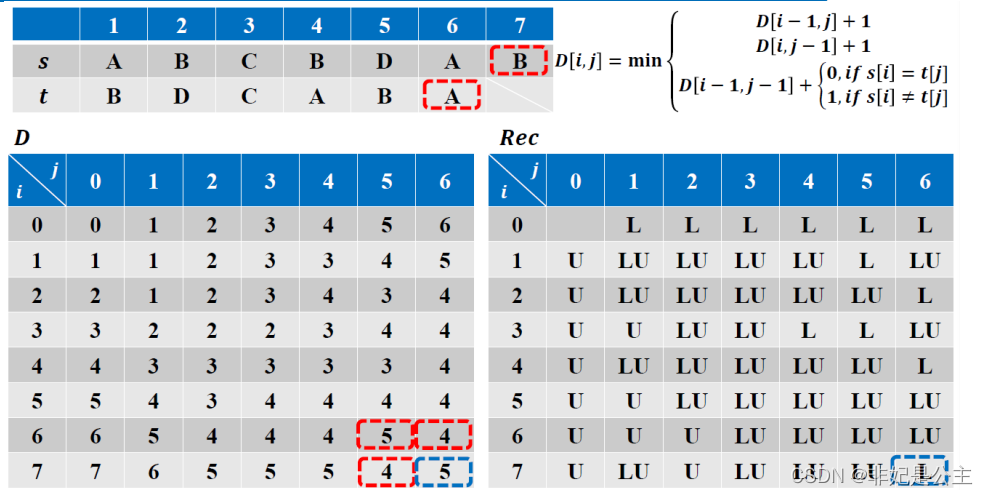
在这里插入图片描述
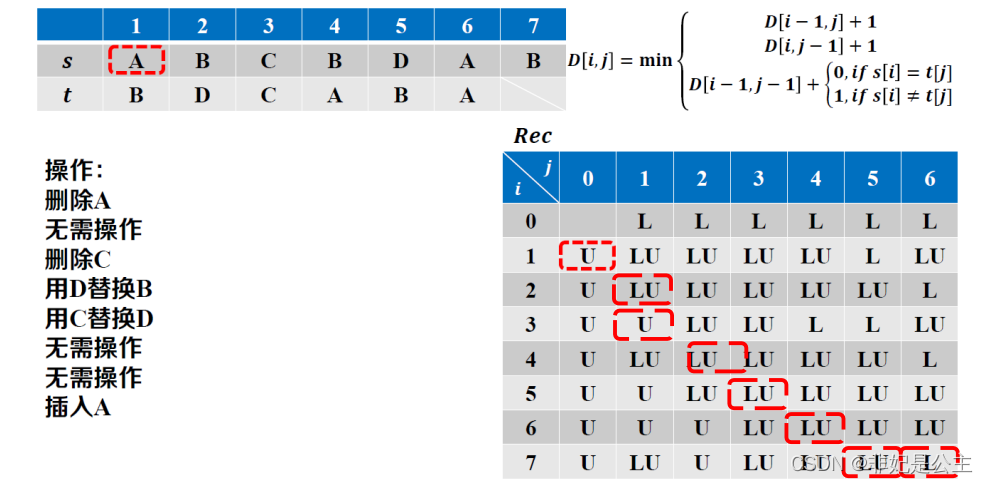
在这里插入图片描述
填表：
在这里插入图片描述
在这里插入图片描述在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
追溯解：
在这里插入图片描述
leetcode72：编辑距离核心代码：

#include<string>
#include<vector>
#include<iostream>
using namespace std;
class Solution {
public:
    int minDistance(string word1, string word2) {
        int m = word1.size() + 1;
        int n = word2.size() + 1;
        vector<vector<int>> dp(m, vector<int>(n));
        for (int i = 0; i < m; i++) {
            dp[i][0] = i;
        }
        for (int j = 0; j < n; j++) {
            dp[0][j] = j;
        }
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (word1[i - 1] == word2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1];
                }
                else {
                    dp[i][j] = min(min(dp[i - 1][j] + 1, dp[i][j - 1] + 1),
                        dp[i - 1][j - 1] + 1);
                }
            }
        }
        return dp[m - 1][n - 1];
    }
};

int main() {
    string s1 = "horse";
    string s2 = "ros";
    Solution solution;
    int res = solution.minDistance(s1, s2);
    cout << res;
    return 0;
}

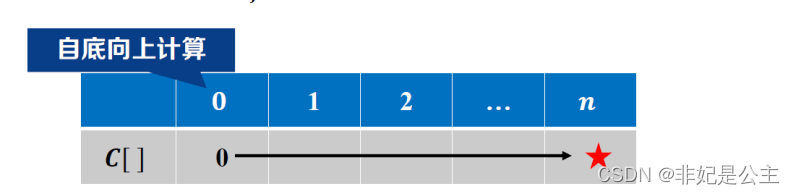
钢条切割

状态转移方程：
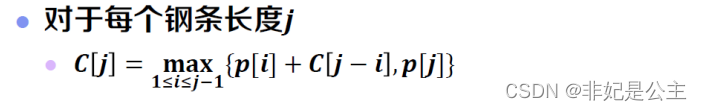
在这里插入图片描述
在这里插入图片描述

#include<vector>
#include<iostream>
using namespace std;

int CutFe(vector<int>p, int n) {
	vector<int>C(n + 1);
	for (int i = 0; i < n + 1; i++) {
		int t = i - p.size() + 1;
		for (int j = max(t, 0); j < i; j++) {//i-p.size()+1
			C[i] = max(C[i], C[j] + p[i - j]);
		}
	}
	return C[n];
}
int main() {
	vector<int> p = { 0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 24 };	
	cout << CutFe(p, 10);
	return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/131937.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

pycharm-qt5-designer1

pycharm-qt5-designer1

pycharm-qt5-designer1一: designer界面介绍1. 新建模板二: 控件箱简介1. Layouts 布局2. Spacers 间隔(透明)3. Button4. Item views5. Item Widgets 条目控件6. Containers 容器7. input Widgets 输入控件8. Display Widgets 显示控件三: 控件属性简介1. sizePolicy: 控件大小…
阅读更多...
gitlab-ci.yml关键字（四）allow_failure 、artifacts 、cache

gitlab-ci.yml关键字（四）allow_failure 、artifacts 、cache

allow_failure 我们知道&#xff0c;流水线作业在运行时如果失败了&#xff0c;就会停止运行&#xff0c;但allow_failure可以让我们自由的控制当前作业失败时&#xff0c;是否还需要继续运行。 要让管道继续运行后续作业&#xff0c;请使用allow_failure: true要停止管道运行…
阅读更多...
OASIS协议标准文档的解读_第一部分

OASIS协议标准文档的解读_第一部分

译者注&#xff1a; 利用2022年圣诞假期&#xff0c;终于解读完OASIS标准协议的文档。本翻译文档基于SEMI 草案标准 3626 (2003/04/23). 因为SEMI的原版标准草案涉及到版权的一些问题&#xff0c;并不是公开的。因此我并不是原文原样翻译&#xff0c;会加入很多我自己的理解和…
阅读更多...
cnpm : 无法将“cnpm”项识别为 cmdlet、函数、脚本文件或可运行程序的名称。请检查名称的拼写，如果包括路径，请确保路径正确，然后再试一次。

cnpm : 无法将“cnpm”项识别为 cmdlet、函数、脚本文件或可运行程序的名称。请检查名称的拼写，如果包括路径，请确保路径正确，然后再试一次。

从报错来看明显是没有装 cnpm 检查本地是否安装了cnpm包管理工具 命令&#xff1a;npm list --depth0 -global 查看一下电脑是否安装了cnpm 如果已经安装了&#xff0c;那么会有如下图所示的内容&#xff1a; 从以上来看确实是没有装 则需要安装镜像&#xff0c;执行命令为…
阅读更多...
Vue3详细讲解

Vue3详细讲解

Vue 3 介绍 文章目录Vue 3 介绍为什么要学习 vue 3Vue3 动机 和 新特性Vite 的使用vite介绍为什么选 Vite &#xff1f;Vite 的基本使用Vue3.0项目介绍vscode插件说明组合式APIcomposition API vs options API体验 composition APIsetup 函数reactive 函数ref 函数script setup…
阅读更多...
【云原生 | Kubernetes 实战】19、K8s Ingress-Controller 高可用方案

【云原生 | Kubernetes 实战】19、K8s Ingress-Controller 高可用方案

目录 一、Ingress 和 Ingress Controller 概述 1.1 回顾下 service 四层代理 1.2 Ingress 介绍 1.3 Ingress Controller 介绍 1.4 Ingress 和 Ingress Controller 总结 1.5 使用 Ingress Controller 代理 k8s 内部 pod 的流程 二、创建两个 ingress-controller 高可用…
阅读更多...
凌云驭势 亚马逊云科技开启re:Invent中国行

凌云驭势 亚马逊云科技开启re:Invent中国行

‍‍数据智能产业创新服务媒体——聚焦数智 改变商业近日&#xff0c;亚马逊云科技召开了2022 re:Invent全球大会。作为云计算的开创者&#xff0c;每年亚马逊云科技举办的re:Invent全球大会都会成为产业的风向标&#xff0c;备受业内人士关注。2022年&#xff0c;面对全球数字…
阅读更多...
【STL学习之路】vector的模拟实现

【STL学习之路】vector的模拟实现

文章目录一、接口总览二、vector成员变量三、默认成员函数构造函数① -- 默认无参构造构造函数② -- 迭代器区间构造构造函数③ -- n个val构造拷贝构造函数赋值运算符重载析构函数四、迭代器六、容量以及元素访问的相关接口emptysize和capacityreserveresize七、增删查改等接口…
阅读更多...
async await 的基础使用和实现原理

async await 的基础使用和实现原理

async await 使用基础原理 async/await用法 其实你要实现一个东西之前&#xff0c;最好是先搞清楚这两样东西 这个东西有什么用&#xff1f; 这个东西是怎么用的&#xff1f; 有什么用&#xff1f; async/await的用处就是&#xff1a;用同步方式&#xff0c;执行异步操作&…
阅读更多...
商会机构源码模板系统包含了信息管理、新闻管理、广告管理、系统管理等功能 v3.9

商会机构源码模板系统包含了信息管理、新闻管理、广告管理、系统管理等功能 v3.9

内容目录一、详细介绍二、效果展示1.部分代码2.效果图展示三、学习资料下载一、详细介绍 XYCMS商会机构源码模板系统是以aspaccess进行开发的商会网站源码&#xff0c;包含了信息管理、新闻管理、广告管理、系统管理等功能。 XYCMS商会机构源码模板系统功能简述&#xff1a; 商…
阅读更多...
大数据面试题Spark篇（1）

大数据面试题Spark篇（1）

1.spark数据倾斜 数据倾斜俩大直接致命后果&#xff1a;Out Of Memory&#xff0c;运行速度慢。这主要是发生在Shuffle阶段。同样Key的数据条数太多了。导致了某个key所在的Task数据量太大了&#xff0c;远远超过其他Task所处理的数据量。 数据倾斜一般会发生在shuffle过程中…
阅读更多...
使用Eclipse开发第一个Java程序

使用Eclipse开发第一个Java程序

虽然在《使用记事本编写运行Java程序》一节中已经开发过一个 Java 程序&#xff0c;但是那毕竟是通过记事本创建的。在上一节《Java Eclipse下载安装教程》中&#xff0c;我们已经安装了 Eclipse 工具&#xff0c;因此本节将介绍如何通过 Eclipse 开发 Java 程序。 在 Eclipse …
阅读更多...
SD存储卡介绍

SD存储卡介绍

SD存储卡简介 SD存储卡是一种基于半导体快闪记忆器的新一代记忆设备&#xff0c;由于它体积小、数据传输速度快、可热插拔等优良的特性&#xff0c;被广泛地于便携式装置上使用&#xff0c;例如数码相机、平板电脑、多媒体播放器等。 SD存储卡实物图 SD存储卡特点 1、高存储容…
阅读更多...
痞子衡嵌入式：Farewell, 我的写博故事2022

痞子衡嵌入式：Farewell, 我的写博故事2022

-- 题图&#xff1a;苏州荷塘月色 2022 年的最后一天&#xff0c;写个年终总结。困扰大家三年之久的新冠疫情终于在 12 月全面放开了&#xff0c;痞子衡暂时还没有阳&#xff0c;计划坚持到总决赛。对于 2023 年&#xff0c;痞子衡还是充满期待的&#xff0c;慢慢要恢复到 2019…
阅读更多...
Codewars 你虐我千百遍，我待你如初恋

Codewars 你虐我千百遍，我待你如初恋

本人最近接触了Codewars啥的&#xff0c;没什么见识哈哈哈哈&#xff0c;刚开始看不懂啥的&#xff0c;到后面看多了其实也还好。我是小白轻点喷&#xff01;&#xff01;&#xff01;接下来就让我展示第一次写文章的历程吧&#xff0c;showTime&#xff1a; 第一位嘉宾A出场 …
阅读更多...
2022年终总结：生活就像一道过山车

2022年终总结：生活就像一道过山车

又到了年末&#xff0c;今年的年终总结我考虑了很久&#xff0c;到底要不要写&#xff1f;可以写些什么&#xff1f; 今年过得十分匆忙&#xff0c;我一直在赶路&#xff0c;但事实上今年内做完的&#xff0c;能说出口的事可以说没有。 回顾下去年对今年的期望&#xff1a; 有…
阅读更多...
魔幻2022，2023涅槃重生！

魔幻2022，2023涅槃重生！

前言&#xff1a; 大家好&#xff0c;按照惯例&#xff0c;每年的年尾&#xff0c;这个时候我都会进行复盘&#xff0c;这是自己第4个年头进行年度复盘&#xff1a;总结2019&#xff0c;展望2020&#xff01;不管过去如何&#xff0c;未来我们都要奋力前行&#xff01;复盘2021…
阅读更多...
01月份图形化三级打卡试题

01月份图形化三级打卡试题

活动时间 从2023年 1月1日至1月21日&#xff0c;每天一道编程题。 本次打卡的规则如下&#xff1a; &#xff08;1&#xff09;小朋友每天利用10~15分钟做一道编程题&#xff0c;遇到问题就来群内讨论&#xff0c;我来给大家答疑。 &#xff08;2&#xff09;小朋友做完题目后&…
阅读更多...
一个词语总结2022，你的是什么？ | 2022 年度总结

一个词语总结2022，你的是什么？ | 2022 年度总结

一个词语总结2022&#xff0c;你的是什么&#xff1f; | 2022 年度总结前言回顾2022蓄力Unity 可寻址系统Unity 发布微信小游戏Unity 发布抖音小游戏Unity Mac AppStore内购Unity 后期处理蓄势付费专栏联袂推荐签约作者年度回忆展望20232023flag前言 2022马上即将过去。近期各…
阅读更多...
机器学习理论和定理

机器学习理论和定理

在机器学习中&#xff0c; 有一些非常有名的理论或定理&#xff0c; 对理解机器学习的内在特性非常有帮助&#xff0e; 1. PAC学习理论 当使用机器学习方法来解决某个特定问题时&#xff0c; 通常靠经验或者多次试验来选择合适的模型、 训练样本数量以及学习算法收敛的速度等…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023