译者注: 利用2022年圣诞假期,终于解读完OASIS标准协议的文档。本翻译文档基于SEMI 草案标准 3626 (2003/04/23). 因为SEMI的原版标准草案涉及到版权的一些问题,并不是公开的。因此我并不是原文原样翻译,会加入很多我自己的理解和注释。 所以本文仅作兴趣研究,对其中的错误概不负责。希望能为支持国内半导体产业做点微薄贡献。
1. Purpose
1.1 本协议规范的目的是为了制定分层集成电路掩膜图形信息的交互和封装格式。
1.2 标准背景 – 略过。简单一句话就是克服GDSII协议标准的缺点,适应更大规模的集成电路设计制造。
2. Scope
2.1. 本规范制定的格式,最重要的目的就是用来封装分层集成电路掩膜图形 ,以便在各个EDA工具,掩膜制作,掩膜检查和修复工具之间交互。
2.2. 规范制定的格式,要求是硬件和软件之间相互独立,互不依赖。
3. Limitations
3.1 如果oasis文件使用了一些协议中规定的扩展记录(extension records), 比如XNAME, XELEMENT和XGEOMETRY, 可能会影响在不同工具之间的通用性。有些工具可能不支持这些扩展字段。因此推荐这些扩展字段只用在内部的原型设计中,如果需要对外交互,应该使用本规范正式包含的扩展字段。(备注:哪些是正式包含的扩展字段?)
4. Referenced Standards
4.1 IEEE Standards1
IEEE 754-1985 - IEEE Standard for Binary Floating-Point Arithmetic
4.2 ISO Standards2
ISO-646-IRV - “US-ASCII” Character Set ISO-3309 - Information technology—Telecommunications
and information exchange between systems—High-level data link control (HDLC) procedures—Frame structure
4.3 IETF Standards3
RFC 1951 - DEFLATE Compressed Data Format Specification version 1.3
5. Terminology
(译者:个人觉得术语这一部分还是不翻译的为好。所以这章大部分是原文copy过来了。)
5.1 简写词和首字母缩略词
5.1.1 BNF—Backus-Naur Form
5.1.2 EDA—Electronic Design Automation
5.1.3 1OASISTM—Open Artwork System Interchange Standard
5.2 术语定义
5.2.1 OASIS规范中大部分的术语定义都可以在上下文相关的段落中找到
5.2.2 Cell—a named object in a layout hierarchy, containing native geometric information, annotation information,
and/or placements of other cells. 一个基本的信息单元。可以是几何图形,也可以是注解信息,或者其它单元的位置放置信息,
5.2.3 Placement—a specification by reference that a copy of a cell is to be placed within the coordinate space of another cell at a particular location, orientation, and scale. Cell placement is the fundamental mechanism which makes hierarchy within the OASIS file possible. 信息单元的位置放置信息。包括了坐标,方向,缩放等信息。
5.2.4 Geometry—a two-dimensional geometric figure such as a polygon, rectangle, trapezoid, path, circle, etc. with inherent attributes of layer and datatype. 几何信息,包括多边形,长方形,正方形,路径,圆等图形的几何坐标信息。
5.2.5 Property—an annotation element consisting of a name plus an optional list of values, supplying descriptive information about the characteristics of the file or one of its components. 属性信息。比如名字,注释,描述等信息。
5.2.6 Record—the principal data division in an OASIS file. 记录块,OASIS文件中的一个基本的数据块。
5.2.7 Text Element—an annotation element consisting of an (x,y) coordinate point and an associated string. 文本信息。包括注释信息以及放置的坐标位置。
5.3 Symbols
5.3.1 “->” — 用来标明一个参数名称和它的内容。
6. OASIS BASICS
6.1 OASIS文件时流格式的文件格式。分成一个个数据块(record). 每个数据块的长度是可以通过解析它的结构来获取的,但这个长度不是明确的。就是需要解析它才能获取这个数据块的长度。(相反的gds2的文件格式,每个数据块的长度是明确的。)
6.2 OASIS文件是用BNF语法定义的。下面是它的定义语法。(BNF语法请自行google学习.)
<oasis-file> -> <magic-bytes> START { CBLOCK | PAD | PROPERTY | <cell> | <name> }* END
<name> -> { CELLNAME | TEXTSTRING | LAYERNAME | PROPNAME | PROPSTRING | XNAME }
<cell> -> { CELL { CBLOCK | PAD | PROPERTY | XYRELATIVE | XYABSOLUTE | <element> }* }
<element> -> { <geometry> | PLACEMENT | TEXT | XELEMENT }
<geometry> -> { RECTANGLE | POLYGON | PATH | TRAPEZOID | CTRAPEZOID | CIRCLE | XGEOMETRY }
6.3 一个OASIS文件可以表示一个完整的分层线路(layout)图,或者部分线路图,或者多个分层线路图。
这些表示(是一个完整的hierachy layout,还是部分,或者是多个)并不是固定的,它取决于应用程序如何管理解读这些文件。每个OASIS文件必须是语法完整的。它必须用<magic-bytes> 字段开始,并且至少包含一个START 和END 记录块。.
6.4 <magic-bytes> 元素是一个13个 ASCII 字符的字节流,协议规定是: “%SEMI-OASIS<CR><NL>”, 这里的<CR><NL>表示 ASCII 字符里的 0D 0A. <magic-bytes>提供了一个可识别的签名, unix 文件可以根据这个元素用来识别文件类型。 里面的换行符则可以保证FTP程序是按照binary的模式来操作这个文件, 如果是按照non-binary模式来操作这个文件,程序遇到这个换行符则会corruption. (译者注:在这个字段,各个厂商可能会有不同,可能厂商会加上自己的log。 )
6.5 异常处理: OASIS 处理程序遇到任何无法解释的语法错误,都应该当作一个致命错误而应当退出。OASIS处理程序并不需要预先对整个文件进行检查以保证整个文件有效。如果OASIS处理程序能够并且只需要读取部分文件信息,那么只要它能正确解析自己读取的那部分信息就可以,并不需要对整个文件进行检查。
7. DATA CONSTRUCTS
不同于普通的计算机编程语言的数据格式,oasis作为一种流格式文件,有自己的数据类型表示方法。这里对其中内容进行部分说明,以便方便查阅。一共有下面几种类型的数据格式:
Table 1 oasis数据格式
| 类型 | 长度 | 其他说明 | |
| bytes | 8bit | 最低位bit放在最右边 | |
| integers | unsigned-integer | 不定,N个byte,8个bits中只有7bits表示实际数据,每个byte最高一个bit表示后面是否还有数据。0表示自己是最后一个byte。 | 最低位byte放在oasis文件的最前面 |
| signed-integer | 不定,N个byte,8个bits中只有7bits表示实际数据,每个byte最高一个bit表示后面是否还有数据。0表示自己是最后一个byte。符号位放在最低位byte(文件中最先出现的byte)的最后一位(bit):0表示正,1表示负。 | 最低位byte放在oasis文件的最前面 | |
| real | 不定。有8种表示方式。由一个unsigned-integer的数据来表示采用何种表达方式。 | 表示数据表达方式的unsigned-integer数据出现在文件的最前面。接着它后面才是实际要表达的数值。 | |
| string | 由一个unsigned-integer的数据来表示string的长度 | unsigned-integer数据出现在文件最前面。string可以分成b-string, a-string和n-string三类 | |
| deltas | delta是用来表示方向和长度的一种数据类型。分成4类。各类长度不一样。 | 在oasis文件中,这种数据的第一个出现的字节的最后几个bit是表示方向。后面具体描述。 | |
| repetitions | 用来表示重复出现的各个图形的位置的一种数据类型。也分成多类,各类长度不一。 | 在后面具体说明 | |
| point lists | 利用这个数据结构就可以画出图形。但这个数据结构本身不包括画图的起始位置信息。而在其他地方确定。是一串delta信息,用来表示各条边的长度和方向。图形的顶点越多,长度越长。 | 在后面具体说明。 | |
| property value | 由一个unsigned-integer表示类型,加上后面的property value 值构成。 | 各种类型的属性,value值不一样,但都比较简单。可以参看参考文献的7.8节table9。 | |
7.1 BYTES
7.1.1 一个Byte是固定长度的8bit数据。最低位bit放在最右边。( least significant bit (bit 0) on the
right.)
7.2 INTEGERS
OASIS文件中的整数是没有长度限制的。是长度大于0字节的一个整数。
(译者备注:虽然标准中没有整数的长度限制,但具体程序实现的时候应该使用64bits的长度来表示整数。32bits明显在EUV时代是不够的,但高于64bits也没必要。首先很多的运算库不支持长于64bits的整数,这个限制了我们可以使用的的计算精度;其次我们知道硅晶体的单个硅原子立方体长度大概是0.543nm, 如果使用64bits长度来表示坐标,如果按照硅晶体的原子长度,可以表示的长度大概是10000KM, 这个几乎是地球的直径了,所以64bits是足够使用了; 最后如果高于64bits也带了性能的影响。在实际计算中,基本都是用64bits的整数来表示整数,永远不要使用没法用64bits长整型来表示的整型数据,虽然协议本身并没有这样的限制。)
7.2.1 An unsigned-integer
低byte放在文件前面,高byte放在文件后面。
每个byte最高一个bit表示后面是否还有数据。0表示自己是最后一个byte。不定,N个byte,8个bits中只有7bits表示实际数据,每个byte最高一个bit表示后面是否还有数据。0表示自己是最后一个byte。剩下的7bits数据串在一起组成二进制数表示实际的数据。


译者注释:
unsigned-integer的长度不确定,如果数据长度有N个byte,每个byte的8个bits中只有7bits表示实际数据,最高一个bit表示后面是否还有数据。0表示自己是最后一个byte。最低位byte放在oasis文件的最前面。
举个例子就清楚了。
十进制的16383:
正常的2进制表示是:11,1111,1111,1111,一共14个1。
在oasis文件中,由于只有7位能代表实际的数,所以我们把它写成x111,1111,y111,1111。还是14个1。但中间插入了一个x和y用来表示是否后面还有数据。由于低字节优先,所以我们写成y111,1111,x111,1111。然后将y变成1,x变成0。所以最后在oasis文件中的表示是1111,1111,0111,1111。
十进制的16384:
正常的2进制表示是:100,0000,0000,0000,1后面一共14个0。
在oasis文件中,由于只有7位能代表实际的数,所以我们把它写成x000,0001,y000,0000,z000,0000。1后面还是14个0。但中间插入了一个x、y和z用来表示是否后面还有数据。由于低字节优先,所以我们写成z000,0000,y000,0000, x000,0001。然后将z变成1,y变成1,x变成1,。所以最后在oasis文件中的表示是1000,0000,1000,0000, 0000,0001。
7.2.2 signed-integer
N(N>0)个byte,8个bits中只有7bits表示实际数据,每个byte最高一个bit表示后面是否还有数据。0表示自己是最后一个byte。符号位放在最低位byte(文件中最先出现的byte)的最低一位(bit):0表示正,1表示负。+0和-0在处理的时候需要认为是相等的。
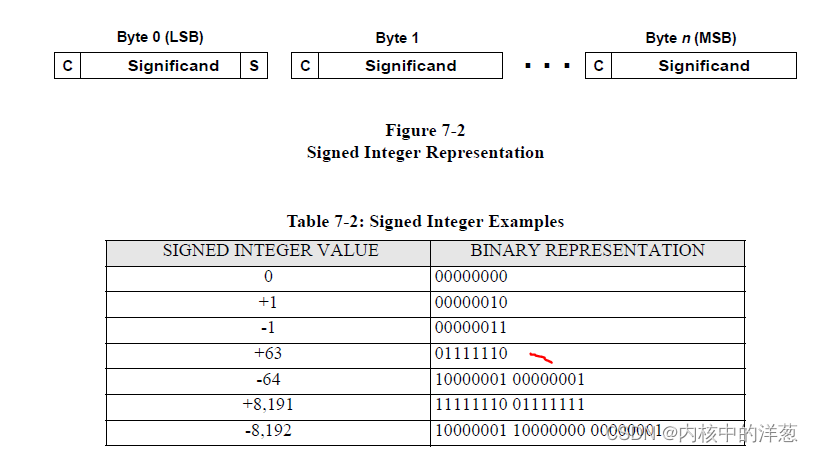
译者注释:
知道了unsigned-integer以后,再变signed-integer就简单了。还是举两个例子。
十进制的8191,
正常的2进制表示是: 1,1111,1111,1111,一共13个1。
在oasis文件中,由于第一个byte只有6位能代表实际的数,后面的byte有7位能代表实际的数。所以我们把它写成x111,1111,y111,111z。还是13个1。但中间插入了一个x和y用来表示是否后面还有数据,插入了一个z作为符号位。由于低字节优先,所以我们写成y111,111z,x111,1111。然后将y变成1,x变成0。由于是正数,所以z为0。所以最后在oasis文件中的表示是1111,1110,0111,1111。
十进制的-8192,
先表示十进制的8192,正常的2进制表示是: 10,0000,0000,0000,1后面一共13个0。
在oasis文件中,由于第一个byte只有6位能代表实际的数,后面的byte有7位能代表实际的数。所以我们把它写成m000,0001,x000,0000,y000,000z。1后面还是13个0。但中间插入了一个x和y用来表示是否后面还有数据,插入了一个z作为符号位,前面补了一个m。由于低字节优先,所以我们写成y000,000z,x000,0000,m000,0001。然后将y变成1,x变成1,m变成0。由于是负数,所以z为1。所以最后在oasis文件中的表示是1000,0001,1000,0000,0000,0001。
7.2.3 异常处理
如果有些处理器只能支持有限长度的整数,例如只能支持32bits, 如果遇到超过这个长度的整数,应该按fatal错误处理。也就是程序应该退出。
7.3 REALS
7.3.1 实数可以存放在下面的其中一种或者多种的有理数格式里面, 或者用单精度(single-precision)4bytes的(IEEE-4)或者双精度(double precision)的8bytes(IEEE-8)里面。(译者注:协议中一共列出了8种表示方法,其中前面六种是有理数的表示方法,再加上IEEE-4和IEEE-8两种。)
有理数的格式比浮点数的格式具有更高的压缩率, 而且可以具有比浮点数更高的精度。采用哪种表示方法,是由一个无符号整型来表示,这个整型在表示具体数据的实数前面。

上表 table 7-3 翻译成中文大概就是下表的含义。
Table 2 real数据类型说明
| 类型格式 | 含义 |
| 0+unsigned-integer | 是一个正的整数,整数的值就等于后面unsigned-integer |
| 1+unsigned-integer | 是一个负的整数,整数的绝对值就等于后面unsigned-integer |
| 2+unsigned-integer | 是一个正的实数,实数的值就等于后面unsigned-integer的倒数。 |
| 3+unsigned-integer | 是一个负的实数,实数的绝对值就等于后面unsigned-integer的倒数。 |
| 4+unsigned-integer1+ unsigned-integer2 | 是一个正的实数,实数的值就等于(unsigned-integer1/ unsigned-integer2)。(做除数) |
| 5+unsigned-integer1+ unsigned-integer2 | 是一个负的实数,实数的绝对值等于(unsigned-integer1/ unsigned-integer2)。(做除数) |
| 6+IEEE-4-byte-float | 表示后面是IEEE-4-byte-float的数据格式 |
| 7+IEEE-8-byte-float | 表示后面是IEEE-8-byte-float的数据格式 |
7.3.2 对于Type 0和1 , 这个实数实际是个整数,它的小数部分是0。 对于type2和type3, 表示是一个倒数。对于type 4和5表示是一个分数。 Type6和7表示是浮点数,遵循IEEE 754-1985的协议标准, 低端字节在前。
协议中给出了几个例子。见下图截图。

7.3.3 异常处理: 对于类型2-5, 如果分母是0, 应该当作fatal error 处理。 如果类型不在0-7的范围, 也应该当作fatal error处理。
译者注: 从数学角度看,这里用分数来表示有理数,确实可以表示任何一个有理数,而且由于OASIS的整数是不限制长度的,所以可以不损失精度的表示任何有理数。但从数值计算的角度考虑,计算机基本都是用浮点数表示,所以实际上最后还是转化成double型的浮点数来计算。所以从实用的角度看,用type6和type7就够了。
7.4 STRINGS
7.4.1 String 类型
string数据类型是一个复合的数据类型,它由一个表示字符串长度的unsigned-integer类型数据做为开头,后面加上真正的字符串。用BNF语法表示就是:
string -> length byte*
字符串可以分成三种:b-string(binary string), a-string(ascii string)和 n-string (name string).
b-string后面可以接任何8bits的字符编码。 a-string包括可打印的ascii字符(字符ascii的16进制编码范围0x21-0x7E)和空字符(0x20)。 n-string只包含可打印字符(ascii编码0x21-0x7E)并且长度大于0.
7.4.2 ascii编码0x21 -0x7E包含的字符有以下这些
!"#$%&’()*+,-./0123456789:;<=>?@ [21-40]
ABCDEFGHIJKLMNOPQRSTUVWXYZ[\]^_‘ [41-60]
abcdefghijklmnopqrstuvwxyz{|}~ [61-7E]
这些是不包括空格和tab字符以及一些控制字符。
7..4.3 异常处理:如果在a-string和n-string中出现了非法的字符(译者注:不在范围之内的字符), 应该认为是fatal error。 如果n-string长度是0也认为是fatal error。
7.5 DELTAS
7.5.1 delta数据类型表示的是几何数据。表示坐标,方向和偏移等信息。其中分成4种:1-delta, 2-delta, 3-delta和g-delta。分别进行说明。
7.5.2 1- delta
1-delta是一种signed-integer的数据结构,用来表示水平或者垂直方向的位置(displacement)。其中signed-integer中的符号位就用来表示方向了;singed-integer中的表示数值的部分就用来表示长度。最低一个byte的最低bit位: 0表示东或者北方向; 1表示西或者南方向。水平还是垂直对齐要根据具体场景来确定。
我们举个例子。比如二进制的1111,1001, 0010, 0011。其中第一个方框中的1和singed-integer的含义一样,表示后面还有数据。第二个方框中的1在signed-integer中表示正负符号,这里就表示方向,1表示向西或者向南(在正交坐标系中表示x和y轴的负方向,具体是x轴还是y轴由这个值出现的当前的场景来确定)。第三个框中的0表示这是这个signed-integer数据的最后一个byte。这个数据的长度是二进制的010,0011, 111, 100(去掉框内的数值,然后前后byte调转位置),这就是十进制的2300。因此这个数值就是表示向西(或者向南)画2300长度的一条线。
2- delta
2-delta是一种unsigned-integer的数据结构,跟1delta一样,用来表示水平或者垂直方向的位置(displacement)。 其中unsigned-integer中的最低2bits(在oasis文件中最先出现的byte中的最低2bits)用来表示方向了,其他部分表示数值的大小,数值的大小就用来表示长度。
我们举个例子。比如二进制的1001,1000, 0010, 1010。其中第一个方框中的1和unsinged-integer的含义一样,表示后面还有byte表示同一个unsigned-integer数据。第二个方框中的00这里就表示方向,00表示向东(在正交坐标系中表示x正方向,01表示向北,10表示向西,11表示向南)。第三个框中的0表示这是这个unsigned-integer数据的最后一个byte。这个数据的长度是二进制的010,1010, 001, 10(去掉框内的数值,然后前后byte调转位置),这就是十进制的1350。因此这个数值就是表示向东(就是从当前位置,向x轴正方向)画长度1350的一条线。
3- delta
3-delta是一种unsigned-integer的数据结构,用来表示水平、垂直或者45°方向的位置(displacement)。其中unsigned-integer中的最低3bits(在oasis文件中最先出现的byte中的最低3bits)用来表示方向了,其他部分表示数值的大小,数值的大小就用来表示x轴和y轴的偏移长度。
我们举个例子。比如二进制的1100,1101, 0000, 0001。其中第一个方框中的1和unsinged-integer的含义一样,表示后面还有byte表示同一个unsigned-integer数据。第二个方框中的101这里就表示方向,101表示西北方向(在正交坐标系中表示135度角的一条线,000表示向东,001向北,010表示向西,011表示向南,100表示东北方向,110表示西南方向,111表示东南方向)。第三个框中的0表示这是这个unsigned-integer数据的最后一个byte。这个数据的长度是二进制的000,0001, 100, 1(去掉框内的数值,然后前后byte调转位置),这就是十进制的25。因此这个数值就是表示向西北方向(就是从当前位置,向135度角方向)画长度为sqrt(25*25+25*25)的一条线(x轴偏移25,y轴偏移25)。
g- delta
g-delta有两种形式,一种是用一个单一的unsigned-integer的数据来表示;第二种是用一对unsigned-integer的数据来表示。如果g-delta数据在文件中第一个出现的字节的最低位(bit0)是0,表示第一种类型的g-delta数据;如果是1,表示第二种类型的g-delta数据。
g- delta 第一种类型
如果是第一种类型,只用一个unsigned-integer类型表示g-delta的类型。unsigned-integer的在文件中出现的第一个字节的倒数第2到第4个bit(bit1到bit3)一共3个bits用来表示方向,同3-delta的形式。
举个例子,二进制的1110,1100,0000,0101。其中第二个方框中的0表示这是第一种类型的g-delta格式,第一个方框中的1和unsinged-integer的含义一样,表示后面还有byte表示同一个unsigned-integer数据。划下划线的110这里就表示方向,110表示西南方向(在正交坐标系中表示135度角的一条线,000表示向东,001向北,010表示向西,011表示向南,100表示东北方向,101表示西北方向,110表示西南方向,111表示东南方向)。第三个框中的0表示这是这个unsigned-integer数据的最后一个byte。这个数据的长度是二进制的000,0101, 110(去掉打框的和加下划线的数值,然后前后byte调转位置),就是十进制的46。整个数据的含义就是沿西南方向画一条长度为sqrt(46×46+46×46)的线(也是就是将x轴坐标减少46,y坐标减少46,将这个点作为顶点,和原来坐标点相连画一条直线)。
g- delta 第二种类型
如果是第二种类型,则用两个unsigned-integer的数据来表示。第一个unsigned-integer在文件中的第一个byte的最低bit(bit0)必须为1,第一个byte的倒数第二个bit(bit1)表示x轴的方向,其它bit表示长度。第二个unsigned-integer在文件中的第一个byte的最低bit(bit0)表示y轴的方向,其它bit表示长度。因此,它能够表示任何方向的线段。只有这种数据能够表示任何方向任何角度的线段,其它delta的类型都只能表示45度或者90度方向的线段。
举个例子,二进制的1011,1011,0000,0001,1011,0111,0000,1111。
其中第二个方框中的1表示这是第二种类型的g-delta格式,第一个方框中的1和unsinged-integer的含义一样,表示后面还有byte表示同一个unsigned-integer数据。划下划线的1这里就表示方向,1表示向西(x轴负方向,0表示向东)。第三个框中的0表示这是第一个unsigned-integer数据的最后一个byte。这个数据的长度是二进制的000,0001, 011,10(去掉打框的和加下划线的数值,然后前后byte调转位置),就是十进制的46。整个数据的含义就是x轴沿负方向减少长度46,取一条和y轴平行的直线。后面y轴也取一条和x轴平行直线,两者相交得到一个点。整个delta就是从当前位置到这个点画一条直线。
第四个方框中的1和unsinged-integer的含义一样,表示后面还有byte表示同一个unsigned-integer数据。第六个框中的0表示这是第二个unsigned-integer数据的最后一个byte。第五个框中的 1就表示方向,1表示向南(y轴负方向,0表示向北)。整个数据的含义就是y轴沿负方向减少长度46,取一条和x轴平行的直线。
原协议给出了一些delta的数据的例子,放在下图中。
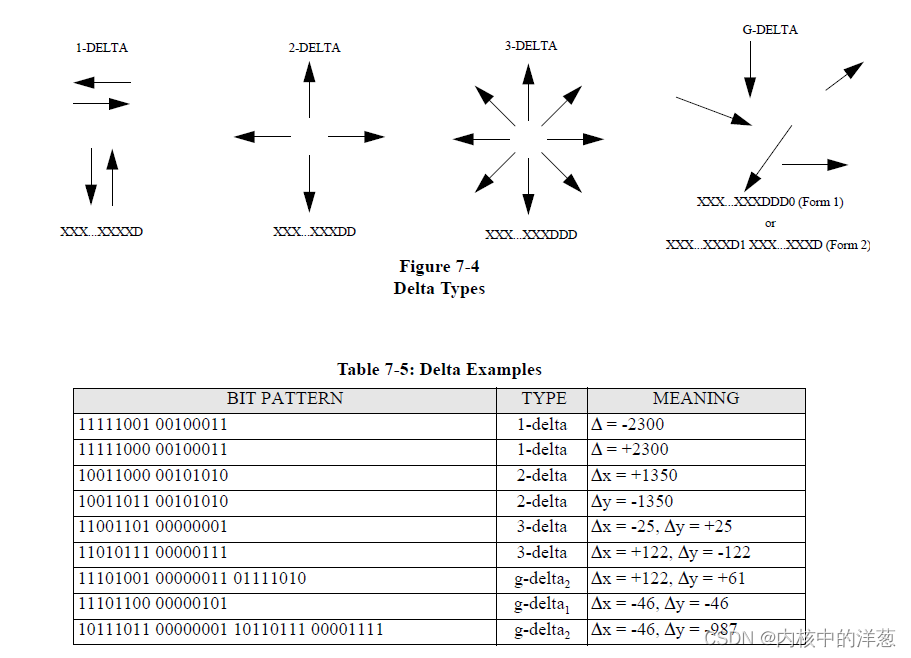
7.6 REPETITIONS
7.6.1 repetition 用来表示一个cell, 一个几何图形或者一串文本的重复排列方式。Repetition是
PLACEMENT, <geometry>, 或者TEXT record 本身的一部分。 Repetition 由一个表示repetition类型的无符号整数,后面跟着跟repetition相关的参数组成。
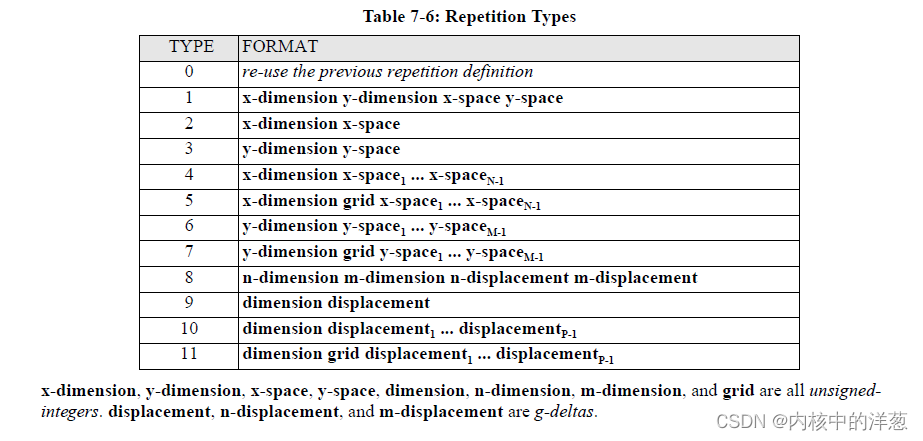
译者备注:
在光刻版图中,一个相同的图形常常在多个位置重复出现。repetition就用来表示图形重复出现的位置。repetitions其本质是分成三部分,第一部分表示类型,用一个unsigned-integer的数据来表示,一共有12种类型,就是table 7-6中的type。 第二部分表示维数,就是7.6节中table 7-6中的dimension,它表示了这个图形重复出现的次数;第三部分是表示位置,就是各个重复出现的图形应该出现在版图中的哪个位置,中7.6节中table 7-6中的space和displacement。
Repetition的各种类型的说明。原协议的描述见下图。

下面这张表是译者对各种repetition进行一些注释说明。
Table 3 repetitions类型说明
| 类型 | format | 位置坐标 |
| 0 | 参见上面Table 7-6 | 重复上一次repetition的数据。根据上一次repetition的类型和数据来重复本图形的计算。比如上次是类型1的repetition,那么现在也是类型1的repetition,并且dimension和space参数也相同 |
| 1 | 参见上面Table 7-6 | x-dimension=N-2, y-dimension=M-2. 生成一个N列M行的矩阵,矩阵中每个元素表示一个重复的图案。元素element(i , j )(i=0 , ... , N-1, j= 0, ..., M-1)的位置为(i*x-space, j*y-space)。 用来生成x轴和y轴平行的重复图案。 |
| 2 | 参见上面Table 7-6 | x-dimension=N-2,生成一个N列1行的矩阵。矩阵中每个元素表示一个重复的图案。元素element(i)(i=0 , ... , N-1)的位置为(i*x-space, 0)。 用来生成和x轴平行的重复图案。 |
| 3 | 参见上面Table 7-6 | y-dimension=M-2,生成一个1列M行的矩阵。矩阵中每个元素表示一个重复的图案。元素element(j)(j=0 , ... , M-1)的位置为(0, j*y-space)。 用来生成和y轴平行的重复图案。 |
| 4 | 参见上面Table 7-6 | x-dimension=N-2,生成一个N列1行的矩阵。矩阵中每个元素表示一个重复的图案。元素element(i)(i=0 , ... , N-1)的位置为(x-space0+ x-space1+...+ x-spacei, 0),其中x-space0=0。 用来生成和x轴平行的重复图案。 |
| 5 | 参见上面Table 7-6 | 跟类型4类似,x-dimension=N-2,生成一个N列1行的矩阵。矩阵中每个元素表示一个重复的图案。元素element(i)(i=0 , ... , N-1)的位置为(grid*(x-space0+ x-space1+...+ x-spacei), 0),其中x-space0=0。 用来生成和x轴平行的重复图案。 |
| 6 | 参见上面Table 7-6 | y-dimension=M-2,生成一个1列M行的矩阵。矩阵中每个元素表示一个重复的图案。元素element(j )(j=0 , ... , M-1)的位置为(0, y-space0+ y-space1+...+ y-spacej),其中y-space0=0。 用来生成和y轴平行的重复图案。 |
| 7 | 参见上面Table 7-6 | 跟类型6类似,y-dimension=M-2,生成一个1列M行的矩阵。矩阵中每个元素表示一个重复的图案。元素element(j )(j=0 , ... , M-1)的位置为(0, gird*(y-space0+ y-space1+...+ y-spacej) ),其中y-space0=0。 用来生成和y轴平行的重复图案。 |
| 8 | 参见上面Table 7-6 | n-dimension=N-2, m-dimension=M-2. n-displacement(m-displacement类似这样处理)是g-delta类型的数据,含有长度和方向信息,可以把g-delta数据分成两部分nx-space和ny-space,分表表示x轴方向的偏移和y轴方向的偏移。g-delta可以表示任意角度的方向。 整个数据生成一个N列M行的矩阵,矩阵中每个元素表示一个重复的图案。元素element(i , j )(i=0 , ... , N-1, j= 0, ..., M-1)的位置为(i*nx-space+j*mx-space, i*ny-space+j*my-space)。 用来生成沿对角方向(不一定是45度角)的重复图案。 |
| 9 | 参见上面Table 7-6 | dimension=P-2,生成一个P维的向量。向量中每个元素表示一个重复的图案。元素element(k)(k=0 , ... , P-1)的位置为(k*x-space, k*y-space), 用来生成沿对角方向的P维重复图形的图案。 |
| 10 | 参见上面Table 7-6 | dimension=P-2,生成一个P维的向量。向量中每个元素表示一个重复的图案。元素element(k)(k=0 , ... , P-1)的位置为(x-space0+x-space1+...+x-spacek, y-space0+y-space1+...+y-spacek), 它可以用来生成沿任何方向任何位置的P维重复图形的图案。 |
| 11 | 参见上面Table 7-6 | 跟类型10类似,dimension=P-2,生成一个P维的向量。向量中每个元素表示一个重复的图案。元素element(k)(k=0 , ... , P-1)的位置为 (grid*(x-space0+x-space1+...+x-spacek), grid*( y-space0+y-space1+...+y-spacek)), 它可以用来生成沿任何方向任何位置的P维重复图形的图案。 |
下面是各种repetition的例子说明。

7.6.14 异常处理: 如果repetition的类型不在0-11范围之内,那么因为认为是一个fatal error。 Type 为0的repetition 不应该是一个cell里面的第一个repetition类型。
7.7 POINT LISTS
7.7.1 point-list 数据类型是用来表示多边形(polygons)或者paths的几何坐标。 它有五种类型的表示方式, 由一个无符号整数来表示它的类型。它的结构是首先由一个无符号整数表示它的类型,然后接着一系列的delta数据。 一个polygon或者path的初始顶点坐标(x,y) 是在POLYGON 或者PATH record 里面指定它并不是point-list数据结构中的一部分。顶点的个数 vertex-count是一个unsigned-integer, 表示的是points的个数或者deltas的个数, 这个vertex-count并不包括初始顶点,也不包括隐藏并没有明确说明的顶点。
这里列出了五种point-list的结构。



译者解读:
point list数据类型是用来画图形的,他可以画出边为直线的任意多边形的图形。point lists有五种类型。其结构可以分成三部分:第一部分表示类型,就是point list 类型;第二部分表示顶点的个数,用一个unsigned-integer类型表示;第三部分用delta表示多边形的边长度以及方向,由一串delta构成,每一个delta表示了多边形的一条边。
图形的起始位置并不包含在point lists数据结构中,图形的起始位置由POLYGON记录和PATH记录中的相关信息给出。
这里不对point list五种类型的数据格式进行具体说明,可以参考上面的table7-7 以及7.7.2到7.7.7节的说明。这里只对表中特别容易混淆或者不清楚的地方进行一些说明。
- 表中的vertex-count并不是表示顶点的个数,而是表示后面delta类型的数据的个数。有些多边形的边并不需要用delta来表示,比如最后一条边,总可以将起始顶点和最后顶点直接相连来得到。
- 表中所谓manhattan 就是指多边形图形的边只平行x轴或者y轴方向,而不会沿其他方向。
- 所谓octangular是指多边形的边只平行x轴或者y轴方向,或者与他们形成45度角方向,而不会沿其他方向。如果不是沿45度角认为出错。
- all-angle则表示多边形的边可能沿任何角度任何方向。
我们可以看几个例子,就拿上面的table 7-8和figure7-6为例子。Figure7-6和table7-8是对应的, figure7-6是根据table7-8中的数据画出来的。我们拿type 3为例,其他类似就不重复了。在Figure7- 6 中,(x,y)是表示画图的起始位置,虚线表示缺省暗示的线(这里的顶点不会统计在point-list 的vertex-count里面),不会在delta数据中体现出来。。
type3中,对应table7-8中的bit pattern为00000011,00000100,00010101,00100001,00110000, 00010011。首先第一个byte为00000011值为3表示类型3,对应table 7-7,可以看到后面是3-delta类型的数据。第二个byte为00000100值为4,表示后面有4个3-delta的数据。第三个byte为00010101,对照3-delta的数据格式,可以看到这是一个沿西北方向的线,长度为二进制的1010,也就是十进制的10。第三个byte为00010101,对照3-delta的数据格式,可以看到这是一个沿西北方向的线,这个3-delta数值大小为二进制的10,也就是十进制的2,所以线的长度为sqrt(2×2+2×2)。第四个byte为00100001,对照3-delta的数据格式,可以看到这是一个向北方向的线,这个3-delta数值大小为二进制的100,也就是十进制的4,所以线的长度为sqrt(4×4+4×4)。以此类推,最后一条线是缺省暗示的,将最后的一个点和起始点相连即可得到最后的一条直线(图上的虚线)。
7.7.8 异常处理:如果point-list的类型不在[0-5]之间,认为是fatal error. For point-list types 0-1, successive coincident points and/or adjacent colinear edges are not permitted. A non-manhattan
implicit closing vector for a polygon using point-list type 2, or a non-octangular implicit closing vector for a polygon using point-list type 3 should be treated as a fatal error. For polygons using point-list types 0-1, a vertex count which is odd or less than 2 should be treated as a fatal error.
7.8 PROPERTY VALUES
7.8.1 属性值( property-value) 存放的是一个元素的属性值列表。它首先也是由一个表示类型的无符号整型开头,后面接着属性值本身或者一个引用号(reference number)。 属性值的表示有8中类型,用 Types 0-7 表示。
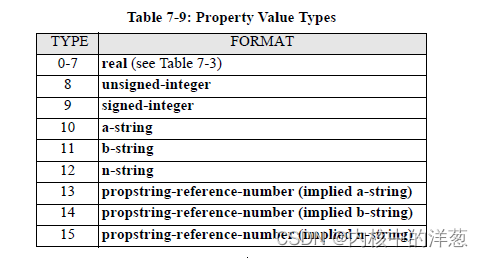
7.8.2 异常处理: 如果属性值不在[0-15]之间,认为是fatal error。 如果用propstring-reference-number 表示属性值,但是在同一个OASIS文件中在 PROPSTRING record中里面,并没有找到对应的引用号,那么认为是fatal error。
译者备注: 其实引用可以用引用号,也可以用element的名字来引用。但在实际中请严格使用引用号来做引用,而不要使用名称。
译者备注:
到这里,终于把OASIS标准中的数据结构讲完了。后面就讲6.2节里提到的BNF语法中提到的各个组成单元的定义了。开始之前最好重温一下6.2节的内容。