算法设计与分析复习01:主方法求递归算法时间复杂度
文章目录
- 算法设计与分析复习01:主方法求递归算法时间复杂度
- 复习重点
- 算法复杂度分析——主方法
- 例题1:
- 例题2:
- 例题3:
复习重点

算法复杂度分析——主方法
T ( n ) = a T ( n b ) + f ( n ) T(n)=aT(\frac{n}{b})+f(n) T(n)=aT(bn)+f(n)
- 其中
a≥1和b>1是常数,f(n)是渐进函数 。 - 上述递归式描述的是这样一种算法的运行时间:
- 它将规模为
n的问题分解为a个子问题 每个子问题规模为 n b \frac{n}{b} bn ,其中a和b都是正常数。 - a 个子问题递归地进行求解,每个花费时间 T(n/b) 。
- 函数 f(n) 包含了问题分解和子问题解合并的代价 。
- 其中 n b \frac{n}{b} bn 指 n b \frac{n}{b} bn 的上取整或者是下取整,对结果不会造成影响。
- 它将规模为

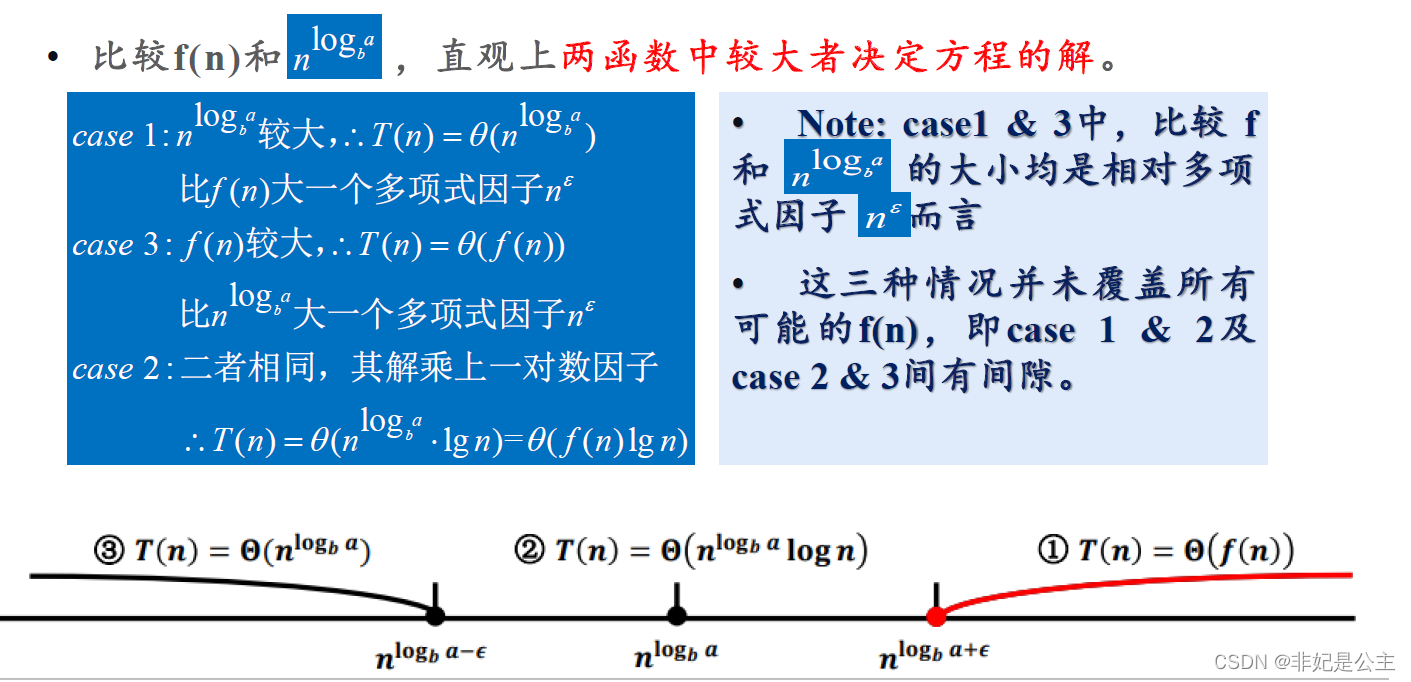
例题1:

例题2:

例题3: