目录

一、算法介绍

二、算法描述

三、算法总结

---

一、算法介绍

  Cohen–Sutherland 算法用于直线段裁剪，通过判断直线与窗口之间的关系，来决定直线段部分的保留与舍弃。

二、算法描述

  ① 首先，我们把屏幕分割成 9 个区域块，最中间区域块是窗口(裁剪面)，其余 8 个区域块在它周围。我们用 4 位二进制来标记每个区域块：

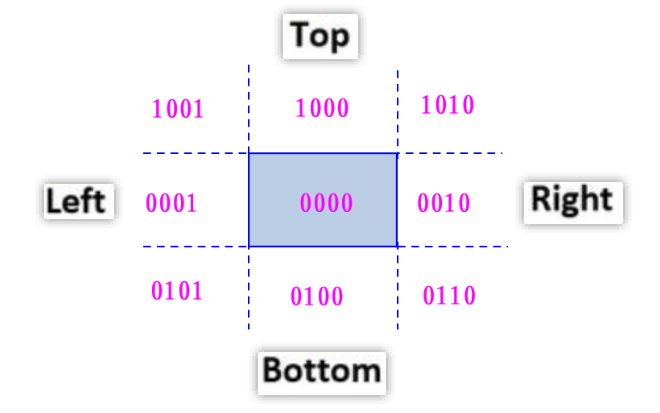
关于4位二进制的表示法 ，参考图如下：

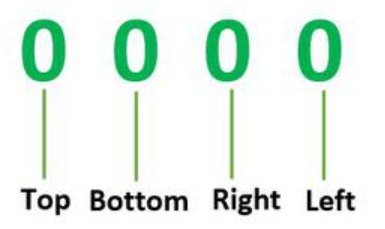
 第1位，如果该区域块位于Top域，则为1，否则为0；

 第2位，如果该区域块位于Bottom域，则为1，否则为0；

 第3位，如果该区域块位于Right域，则为1，否则为0；

 第4位，如果该区域块位于Left域，则为1，否则为0；

② 接下来就是对于各种不同类型待裁剪线段的区分。比方说有以下若干线段：

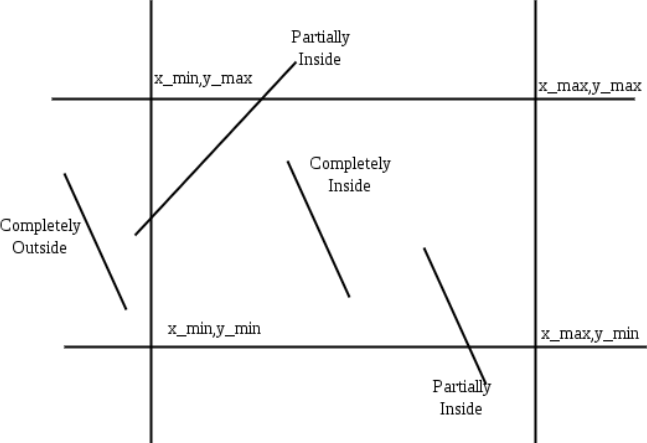
  我们根据线段两端点位于的区域块位置来区分线段类型，可总结出以下三种类型的线段：

A、Completely inside：线段两端点都在窗口内。

B、Completely outside：线段两端点都在窗口外。

C、Partially inside：线段一个端点在窗口内，一个端点在窗口外。

③ 那么如何通过算法来区分出以上三种线段类型呢？方法如下：

  设线段两端点分别为C1，C2。

  如果两端点区域块代码都是0000，则对应类型A，保留线段；

  否则将端点C1和C2执行逻辑与运算，如果结果不是0000，则线段两端点一定都在窗口外，对应类型B，不保留线段；

  否则如果两端点区域块代码不都是0000，但逻辑与后结果是0000，则对应类型C，需要对线段进行求交裁剪操作。

④ 对C类型线段进行求交裁剪。方法很简单，将C类型线段与裁剪面的四个边界依次进行求交即可，步骤如下图：

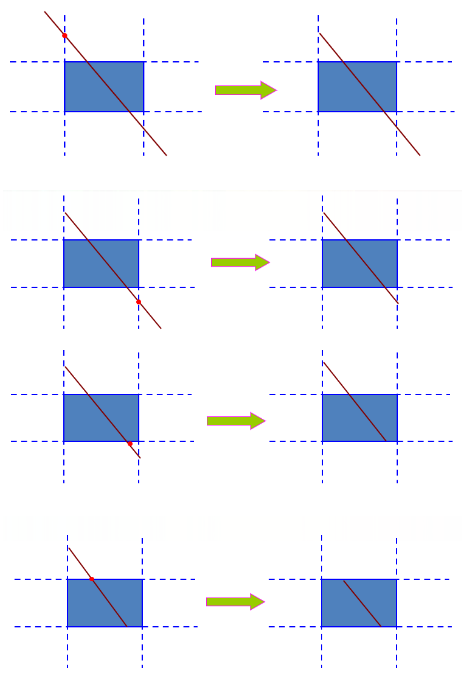
三、算法总结

  Cohen–Sutherland 算法伪代码如下：

第 1 步：为给定线段的两个端点分配4位二进制区域代码。
第 2 步：如果两个端点的区域代码都是0000，则表明线段完全在窗口内。
第 3 步：否则，对两个区域块代码执行逻辑与运算{
    如果结果不是0000，那么线段全在窗口外部，
    else 如果结果是0000，表明线段部分位于窗口内部{
         找到线段与窗口的交点，
         用交点替换线段的端点，并更新4位二进制区域代码，
         重新回到第 2 步，一直到剪裁完成再退出。
    }
}