费解的开关(BFS+哈希表+二进制枚举)
- 一、题目
- 二、思路分析
- 1、算法标签
- 2、思路梳理
- 方法1:BFS+哈希表
- 方法2:二进制枚举+DFS
一、题目

二、思路分析
1、算法标签
这道题考察的是BFS+哈希表,DFS+二进制枚举
2、思路梳理
方法1:BFS+哈希表
这道题的思路和作者之前讲解的八数码的问题是很接近的思路。
如果大家不了解那道题的话,作者建议大家去看一看那道题,二者的思路是一样的。传送门:
八数码(BFS+哈希)
在讲解方法一的思路之前,我们先来做一下铺垫:
这道题的题面给出了一个二维矩阵,又问的是最小操作次数问题,那么我们很容易联想到利用搜索处理。
但是搜索的话,我们并不是在题目给出的一个二维矩阵里进行不断地变化。
我们是把一个二维矩阵看作一个点,而点与点之间的边其实就是二维矩阵发生变化时的操作。
简而言之,我们不是将一个字符看作一个点,而是将一个状态看作一个点。
而我们如何将一个二维矩阵看成一个点呢?我们发现这道题中的矩阵是由01组成的,因此,我们可以将矩阵中的25个0或1压缩成一个二进制数字,然后将这个二进制数字转化为十进制存储起来。
然后我们的终点就是二维数组中25个数字全为1的时候,此时这个数就是 2 5 − 1 2^5-1 25−1。
我们知道这个时间复杂度是很高的,那么为了避免不断地搜索,我们可以从反面思考,我们将终点状态,即25个1的状态,看作起点,然后从这个点出发,去枚举出6次操作以内所能够形成的所有状态。然后我们用状态去索引操作次数,故为了提高索引的效率,我们采用哈希表。后续只需要根据输入查表即可。
但是,这样的时间复杂度相当高,所以我们要及时终止,由于BFS具有最短路的性质,因此当我们从队列中取出了一个操作次数为6的状态的时候,我们就可以终止了,因为后续的状态所需的操作次数都是大于等于6的。
代码如下:
#include<iostream>
#include<unordered_map>
#include<queue>
using namespace std;
int a[30];
unordered_map<int,int>dis;
int n;
int dx[4]={-1,0,1,0},dy[4]={0,1,0,-1};
void bfs()
{
queue<int>q;
int end=(1<<25)-1;
dis[end]=0;
for(int i=0;i<25;i++)
{
int j=end-a[i];
for(int k=0;k<4;k++)
{
int nx=i/5+dx[k],ny=i%5+dy[k];
if(nx>=0&&nx<5&&ny>=0&&ny<5)
{
j-=a[nx*5+ny];
}
}
q.push(j);
dis[j]=1;
}
while(!q.empty())
{
int t=q.front();
q.pop();
int distance=dis[t];
if(distance==6)return;
string s1;
for(int i=0;i<25;i++)
{
if(t>>i&1)s1+='1';
else s1+='0';
}
for(int i=0;i<25;i++)
{
int tmp=t;
string ts=s1;
int x=i/5,y=i%5;
for(int j=0;j<4;j++)
{
int nx=x+dx[j],ny=y+dy[j];
if(nx>=0&&nx<5&&ny>=0&&ny<5)
{
s1[nx*5+ny]='1'-s1[nx*5+ny]+'0';
if(s1[nx*5+ny]=='1')t+=a[nx*5+ny];
else t-=a[nx*5+ny];
}
}
s1[i]='1'-s1[i]+'0';
if(s1[i]=='1')t+=a[i];
else t-=a[i];
int d=distance+1;
if(d<=6&&(!dis.count(t)))
{
dis[t]=d;
q.push(t);
}
t=tmp;
s1=ts;
}
}
}
int main()
{
for(int i=0;i<25;i++)
{
a[i]=1<<i;
}
bfs();
cin>>n;
string s1;
while(n--)
{
int res=0;
for(int i=0;i<25;i++)
{
char c;
cin>>c;
if(c=='1')res+=a[i];
}
if(dis.count(res))
printf("%d\n",dis[res]);
else
printf("-1\n");
}
}
方法2:二进制枚举+DFS
我们发现方法一的特点就是简单粗暴,但是代码量很大,并且效率很低。
我们现在来研究一下这道题中的某些性质:
1、灯是否全亮只取决于你按了哪些灯,但是这些灯之间被按的顺序是没有用的。为什么?对于每个灯而言,他的变化也就是从不亮到亮,或者亮到不亮。这个变化只取决于这个灯原来的状态,和顺序无关。
2、最少的操作次数中,某个被按的灯一定是只被按了一次。因为如果按两次,相当于这个灯没被按,如果按奇数次的话,那这个效果和只按一次是一样的。
既然最优的方案只和按哪些灯有关,和操作之间的顺序无关的话,我们就人为的规定一下操作的顺序:
从第一层逐层向下。
我们现在看这种方式:
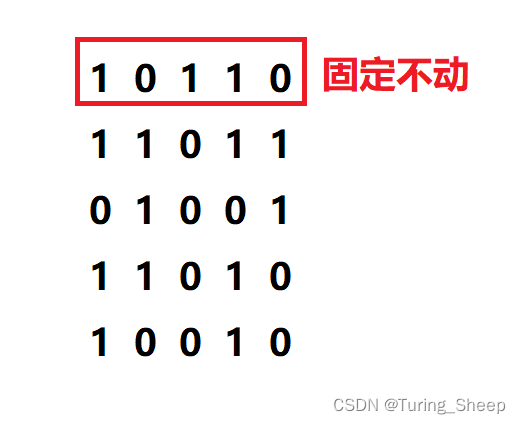
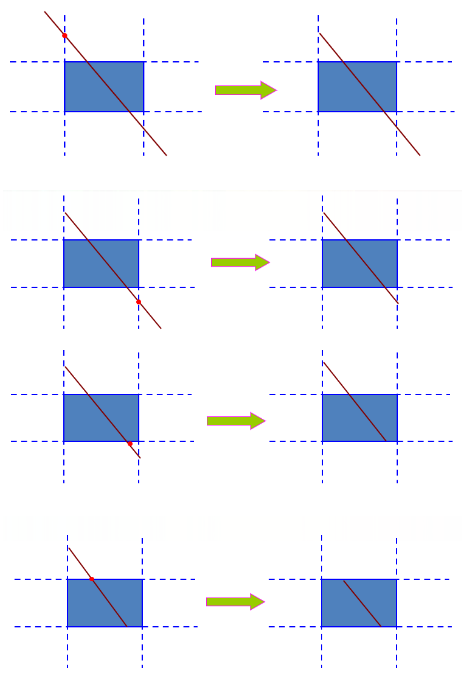
如果第一行,我们固定不变,那么能够让第一行中灭掉的灯变亮的方式只能是去按第二层对应的灯。我们可以靠第二层产生的连锁反应让第一行对应的灯变亮。
但同样的情况,我们第二行的某些亮着的灯可能也会被灭掉,因此,我们可以通过操作第三层的灯,来让第二层灭掉的灯变亮。
但是很明显,我们的最后一行是无法通过以上的方式点亮。若能够点亮的话,只能是通过倒数第二层的连锁反应让最后一层自动点亮。这样的话就是可行的操作。
但是,我们的第一行怎么按是不确定的。
而又因为按哪些灯和我们的方案有关,那么我们就需要去枚举所有方案,看看是不是存在可行的方案。而由于一个方案后续的操作完全取决于第一行,**因此我们只需要去枚举第一行的所有操作情况即可。**后续行的操作可以从第一行逐级推导出来。
而第一行的操作可能共有 2 5 2^5 25次方种可能。所以我们可以枚举从 0 0 0到 2 5 − 1 2^5-1 25−1,然后看这些数字的二进制位,如果二进制位是1,意思就是操作,二进制位是0,意思就是不操作。
#include<iostream>
#include<cstring>
using namespace std;
const int N=6;
char g[N][N],backup[N][N];
int dx[5]={-1,0,1,0,0},dy[5]={0,1,0,-1,0};
void turn(int x,int y)
{
for(int i=0;i<5;i++)
{
int a=x+dx[i],b=y+dy[i];
if(a>=0&&a<5&&b>=0&&b<5)
g[a][b]^=1;
}
}
int main()
{
int T;
cin>>T;
while(T--)
{
for(int i=0;i<5;i++)cin>>g[i];
int res=10;
for(int op=0;op<32;op++)
{
memcpy(backup,g,sizeof g);
int step=0;
for(int i=0;i<5;i++)
{
if(op>>i&1)
{
step++;
turn(0,i);
}
}
for(int i=0;i<4;i++)
{
for(int j=0;j<5;j++)
{
if(g[i][j]=='0')
{
turn(i+1,j);
step++;
}
}
}
bool dark=false;
for(int i=0;i<5;i++)
{
if(g[4][i]=='0')
{
dark=true;
break;
}
}
if(!dark)res=min(res,step);
memcpy(g,backup,sizeof g);
}
if(res>6)res=-1;
cout<<res<<endl;
}
}