应用torchinfo计算网络的参数量

news2024/9/24 11:30:41

1 问题

定义好一个VGG11网络模型后，我们需要验证一下我们的模型是否按需求准确无误的写出，这时可以用torchinfo库中的summary来打印一下模型各层的参数状况。这时发现表中有一个param以及在经过两个卷积后参数量（param）没变，出于想知道每层的param是怎么计算出来，于是对此进行探究。

2 方法

1、网络中的参数量(param)是什么？

param代表每一层需要训练的参数个数，在全连接层是突触权重的个数，在卷积层是卷积核的参数的个数。

2、网络中的参数量(param)的计算。

卷积层计算公式:Conv2d_param=(卷积核尺寸*输入图像通道+1)*卷积核数目

池化层：池化层不需要参数。

全连接计算公式：Fc_param=(输入数据维度+1)*神经元个数

3、解释一下图表中vgg网络的结构和组成。vgg11的网络结构即表中的第一列：

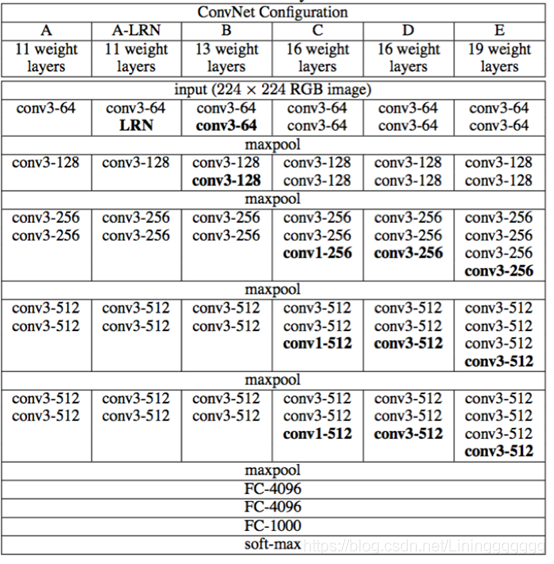conv3-64→maxpool→conv3-128→maxpool→conv3-256→conv3-256→maxpool→conv3-512→conv3-512→maxpool→conv3-512→conv3-512→maxpool→FC-4096→FC-4096→FC-1000→softmax。

4、代码展示

import torch
from torch import nn
from torchinfo import summary
class MyNet(nn.Module):
#定义哪些层
def __init__(self) :
super().__init__()
#(1)conv3-64
self.conv1 = nn.Conv2d(
in_channels=1, #输入图像通道数
out_channels=64,#卷积产生的通道数(卷积核个数)
kernel_size=3,#卷积核尺寸
stride=1,
padding=1 #不改变特征图大小
)
self.max_pool_1 = nn.MaxPool2d(2)
#(2)conv3-128
self.conv2 = nn.Conv2d(
in_channels=64,
out_channels=128,
kernel_size=3,
stride=1,
padding=1
)
self.max_pool_2 = nn.MaxPool2d(2)
#(3)conv3-256
self.conv3 = nn.Conv2d(
in_channels=128,
out_channels=256,
kernel_size=3,
stride=1,
padding=1
)
self.conv4 = nn.Conv2d(
in_channels=256,
out_channels=256,
kernel_size=3,
stride=1,
padding=1
)
self.max_pool_3 = nn.MaxPool2d(2)
#(4)conv3-512
self.conv5 = nn.Conv2d(
in_channels=256,
out_channels=512,
kernel_size=3,
stride=1,
padding=1
)
self.conv6 = nn.Conv2d(
in_channels=512,
out_channels=512,
kernel_size=3,
stride=1,
padding=1
)
self.max_pool_4 = nn.MaxPool2d(2)
#(5)conv3-512
self.conv7 = nn.Conv2d(
in_channels=512,
out_channels=512,
kernel_size=3,
stride=1,
padding=1
)
self.conv8 = nn.Conv2d(
in_channels=512,
out_channels=512,
kernel_size=3,
stride=1,
padding=1
)
self.max_pool_5 = nn.MaxPool2d(2)
self.fc1 = nn.Linear(in_features=7*7*512,out_features=4096)
self.fc2 = nn.Linear(in_features=4096,out_features=4096)
self.fc3 = nn.Linear(in_features=4096,out_features=1000)
#计算流向
def forward(self,x):
x = self.conv1(x)
x = self.max_pool_1(x)
x = self.conv2(x)
x = self.max_pool_2(x)
x = self.conv3(x)
x = self.conv4(x)
x = self.max_pool_3(x)
x = self.conv5(x)
x = self.conv6(x)
x = self.max_pool_4(x)
x = self.conv7(x)
x = self.conv8(x)
x = self.max_pool_5(x)
x = torch.flatten(x,1) #[B,C,H,W]从C开始flatten，B不用flatten，所以要加1
x = self.fc1(x)
x = self.fc2(x)
out = self.fc3(x)
return out
if __name__ == '__main__':
x = torch.rand(128,1,224,224)
net = MyNet()
out = net(x)
#print(out.shape)
summary(net, (12,1,224,224))

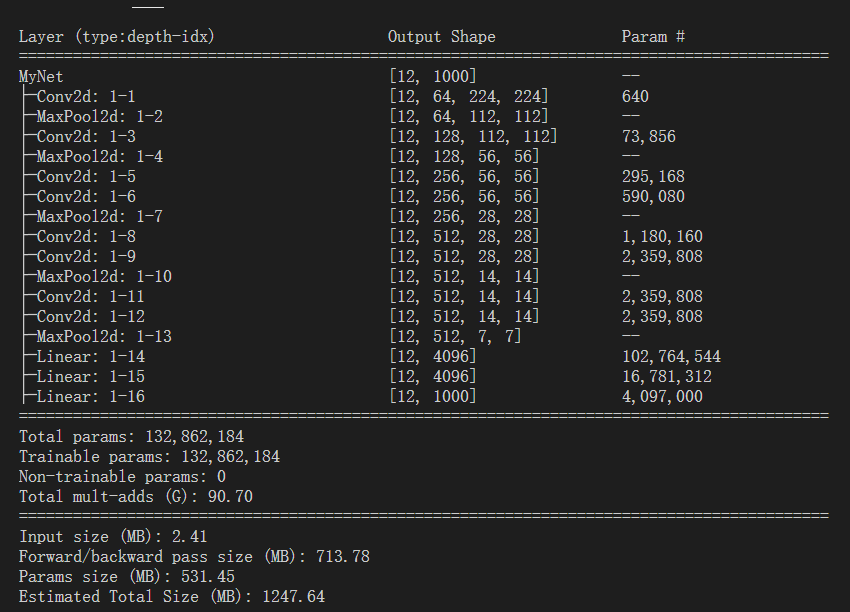输出结果：