Networkx实现小世界网络的分析

小世界网络

小世界现象，也被称为六度分离原则，即如果你在地球上的任何地方随便选择任何两个人，你会发现一条至多由他们之间的6个熟人形成的路径。在网络科学语言中，六度也被称为小世界性质，意味着网络中任何两个节点之间的距离十分小。小世界现象也意味着网络中随机选择的两个节点之间的距离很短。六度分离原理：

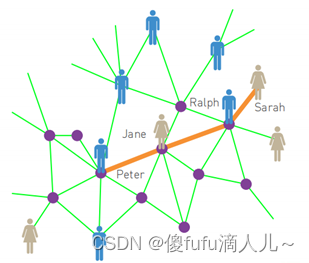
小世界网络模型是对小世界现象的网络模型建模。小世界现象中提出了网络任何两个节点之间的距离很短，那么“短”应该如何来衡量，又应该如何表示这些“短距离”呢？

可以考虑一个平均度为< k >的随机网络，设节点之间距离用 d 表示，那么对于网络中的每个节点，应当有如下性质：

➢ 有< k >个距离自身为 1（即 d=1）的节点

➢ 有< 𝑘 >2个距离自身为 2（即 d=2）的节点

➢ 有< 𝑘 >3个距离自身为 3（即 d=3）的节点

➢ 有< 𝑘 >𝑛个距离自身为 n（即 d=n）的节点

网络指标分析

网络直径

网络中任意两个节点之间的距离的最大值称为网络的直径，记为 D。实际中网络往往并不是连通的，而是存在一个连通巨片。网络直径通常是指任意两个存在有限距离的节点(也称连通的节点对)之间的距离的最大值。

平均路径长度

网络中任意两个节点距离的平均值，即为网络的平均路径长度，也称网络的平均距离，记为 L。

聚集系数

某个节点的聚集系数刻画了该节点的邻居节点中任意一对节点有连边的概率。即：

其中，𝐸𝑖为该点的邻居节点之间实际存在的边数，𝑘𝑖为该点的邻居节点个数。网络的聚集系数定义为网络中所有节点的聚集系数的平均值。即：

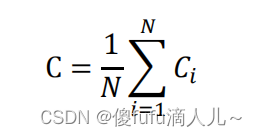
度分布

在网络中，度（degree）是指网络中一个点与其他点的连接数量。对于有向图，度有入度（in-degree）和出度（out-degree），入度是指指向该节点的边的数量，出度是指从该节点出发指向其他节点的边的数量。度分布（degree distribution）是指整个网络中，各个点的度数量的概率分布。

代码实现

import networkx as nx
import matplotlib.pyplot as plt

# WS network
NETWORK_SIZE = 100
k = 10
p = 0.1
G = nx.watts_strogatz_graph(NETWORK_SIZE, k, p)
print('网络直径为：', nx.diameter(G))
print('网络平均距离为：', nx.average_shortest_path_length(G))
print('网络群聚系数为：', nx.clustering(G))
print('网络平均群聚系数为：', nx.average_clustering(G))
# print('网络中自环的个数为：', nx.number_of_selfloops(G))
# print('网络中重边的个数为：', G.edges())

# 绘制WS小世界网络图
plt.figure()
ps = nx.circular_layout(G)  # 布置框架
nx.draw(G, ps, with_labels=False, node_size=30)
plt.savefig('wsnetwork.jpg')
plt.show()

# 绘制度分布图
d = dict(nx.degree(G))
print(d)
print("平均度为：", sum(d.values()) / len(G.nodes))

x = list(range(max(d.values()) + 1))
y = [i / sum(nx.degree_histogram(G)) for i in nx.degree_histogram(G)]
print(x)
print(y)
plt.figure()
plt.bar(x, y, width=0.5, color="blue")
plt.xlabel("$k$")
plt.ylabel("$p_k$")
plt.xlim([6, 15])
plt.savefig('degreeDistribution.jpg')
plt.show()