基于java+MMAS的蚁群算法路由选择可视化动态模拟设计与实现(毕业论文+程序源码)
大家好,今天给大家介绍基于java+MMAS的蚁群算法路由选择可视化动态模拟设计与实现,文章末尾附有本毕业设计的论文和源码下载地址哦。
文章目录:
- 基于java+MMAS的蚁群算法路由选择可视化动态模拟设计与实现(毕业论文+程序源码)
- 1、项目简介
- 2、资源详情
- 3、关键词
- 4、毕设简介
- 5、资源下载
1、项目简介
- 路由选择是一种基于网络层的协议,而所有流行的网络层路由选择协议都是基于以下两种典型的分布式算法之一:距离向量路由算法和链路状态路由算法。组合优化问题是人们在工程技术、科学研究和经济管理等众多领域经常遇到的问题,其中许多问题如旅行商问题、0-1背包问题、图着色问题、装箱问题等,都被证明为NP-困难问题。用确定性的优化算法求NP完全问题的最优解,其计算时间使人难以忍受或因问题的高难度而使其计算时间随问题规模的增加以指数速度延长。用近似算法如启发式算法求解得到的近似解不能保证其可行性和最优性,甚至无法知道所得解同最优解的近似程度。因而在求解大规模组合优化问题时,传统的优化算法就显得无能为力了。在过去的10多年,蚁群算法(ACO)的研究和应用取得了很大的进展,大量结果证明了算法的有效性和在某些领域的优势。蚁群算法是一种新型的模拟进化算法, 研究表明该算法具有并行性, 鲁棒性等优良性质。本文阐述了蚁群算法的原理,详细的说明了蚂蚁算法中各个功能模块,并介绍了该算法在理论和实际问题中的应用, 并对其前景进行了展望。
2、资源详情
项目难度:中等难度
适用场景:相关题目的毕业设计
配套论文字数:17265个字43页
包含内容:整套源码+完整毕业论文
3、关键词
蚁群算法 信息素 仿真4、毕设简介
提示:以下为毕业论文的简略介绍,项目源码及完整毕业论文下载地址见文末。
前言
蚁群算法是一种新生的算法,具有很强的通用性。从提出到现在,仅短短10余年的时间,但是在离散型组合优化问题中。表现很突出,所以一起人们的关注。目前蚁群算法的研究者主要集中在比利时、意大利、德国等国家,美国和日本在近几年也开始了对蚁群算法的研究。国内的研究开始于1998年末。主要在上海、北京、东北少数几个学校和研究所开展了此项工作,主要围绕TSP及相关问题的实验仿真,少数涉及通信网络的路由选择、负载平衡、电力系统的故障检测以及蚁群算法在连续系统应用,如函数逼近等方面应用的尝试。在国外,蚁群算法已经在集成电路布线、网络路由选择、机器人线路规划等方面得到了应用。自1998年,第一届蚂蚁优化国际研讨会召开以来,已经是第三届了,大大推动了蚁群算法的发展。蚁群算法已经引起越来越多的关注,尽管还缺乏完善的理论分析,对它的有效性也没有出严格的数学解释,但是回顾模糊控制的发展历史,理论的不完善并不妨碍应用,有时应用是超前于理论的,并推动理论的研究。我们相信蚁群算法必将得到广泛的应用。
第1章 绪论
1.1 路由选择的意义
路由(Route) 的概念出现于本世纪70 年代,当时的网络结构较简单,因此直至80 年代中期出现了大规模的网络结构后,路由技术才得到了广泛的应用。在ISO/ OSI 体系结构中,路由技术是第三层(网络层) 的功能,路由选择(Routing)是分组交换系统中的一个重要概念,是指在互联网络中选择将信包(Package) 从信源机(Source Host) 传往信宿机(Destination Host) 的传输路径的过程。实际的网络协议(如IP协议) ,其本身并不涉及具体的路由选择细节,它只说明路由选择的一般原理和规则,具体的路由选择是指路由表的建立与刷新机制,由一组独立的路由选择协议(RoutingProtocol) 描述。路由选择的过程是由路由算法来完成的,路由算法可以运行在网络主机上,也可运行在专用的路由设备上,如路由器是一种网络互联设备,其主要功能就是进行路由选择。
1.1.1 路由选择技术的组成
路由选择技术涉及两方面内容:最佳路径的选择及信包在网络上的传递。信包的传递也可称为交换(Switching) , 交换过程相对简单,而路径的选择过程比较复杂。
最佳路径选择
最佳路径依赖于不同的衡量标准,例如可使用路径长度作为衡量标准。在确定最佳路径的路由算法中,路由表(Routing Tables) 是一个重要的数据结构,其中包含了网络的路由信息,算法通过建立和维护路由表进行最佳路径的确定。路由算法根据算法要求在路由表中填写各种路由信息,其中最基本的是目标/ 驿站(Hop) 信息(见表1) 。这一组信息告诉路由器,在信包发往信宿机的过程中,最佳选择是将信息转发至下一驿站(Next Hop) 所代表的节点。当路由器接收到一个输入信息时,首先检查信包的目标地址,然后尝试找出与此目标地址相匹配的下一驿站,若匹配成功则进行信包转发,否则放弃该信包。除了目标/ 驿站信息外,根据不同的路由算法,路由表中还包含有其它内容,例如最佳路径的衡量标准等信息。在路由器之间传输的各种信息中,有关路由选择的信息称为路由刷新报文(Routing Update Message) 。路由刷新报文通常是全部或部分路由表内容。通过对所有路由信息的分析,路由器可建立一个详细的网络拓扑图。例如,用于链接-状态路由算法的链接- 状态广播报文通知其它路由器有关自身的链接状态,通过这些信息,路由器可建立一个完整的网络拓扑图,通过拓扑图便可确定到达目标的最佳路径。
1.1.2 路由算法设计目标
路由算法往往具有下列一种或多种目标: 最佳性、简单性、稳定性、快速收敛性及适应性等目标。
(1) 最佳性目标
要求算法具有寻找最佳路径的能力,最佳路径依赖于算法所采用的衡量标准。通常路由选择协议严格定义了计算时所采用的衡量标准。
(2) 简单性目标
要求算法尽可能简单,即用尽可能小的软件开销提供有效的功能。当算法运行在低档设备上时效率尤为重要。
(3) 稳定性目标
算法必须是稳定可靠的。在遇到特殊情况(如硬件故障、过载、误操作等) 时,算法能够稳定地运行。由于路由器位于互联网络的连接点上, 有着相当重要的地位, 若算法不稳定将造成严重的后果。优秀的路由算法经得起时间的检验并且在任何情况下都能稳定地工作。
(4) 快速收敛性目标
路由算法要求能够快速收敛。这里所指的收敛是指最佳路径能迅速被网上所有路由器所接受。若发生网络故障导致线路断开或恢复, 相应路由器向网络发出路由刷新报文,促使其它路由器重新计算最佳路径,更新路由表,同时又向网络发送刷新报文,直至所有路由器都相互认可这些最佳路径。收敛慢的算法将导致路由环问题及网络损耗。
(5) 适应性目标
路由算法必须具有较强的适应能力,即能够迅速准确地适应各种网络环境的变化。例如,如果发现某一网段出现故障,能迅速为所有经过该网段的路径选择另一条最佳路径。另外,还必须能适应网络带宽、路由器队列大小、网络延迟或其它变化。
1.1.3 路由算法的分类
(1) 静态或动态路由算法
静态路由是由管理员在路由使用前建立的,只有管理员才能对路由表进行修改。静态路由算法的设计简单,在可预知网络的通信量且网络结构简单的情况下使用静态路由算法。静态路由算法不能适应网络情况的变化,因此不适用于目前的大规模及变化频繁的网络结构, 90 年代占主导地位的路由算法是动态路由算法。动态路由算法通过分析路由刷新报文,能够进行实时调整以适应网络的变化。当网络发生变化时,根据路由刷新信息, 路由软件重新计算最佳路径并将变化信息向网络上发送。这些信息在网络上使得网络上的其它路由器也相应运行路由算法刷新其路由表。
(2) 单重路径或多重路径算法
单重路径算法对同一信宿机提供一条最佳路径,多重路径算法对同一信宿机提供多条路径以供选择,允许在复杂的线路上进行多重通信。多重路径算法不仅提高了通信量而且提高了通信的可靠性。
(3) 单层或多层结构算法
单层结构中,网络上所有的路由器是对等的,而在多层结构中,存在主干路由器与分支路由器。信包从分支路由器转发至主干路由器,再传送至信宿机所在区域的主干路由器,再从这一位置通过一个或多个分支路由器最终到达信宿机。
路由系统将一组逻辑节点称为域或自治系统。在层次结构中,有些路由器只能在自治系统内相互通信,位于自治系统顶层的路由器可与其它自治系统的顶层路由器进行通信。层次结构的主要优点在于模仿了公司的组织结构,因为网络的大部分通信量存在于分公司内部(自治系统) ,自治系统内的路由器只需清楚系统内其它路由器的情况。因此系统内的路由算法可进行简化,相应减少了路由刷新时产生的通信量。
(4) 向量- 距离算法或链接- 状态算法
这两种算法是两类基本的自动路径广播算法,在此基础上相应有多种协议,典型的有GGP 和SPF 协议。
1.1.4 路由算法衡量的标准
省略
1.2.目前常用的路由算法
1.2.1 最短路径算法
寻找两顶点间的最短路径的算法很多目前公认最好的算法是Dijkstra在1959 年提出的它不仅求出从始点到终点的最短路径而且最后所得到的实际上是始点到各顶点的最短路径对Dijkstra 算法进行补充得出的步骤如下:
第一步:初始化V={1 2 N} S = {F} D [I ] = L[F I ] Y[ I ] = F 其中I=1,2 ,…N 。F 表示路径的始点I 表示某一顶点N 表示网络中所有顶点的数目V 是所有顶点的集合L[F I]表示从F 点到I 点的距离S 是顶点的集合D 为N 个元素的数组用来存储顶点F 到其它顶点的最短距离Y 为N 个元素的数组用来存储最短路径中在顶点I 之前经过的最近顶点
第二步:从V S 集合中找一个顶点T 使得D[T] 是最小值并将T 加入到S 集合中如果V S 是空集合则结束运算
第三步:调整Y D 数组中的值在V S 集合中对于顶点T 的邻接各顶点I 如果D[I ]> D[T]+L[I T] 那么令Y[I]=T D[I] = D[T]+L[I T]
继续执行第二步
最短路径算法的不足
Dijkstra 算法所采用的数据结构及其实现方法总体上说是比较复杂的其缺点也是明显的难以应付公交线路的网络拓扑中的复杂性主要表现如下:
(1) 数据结构复杂网络在教学和计算领域被抽象为图所以其基础是图的存储表示一般而言无向图可以用邻接矩阵和十字链表表示公交线路网络拓扑很难用现有的数据结构加以完整的表示如果采用现有的最短路径算法分析其建立的公交线路网络图的数据
结构模型将非常复杂
(2) 算法时间长以Dijkstra 算法来计算公交路线最短路径在大数据量的情况下计算速度会慢得让人难以忍受系统设计中要求公交转车的查询必须在较短的时间内完成Dijkstra 算法难以实现
(3) Dijkstra 最短路径算法对于网络拓扑图要求简捷对于复杂的广州公交网络拓扑必须对其进行复杂的抽象合并成简捷的网络拓扑图这无疑增加了程序的复杂性
而蚁群算法是一种新型的模拟进化算法,自从1991 年M. Dorigo 等人首先提出蚁群算法以来,有许多研究人员对该算法进行研究,并成功地应用于解决复杂组合优化问题. 在研究该算法的过程中,研究人员提出一些改进的算法,研究表明该算法具有很好的通用性和鲁棒性,在离散的组合优化问题中实验,取得了良好的效果。下章节就着重介绍一下蚂蚁算法。
第2章 蚁群算法的基本原理
2.1蚂蚁算法的产生
省略
2.2 蚂蚁算法的算法思想
省略
2.3蚁群算法原理
蚁群算法是一种由于受自然界生物的行为启发而产生的“自然”算法。它是从对蚁群行为的研究中产生的。正如M·Dorigo等人在关于蚁群算法的第1 篇文章中指出的:蚁群中的蚂蚁以“外激素”(Stigmergy)为媒介的间接的异步的联系方式是蚁群算法的最大的特点。蚂蚁在行动(寻找食物或者寻找回巢的路径)中,会在它们经过的地方留下一些化学物质(我们称之为“外激素”)。这些物质能被同一蚁群中后来的蚂蚁感受到,并作为一种信号影响后到者的行动(具体表现在后到的蚂蚁选择有这些物质的路径的可能性,比选择没有这些物质的路径的可能性大得多),而后到者留下的外激素会对原有的外激素进行加强,并如此循环下去。这样,经过蚂蚁越多的路径,在后到蚂蚁的选择中被选中的可能性就越大(因为残留的外激素浓度较大的缘故)。由于在一定的时间内,越短的路径会被越多的蚂蚁访问,因而积累的外激素也就越多,在下一个时间内被其他的蚂蚁选中的可能性也就越大。这个过程会一直持续到所有的蚂蚁都走最短的那一条路径为止。(如图)
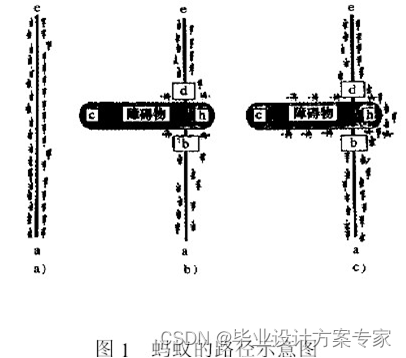
图1中有一条蚂蚁经过的路径,我们假设a点是食物,而e点是蚂蚁的巢穴,如图1 a)所示。在某一个时刻忽然有一个障碍物出现在蚂蚁经过的路径中,原有的路径被切断,从a点到e点的蚂蚁就必须在b点决定应该往左还是往右走。而从a点到e点的蚂蚁也必须在d点决定选择哪条路径。这种决定会受到各条路径上以往蚂蚁留下的外激素浓度(即残留信息浓度)的影响。如果向右的路径上的外激素浓度比较大,那么向右的路径被蚂蚁选中的可能性也就比较大一些。但是对障碍出现后第一个到达b点或d点的蚂蚁而言,因为没有外激素的影响,所以它们选择向左或者向右的可能性是一样的,如图1 b)所示。若以从a点到e点的蚂蚁为例进行说明,对于从e 点到a点的蚂蚁而言过程基本是一样的。由于路径bhd比路径bed要短,因此选择bhd路径的第一只蚂蚁要比选择bed的第一只蚂蚁早到达d点。此时,从d点向b点看,指向路径dhb的外激素浓度要比指向路径deb的外激素浓度大。因此从下一时刻开始,从e点经d点达到a点的蚂蚁选择dhb路径比选择dcb路径的可能性要大得多。从而使路径bhd(或dhb)上外激素浓度与路径bed(或deb)上外激素浓度的差变大。而外激素浓度差变大的结果是选择路径bhd(或dhb)路径的蚂蚁进一步增加,这又导致外激素浓度差进一步加大。
省略
2.4 蚁群算法的应用
2.4.1蚂蚁算法在电信网动态路由优化中的应用
针对我国电信网的具体情况,提出借助蚂蚁算法,用分散控制的方式实现电信网动态路由优化的一种方案,目的是提高网络资源的利用率、网络运行的效率和可靠性。
2.4.2蚂蚁算法在组合优化中的应用
蚂蚁算法是近年来新出现的一种随机型搜索寻优算法 ,自从在 TSP等著名问题中得到富有成效的应用之后 ,已引起越来越多的关注和重视 .本文进一步将这种新型的生物优化思想扩展到其他一些组合优化难题 ,包括目前尚缺乏有效求解手段的多目标组合优化问题 ,从实验上探索了蚂蚁算法的优化能力 ,获得了满意的效果。
2.5 蚂蚁算法的未来发展
自从1991 年M. Dorigo 等人首先提出蚁群算法以来,有许多研究人员对该算法进行研究,并成功地应用于解决复杂组合优化问题. 在研究该算法的过程中,研究人员提出一些改进的算法。
2.5.1 MMAS ( Max2Min ant system) 最大最小蚁群算法
其基本思想是:只让最佳路径的外激素增加,加快收敛速度;为了避免算法过早收敛于非全局最优解,将各条路径可能的外激素浓度限于[τmin ,τmax ] ,超出这个范围的值被强制设为τmin 或τmax ,可以有效地避免某条路径上的信息量远大于其余路径,使蚂蚁都集中到同一条路径上,这样使算法不再扩散;将各条路径上外激素的起始浓度设为τmax ,这样便可以更加充分地进行寻优。
2.5.2 具有变异特征的蚁群算法
当群体的规模较大时,需要较长时间才能搜索到最佳路径. 为了克服此缺点,受遗传算法中的变异算子的启发,提出具有变异特征的蚁群算法. 算法中使用逆转变异方式, 即设某个体走的路径是:i0i1i2 ⋯i (n- 1) , (i0 ,i1 , ⋯i (n- 1) ∈{0 ,1 ,2 , ⋯,n - 1})如果满足 其中s1 ,s2 ∈{0 ,1 , ⋯, (n - 1) } , %表示整除. 将s1 + 1 和s2这一段颠倒过来. 此算法引入变异算子,经较少的进化代数就可以找到较好的解。
2.5.3 自适应蚁群算法
在此算法中采用确定性选择和随机选择相结合的选择策略,并在搜索过程中动态调整确定性选择的概率. 当进化到一定代数后,进化方向已经基本确定,对路径上的信息量进行动态调整,缩小最好和最差路径上的信息量的差距,并适当加大随机选择的概率,以利于对空间的完全搜索,可有效地克服基本蚁群算法进化速度慢及易陷入局部最优解的缺陷。
2.5.4大规模集成电路综合布线
大规模集成电路中的综合布线可以采用蚁群算法的思想来进行(在布线过程中,各个引脚对蚂蚁的引力可根据引力函数来计算。各个线网Agent根据启发策略,象蚁群一样在开关盒网格上爬行,所经之处便布上一条金属线,历经一个线网的所有引脚之后,线网便布通了。给定一个开关盒布线问题,问题的计算量是固定不变的。主要由算法的迭代次数决定,而迭代次数由Agent的智能和开关盒问题本身的性质确定蚁群算法本身的并行法,使之比较适合于解决布线问题。
2.5.5电信网络路由
电信网络中的路由是通过路由表进行的。在每个节点的路由表中!对每个目的节点都列出了与该节点相连的节点,当有数据包到达时,通过查询路由表可知道下一个将要到达的节点,首先对路由表中的信息素强度进行初始化。在节点Xi以节点i为目的地址,邻节点为J处的信息素强度为从X经节点J到节点i路径的最小费用值。然后周期性地释放蚂蚁来进行路由。并修改相应的信息素的值。无论呼叫是均匀分布还是集分布,利用蚁群算法所得呼叫拒绝率和平均路径长度均小于最小负载法结果:在呼叫符合集中分布时,蚁群算法所得呼叫拒绝率低于最短路径法。
第3章 开发工具
3.1软件环境
装有JDK的JAVA环境的计算机,由于蚂蚁算法演示是用JAVA做的一个小程序,所以在装有JAVA环境的机子上都能够运行。
3.2其他资料
JAVA工具书,软件工程工具书。面向对象工具书。
3.3 Java 的简单介绍
3.3.1 网络时代的需要
省略
3.3.2 Internet的普及
省略
3.3.3 跨平台可移植性的要求
省略
3.4 Java 的主要特点
省略
第4章 具体的功能结构
4.1 系统的结构总框图
、
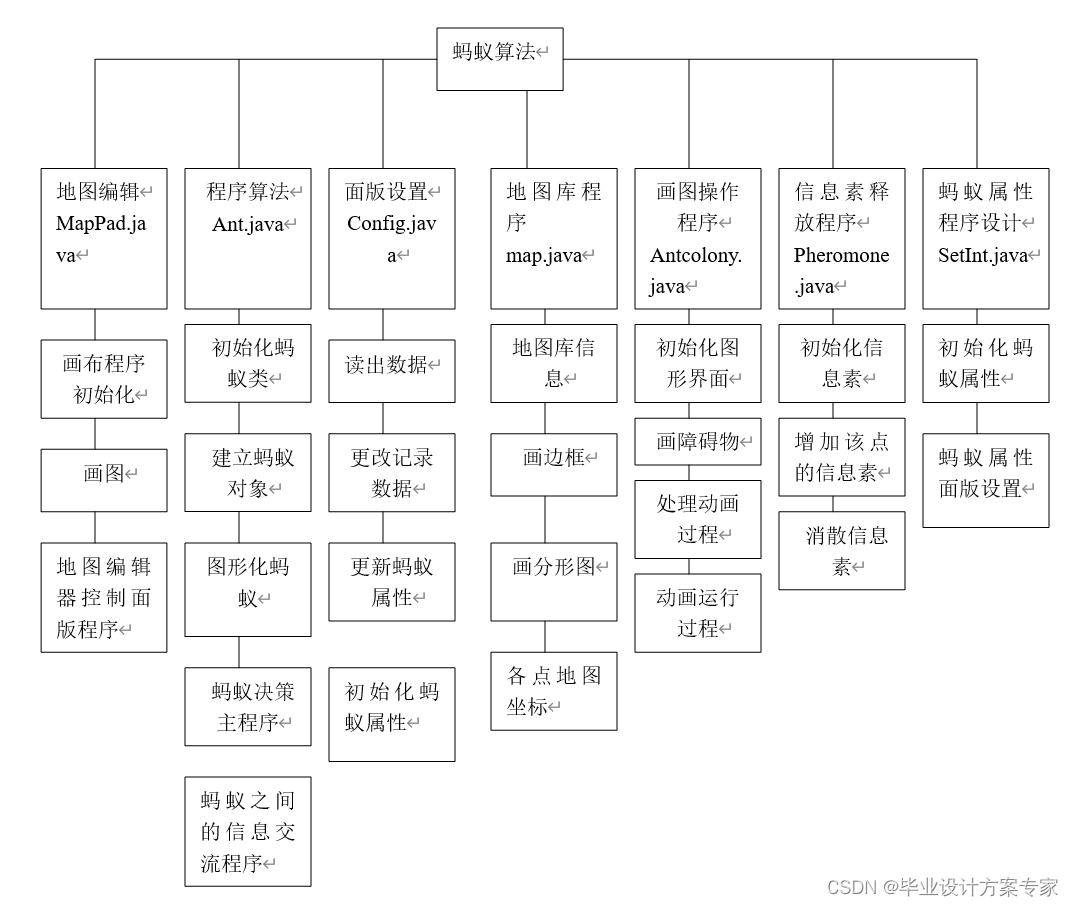
4.2 蚂蚁算法的主要步骤
第一步:判断蚂蚁是否已经找到目标点(在蚂蚁没有找到食物之前,目标点是事物,找到食物后,目标点则换成蚂蚁的窝);
实现代码:
if(Judged==false){
if(JudgeEnd()){
//判断目前蚂蚁是否已经到了目标点,,如果找到了目标点那么就退出该程序
Judged=true;
return;
}
}
第二步:计算蚂蚁的主方向,也就是让蚂蚁的爬动有一个惯性,当没有信息素做指导的时候蚂蚁就按照主方向运动;
实现代码:
private double SelectDirect(){
//选择方向,最后选择的方向为主方向加一个随机扰动
double direct,e=0;
if(Main_direct<0){
//如果目前还没有主方向角,就随机的选择一个
e=2*Math.PI*Math.random();
Main_direct=e;
}
//选择主方向角
direct=Main_direct;
//做一个随机模型,产生两个随机数,x,y都是[0,1]内的,这样x^2-y^2就是一个 [-1,1]的随机数,并且在0点附近的概率大,两边小
double re=Math.random();
double re1=Math.random();
direct+=Math.PI*(re*re-re1*re1)/2;
if(re<0.02){
//以小一定的概率0.02改变主方向的值,主方向的选取为从蚂蚁记住的点中随机选一个点,计算当前点和这个点之间的方向角。
int size=(int)(re1*memory)+1;
if(HistoryPoint.size()>size){
Point pt=(Point)(HistoryPoint.elementAt(HistoryPoint.size()-size));
if(pt.x!=nowPt.x||pt.y!=nowPt.y){
Main_direct=GetDirection(pt,nowPt);
}
}
}
return direct;
第三步:开始搜索自己周围的空间信息,包括有多少信息素,是否有障碍物;
实现代码:
//开始搜索环境,搜索的空间是以当前点为中心,VR为半径的四方形内,即VR/2*VR/2的正方形
for(int x=-VR;x<=VR;x++){
for(int y=-VR;y<=VR;y++)
{
if(x!=0||y!=0){
if(maxphe<phe){
//如果当前点的信息素是0,则表示蚂蚁还在窝里,如果是1,就要根据随机数
//以mistake来决定蚂蚁犯错误的概率,即如果犯错误,它就不按信息素最大的方向走
double ra=Math.random();
if(here==0||ra>mistake){
boolean found=false;
//查一下内存最近走过的的点数,从而避免当地转圈
int size=HistoryPoint.size();
int minsize=memory;
if(size<memory)minsize=size;
for(int i=size-1;i>=size-minsize;i--){
Point pt=(Point)(HistoryPoint.elementAt(i));
if(pt.x==xx&&pt.y==yy){
found=true;
break;
}
}
if(!found){
//如果没有原地转圈,那么记录信息素。
maxphe=local_colony.Pheromone_grid[1-kind][xx][yy];
deltx=x;
delty=y;
}
}//end here==0||ra>0.001
}//end maxphe<here
}//end if x!=0
}//end for y
}//end for x
Point pt;
第四步:根据信息素的大小决定蚂蚁的移动方向;
实现代码:
//根据获得的信息的来的位移量deltx,delty,来具体的进行移位
pt=Evade_obs(deltx,delty);
第五步:根据决策的目标进行移动,其中包括遇见障碍的躲避和洒下自己的信息素。
(1)躲避障碍物
如果遇到障碍物,就根据主方向来确定位移,如果主方向也有障碍物了,那蚂蚁就会随机变换自己的主方向。
实现代码:
if(pt.x==nowPt.x&&pt.y==nowPt.y){
pt=Evade_obs(deltx1,delty1);
}
(2)洒下自己的信息素
在本程序中,蚂蚁洒下信息素的功能是通过一个子程序实现的,
实现代码:
if(Pheromone_count<=0)return;
//决定释放信息素的种类
int kind=FoundTimes%2;
//获得当前点环境已有信息素的值
int Phec=local_colony.Pheromone_grid[kind][lastPt.x][lastPt.y];
boolean ofound=false;
if(Phec!=0){
//如果当前点已经有信息素了在信息素向量中查找该点的信息
for(int i=0;i<local_colony.phe.size();i++){
Pheromone ph=(Pheromone)(local_colony.phe.elementAt(i));
if(lastPt.x==ph.x&&lastPt.y==ph.y&&ph.kind==kind){
//找到了,则看看蚂蚁所在的位置是否是刚刚走过的,如果不是才撒信息素
int size=HistoryPoint.size();
//如果在表中找到信息素,则用ofound记录。
ofound=true;
boolean found=false;
if(size>4){
for(int j=size-4;j<size-1;j++){
Point pt=(Point)(HistoryPoint.elementAt(j));
if(pt.x==lastPt.x&&pt.y==lastPt.y){
//如果当前点重复了以前走过的路,就不释放
found=true;
break;
}
}
}
if(!found){
//如果当前点不重复,则开始撒
ph.Add(Phe);
local_colony.Pheromone_grid[kind][lastPt.x][lastPt.y]+=Phe;
//让还剩下的信息素总量减少
Pheromone_count-=Phe;
}
break;
}
}
}
if(Phec==0||!ofound){
//如果当前环境没有信息素,或者当前环境的信息素来自窝或者食物,则新建一个信息素元素放到列表中
Pheromone ph=new Pheromone(lastPt.x,lastPt.y,local_colony.phe.size(),local_colony.Delimiter,id,local_colony,Phec,kind);
ph.Add(Phe);
local_colony.Pheromone_grid[kind][lastPt.x][lastPt.y]+=Phe;
local_colony.phe.addElement(ph);
//让还剩下的信息素总量减少
Pheromone_count-=Phe;
}
//根据还剩下信息素的量调整释放信息素的数值Phe, //把剩余信息量看成数组count(n),count(n)以几何级数的速度递减,这样,蚂蚁刚走出的地方信息素远远高于后走的地方
Phe=(int)(0.005*Pheromone_count);
//如果剩余信息素已经太小了,则按照等差数列递减
if(Phe<=10)Phe=10;
}
第5章 系统的实现
5.1蚁群算法的实现结果
程序执行后的到的结果如图:
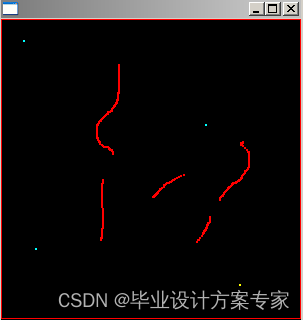
程序运行说明:
浅蓝色的点表示食物,黄色的点表示窝,雾状的点表示蚂蚁留下的信息素,红色的点表示障碍物,白色的动点就是蚂蚁了(此图中还没有开始执行,所以暂时没有白色的点)。按设置按钮你可以更改一些环境变量,也可以更改单个蚂蚁的属性。在设置参数窗口中显示了整个蚂蚁群中找到的从它的窝到食物的最短路径。
预期的结果:
各个蚂蚁在没有事先告诉他们食物在什么地方的前提下开始寻找食物。当一只找到食物以后,它会向环境释放一种信息素,吸引其他的蚂蚁过来,这样越来越多的蚂蚁会找到食物!有些蚂蚁并没有象其它蚂蚁一样总重复同样的路,他们会另辟蹊径,如果令开辟的道路比原来的其他道路更短,那么,渐渐,更多的蚂蚁被吸引到这条较短的路上来。最后,经过一段时间运行,可能会出现一条最短的路径被大多数蚂蚁重复着。
下面是程序运行的连续截图:

上图是刚开是执行时,白色的蚂蚁从黄色的窝中出来,是按随机的方向出发,所以看上去基本上是个圆。

上图中是一只蚂蚁找到了左下角的事物,随即将窝作为目标点,向窝移动,并在一边向窝移动的过程中一边留下信息素(蓝色的轨迹),其他的蚂蚁仍在寻路中。
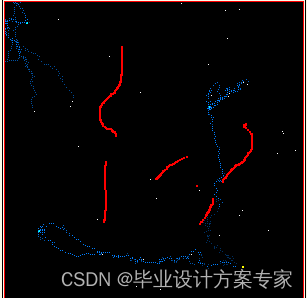
从上图中我们可以看到,其他蚂蚁找到了食物,在回窝的过程中,它根据以前的蚂蚁留下的信息素找到了路径。
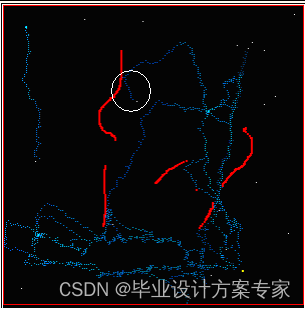
看上图,一只蚂蚁在找到事物回窝的过程中,遇到了障碍(图中圆圈标记处),此时周围也没有其他的信息素,所以就根据主方向来确定位移,如果主方向也有障碍物了,那蚂蚁就会随机变换自己的主方向。

在此图中我们追踪刚才遇见障碍的那只蚂蚁(图中圆圈标记处),由于在它在移动过程中又遇到了其他蚂蚁留下的信息素,所以它后面的路径就会沿着以前的蚂蚁的路径。
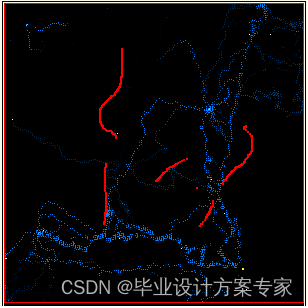
上图是在程序执行了比较长一段时间后的截图,由图中我们可以看出越来越多的蚂蚁集中到一条比较短的路径上,在这条路径上留下的信息素也比较多,其他的路径由于不是最优解,走过的蚂蚁比较少,留下的信息素也就比较少,信息素的保留有一定的时间的,如此循环最终该路径就没有蚂蚁路过,该路径就淘汰。
第6章 算法的不足和改进
6.1 算法的不足
虽然蚁群算法已经被证明是一种有效的解决组合优化问题的方法,但是由于问世的时间比较短,还存在如下不足:
- 限于局部最友解。从算法的性质而言,蚁群算法也是在寻找一个比较好的局部最优解,而不是强求是全局最优解。
- 工作过程的中间停滞问题。和算法开始时收敛速度一样,在算法工作过程当中,迭代到一定次数后,蚂蚁也可能在某个或些局部最优解邻域附近发生停滞。
- 较长的搜索时间。尽管和其他算法相比,蚁群算法在迭代次数和解的质量上都有一定的优势,但是对于目前计算机网络的实际情况,还是需要较长的搜索时间。虽然计算机计算速度的提高和蚁群算法的并行性在一定程度上可以缓解这一问题,但是对于大规模复杂的计算机网络,这还是一个很大的障碍。
4 蚂蚁的数量影响算法的性能
实验前提: 其他的参数值都不变
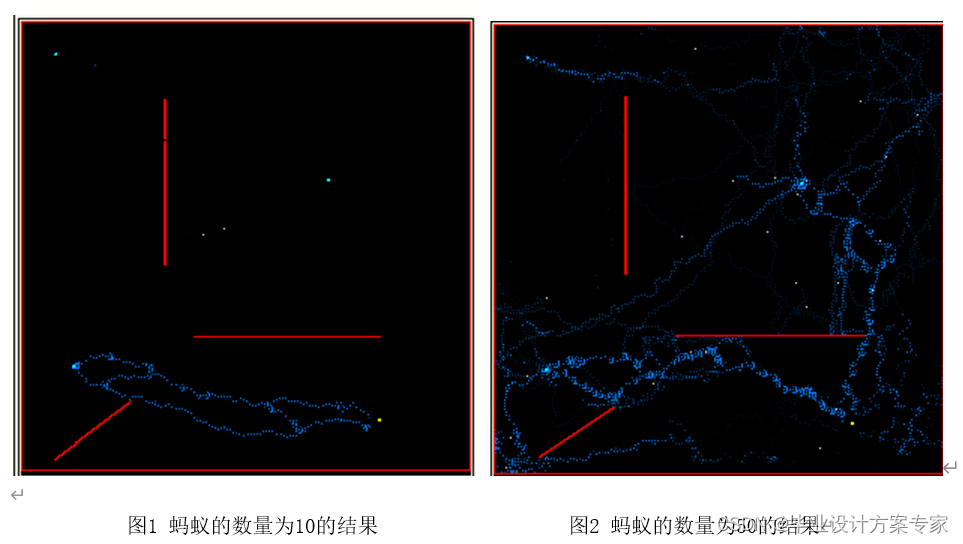
由实验结果可知,算法的性能随着蚁群数量的增加有很大提高,但是运行时间也延长了不少。所以,选择蚁群数量取决于应用场合对算法的要求。蚁群算法存在很多有待改进的地方。文中只是对通过实验发现的不稳定因素做了简要的分析,因为实验是有偶然性的,所以发现的问题和对问题的分析只是一种探讨性的研究。蚁群算法中如何调整信息素将是一个难题,同时也是以后研究的重点。
6.2 算法的改进
6.2.1信息素更新参数微调
省略
6.2.2 全局调整
省略
6.2.3 信息素值微调
省略
6.3一种先进的蚂蚁算法——智能蚂蚁算法
省略
6.4 蚂蚁算法的展望
蚁群算法具有广阔的研究空间,已经引起众多研究者的广泛兴趣和关注,通过每2年一届的ANTS国际学术会议可见一斑。从1998年开始至今,在比利时的布鲁塞尔已经举行了3届ANTS国际学术会议。目前在理论方面,研究者们正在努力扩展有理论成果的范围,确定一个完整的理论框架,例如在确定算法的参数值、证明算法的收敛性等方面进行研究;在实践方面,大多数研究着重于扩展算法所能解决问题的范围,从而解决连续优化、动态优化等一些现实问题。它是一种新型的模拟进化算法,虽研究时间不长,已显示出求解复杂优化问题方面的优势!其应用前景非常广泛:例如交通网络中的最佳路径选择问题,电信网络中的流量负载分配问题等等都可以应用该算法来解决,但是蚁群算法还不像其它的启发式算法那样已形成系统的分析方法和具有坚实的数学基础,参数的选择更多的是依靠实验和经验,没有定理来确定,而且它的计算时间偏长,这些都表明其在理论和实践方面尚有许多问题需要更深入的研究与解决。但是它具有正反馈、并行计算和强鲁棒性等优点,从当前的研究和应用情况来看,它具有强大的生命力,可以预见其发展的前景是十分光明的。
结束语
本文简单介绍了“蚂蚁算法”,模拟进化算法的思想来源于对现实世界的挖掘、归纳和总结,蚁群算法也不例外。蚁群的活动中信息素起这关键的作用。信息素可以理解为个体之间的相互影响的一个正反馈机制,信息素越多的路径吸引的蚂蚁就越多,最终实现最优路径的选择。这就是蚁群算法的基本原理。
蚁群算法作为一种新的模拟进化算法,虽然尚未有严格的理论基础,但是它具有正反馈、并行计算等优点,从当前的研究和应用情况来看,它具有强大的生命力,可以预见其发展前景是十分光明的。
致谢
省略
参考文献
[1] Dorigo M,Gambardella L M.Ant colony system: A cooperative learning approach to the traveling salesman problem,IEEE Trans. Evolutionary Computation,1997,1(1):53-66.
[2]“Flocking and Collective Movement”,
http://leanair4.mit.edu/docushare/dscgi/ds.py/Get/File-376/OH_EE141_W2flocking.pdf
[3]李夏,戴汝为,“系统科学与复杂性”,自动化学报,第24卷第4期,1998/7
[4] 樊玮,朱军,“软件Agent技术的研究”, 航空计算技术,第29卷第4期,1999/12
[5]K. Sugawara et al., “Foraging Behavior of Multi-robot System and Emergence of Swarm Intelligence”, Systems, Man, and Cybernetics, 1999. IEEE SMC’99 Conference Proceedings. 1999 IEEE International Conference on, Volume:3, 1999 Page(s):257-262 vol 3
[6]Bill Fulkerson, Van Parunak,“The Living Factory: Applications of Artificial Life to Manufacturing”,IEEE 1995
5、资源下载
本项目源码及完整论文如下,有需要的朋友可以点击进行下载。如果链接失效可点击下方卡片扫码自助下载。
| 序号 | 毕业设计全套资源(点击下载) |
|---|---|
| 本项目源码 | 基于java+MMAS的蚁群算法路由选择可视化动态模拟设计与实现 |



![[附源码]java毕业设计流浪宠物免费领养系统](https://img-blog.csdnimg.cn/8d7f4a5f21c34927a95b0493402c8437.png)









![Spring七天速成[精简版]:入门必看(一)收藏起来](https://img-blog.csdnimg.cn/75f85f447d8745f2b86a3daa761ebf85.png)