目录
3.4 tensor中的填充操作
3.4.1 tensor.full
3.5 pytorch中模型的保存/加载/并行化
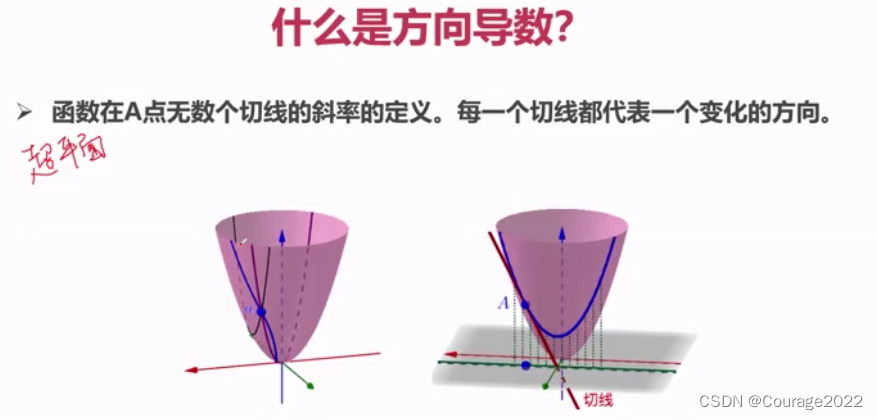
3.6 导数、方向导数、偏导数
3.6.1 重要概念
3.6.1.1 概念
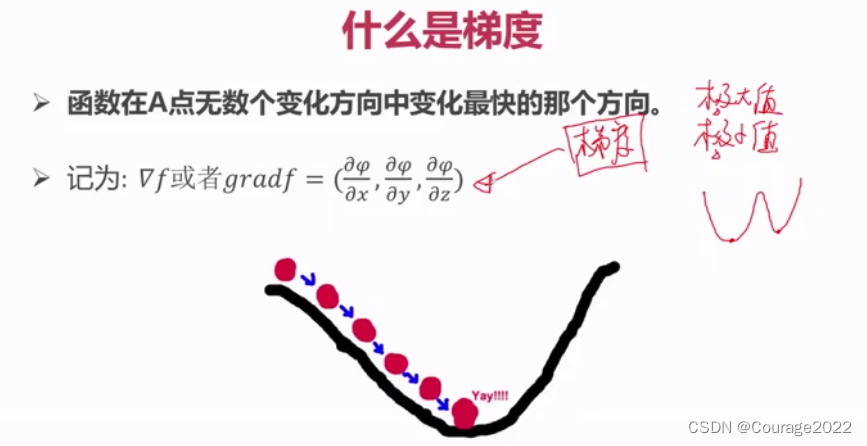
3.6.1 如何计算梯度
3.6.2 torch.autograd.Function
3.7 pytorch与nn库
3.7.1 nn库介绍(介绍、在后续会详细讲解)
3.7 Visdom介绍
3.8 tensorboardX
3.4 tensor中的填充操作
3.4.1 tensor.full
定义tensor,并填充指定数值。
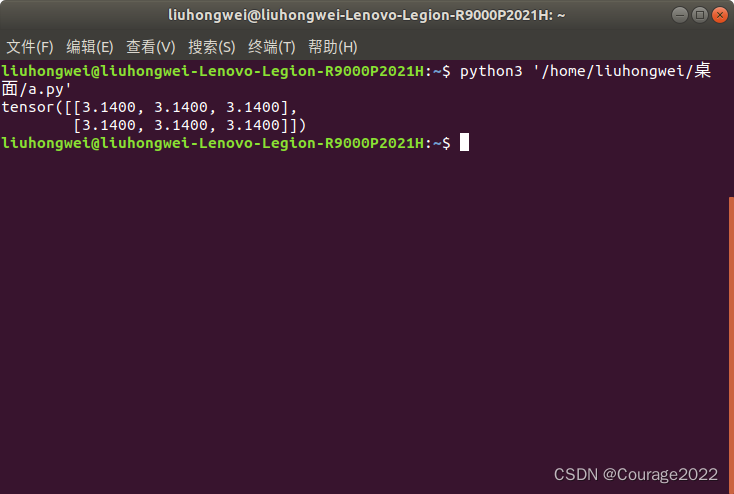
import torch a = torch.full((2,3),3.14) print(a)
3.5 pytorch中模型的保存/加载/并行化
3.6 导数、方向导数、偏导数
在pytorch中我们定义requires_grad设置属性来设置是否计算梯度。
3.6.1 重要概念
3.6.1.1 概念
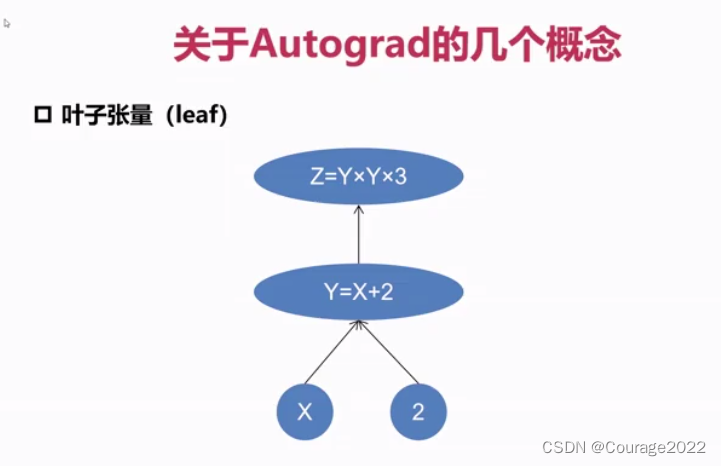
称之为叶子张量,我们想要计算一个张量的梯度,必须满足当前的节点属于叶子节点。只有是一个叶子张量我们才能计算它的梯度,因此只有
是有梯度值的!
通过调用backward函数可以实现对叶子节点自动梯度的求解
3.6.1 如何计算梯度
import torch from torch.autograd import Variable # part 1 #x = Variable(torch.ones(2, 2), # requires_grad=True) x = torch.ones(2, 2, requires_grad=True) x.register_hook(lambda grad:grad*2) y = x + 2 z = y * y * 3 # z = torch.sum(z) # nn = torch.rand(2, 2) nn = torch.ones(2, 2) print(nn) z.backward(gradient=nn, retain_graph=True) torch.autograd.backward(z, grad_tensors=nn, retain_graph=True) print(torch.autograd.grad(z, [x, y, z], grad_outputs=nn)) print(x.grad) print(y.grad) print(x.grad_fn) print(y.grad_fn) print(z.grad_fn)
3.6.2 torch.autograd.Function
import torch class line(torch.autograd.Function): @staticmethod def forward(ctx, w, x, b): #y = w*x +b ctx.save_for_backward(w, x, b) return w * x + b @staticmethod def backward(ctx, grad_out): w, x, b = ctx.saved_tensors grad_w = grad_out * x grad_x = grad_out * w grad_b = grad_out return grad_w, grad_x, grad_b w = torch.rand(2, 2, requires_grad=True) x = torch.rand(2, 2, requires_grad=True) b = torch.rand(2, 2, requires_grad=True) out = line.apply(w, x, b) out.backward(torch.ones(2, 2)) print(w, x, b) print(w.grad, x.grad, b.grad)
3.7 pytorch与nn库
3.7.1 nn库介绍(介绍、在后续会详细讲解)
1.nn.Parameter:
我们设计一个神经网络时需要构造一个模型:包括结构和参数,结构即设计的网络结构,比如网络由几层每一层如何卷积每一层的通道有多少等等。参数就是待训练的参数,通过迭代优化求解。
我们用nn.Parameter定义可训练的参数,也可以通过self.register_parameter注册可训练参数,我们也可以定义字典和列表的参数。
2.nn.Linear:
3.nn.functional
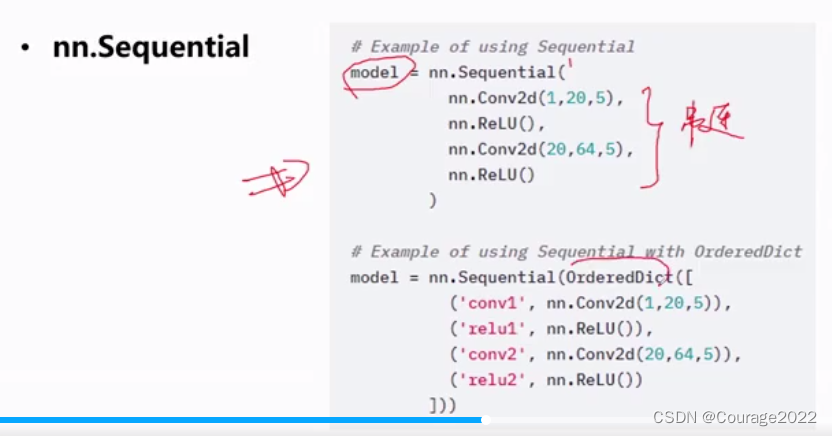
4.nn.Sequntial
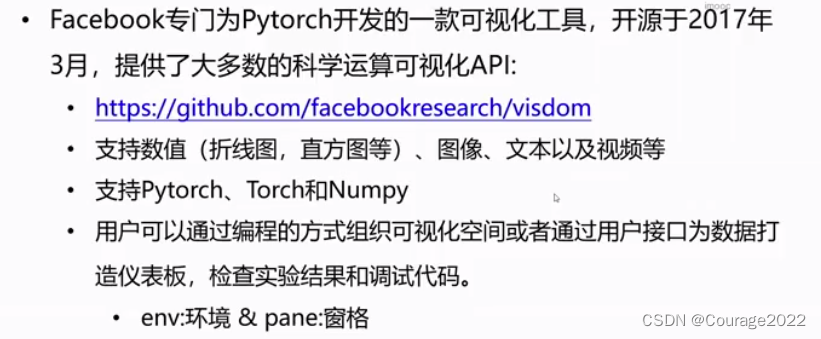
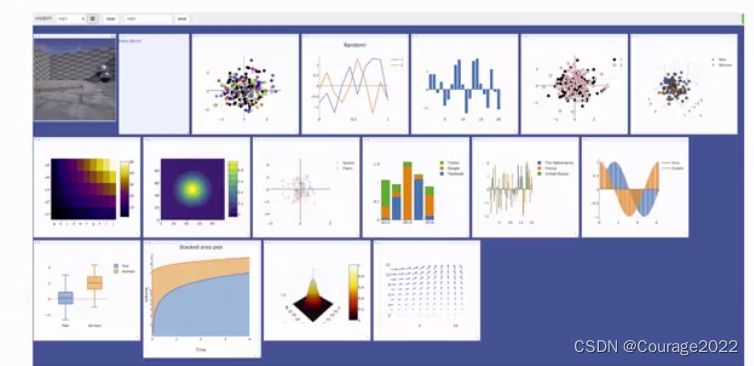
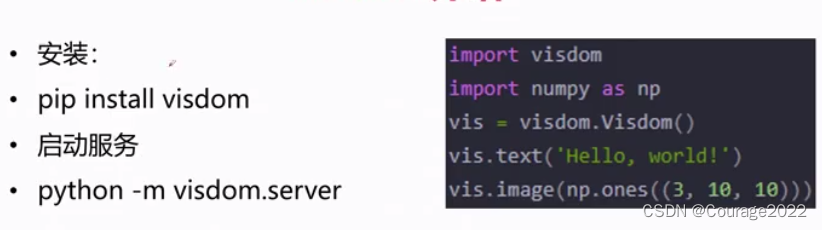
3.7 Visdom介绍
3.8 tensorboardX
也是一种图像可视化工具:




















![[附源码]java毕业设计流浪宠物免费领养系统](https://img-blog.csdnimg.cn/8d7f4a5f21c34927a95b0493402c8437.png)









![Spring七天速成[精简版]:入门必看(一)收藏起来](https://img-blog.csdnimg.cn/75f85f447d8745f2b86a3daa761ebf85.png)