文章目录
- 线性回归和逻辑回归
- StandardScaler处理
- 线性分类
- 乳腺癌数据集breastCancer
- 鸢尾花数据集iris
线性回归和逻辑回归
线性回归就是预测一个连续变量的值,线性回归假设因变量和自变量之间是线性关系的,线性回归要求因变量是连续性数值变量训练数据的特征作为自变量,训练数据所属于的类别作为因变量,假设在因变量和自变量之间存在线性函数关系式,通过大量的训练样本对模型进行训练,然后不断调整函数关系式中的权重也就是参数值,使得到的这个函数关系式能够针对每个训练样本给出符合预期的结果。在这个训练参数的过程中依据的是平方差也就是预测值和实际值之间的平方差作为cost函数,要使参数的值满足cost函数的值最小,通过不断的减少cost的值来不断的优化参数的值。这里求出的函数模型是一个连续函数,在二维空间中可以使用一条直线来表示,当数据的特征值增大的时候会是相应维数空间上的一个线性超平面。
逻辑回归一般用于分类,用来表示某件事情发生的可能性,因为它的输出值在[0, 1]之间可以看出是一种概率。在这里以二分类为例说明,假设因变量和自变量之间的关系是非线性,一般的输出的值在[0, 1]之间,也就是两个类别,一个是0,一个是1,在x<0的时候使y=0,当x=0时,y=0.5,当x>0的时候,y=1,但是这样的函数关系式不连续,所以使用sigmoid函数进行拟合,这样使因变量和自变量之间的函数关系式为非线性的并可以限制输出在[0, 1]之间。逻辑回归可以看成是在线性回归的基础上加了一个 Sigmoid 函数,逻辑回归使用对数函数作为cost函数。
线性回归一般解决回归问题,也就是预测连续的、具体的数值。应用在一些数据的拟合,用于预测一些值,将其按照之前训练好的模型预测出未出现的值。
StandardScaler处理
对数据集进行StandardScaler处理和MinMaxScaler处理有所区别
StandardScaler主要是用来去均值和方差归一化的,通过pycharm中查看源码显示Standardize features by removing the mean and scaling to unit variance。这个函数使用的计算方法为z = (x - u) / s,u is the mean of the training samples or zero if with_mean=False,and s is the standard deviation of the training samples or one if with_std=False.通过这个操作可以让数据都在0附近,方差为1,这样使数据更加集中更加聚集,还可以用训练集的参数也就是训练集的方差和均值来标准化测试集,将样本的特征值转换到同一量纲下,常用与基于正态分布的算法,比如回归。
MinMaxScaler主要是用来标准化数据集的特征到一个指定的范围,默认是[0, 1],通过pycharm中查看源码显示Transform features by scaling each feature to a given range.这个函数使用的计算方法为X_std = (X - X.min(axis=0)) / (X.max(axis=0) - X.min(axis=0))。这种方法是对原始数据的线性变换,一般是将数据归一到[0,1],这种方法只适用于数据在一个范围内分布的情况,可以提升模型收敛速度,提升模型精度,常见用于神经网络。
# # 使用StandrdScaler预处理数据集,使其离差标准化
scaler = StandardScaler()
scaler.fit(X_train)
X_train_scaler = scaler.transform(X_train)
X_test_scaler = scaler.transform(X_test)
# # 使用MinMaxScaler预处理数据集,使其离差标准化
# scaler = MinMaxScaler().fit(X_train)
# X_train_scaler = scaler.transform(X_train)
# X_test_scaler = scaler.transform(X_test)
线性分类
代码分别使用了LogisticRegression和SGDClassifier两种分类方法(SGD,随机梯度下降,Stochastic Gradient Descent)
# 使用LogisticRegreeion分类器学习和测试
lr = LogisticRegression()
lr.fit(X_train_scaler, y_train)
y_pred_lr = lr.predict(X_test_scaler)
# 使用SGDClassifier分类器学习和测试
sgd = SGDClassifier()
sgd.fit(X_train_scaler, y_train)
y_pred_sgd = sgd.predict(X_test_scaler)
每次运行代码,线性分界面位置和分类准确率都不同,针对LogisticRegression创建的逻辑回归分类器,它使用的训练样本和测试样本是在之前使用train_test_split函数进行分类的,,其中有个random_state参数,相当于一个随机数种子,如果将这个参数设置为一个整数后就可以保证训练集和测试集的可重见性,所以在这个函数的参数设置之后,LogisticRegression分类器的准确率就会保持不变,但是SGDClassifier分类器的准确率还是会变化,因为SGDClassifier是随机梯度下降法分类器,每次迭代都随机从训练集中抽取出1个样本,所以可能就会在不是用到全部的训练数据就使cost函数的值在可接受范围之内,所以每次的准确率不一样。
并不代表分类器的性能是不稳定的,因为这个准确率可以保证在一定的范围内,可以有效的预防过拟合的现象发生。
可以使用模型的平均准确率来评判模型的性能,因为模型可能会受噪声点的影响,因为数据集在分割的时候如果噪声点的分类可能会造成过拟合或者是会造成模型判断的准确性降低。
乳腺癌数据集breastCancer
截取程序中准确率较高的结果如下,使用20和29维特征:
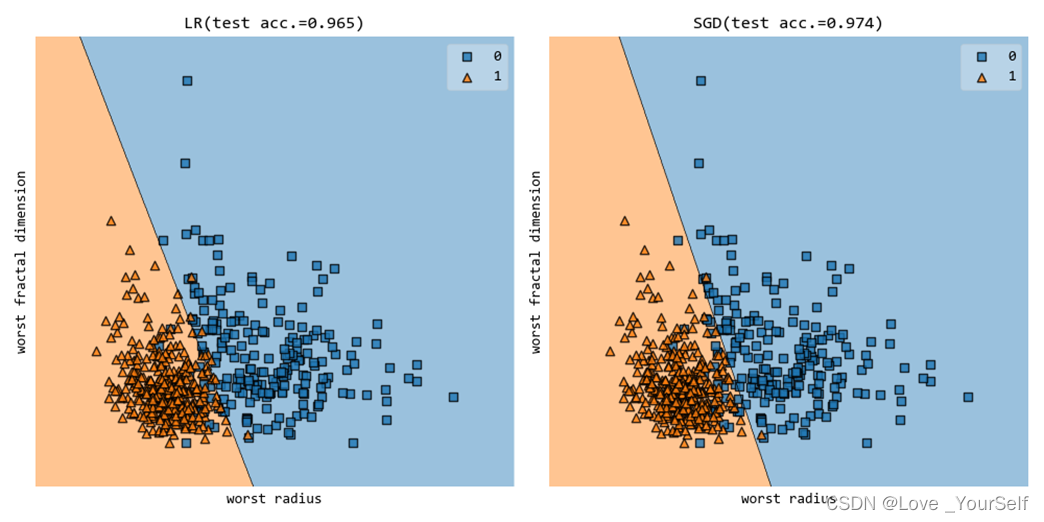
当使用第20和第25维特征的时候的分类准确率
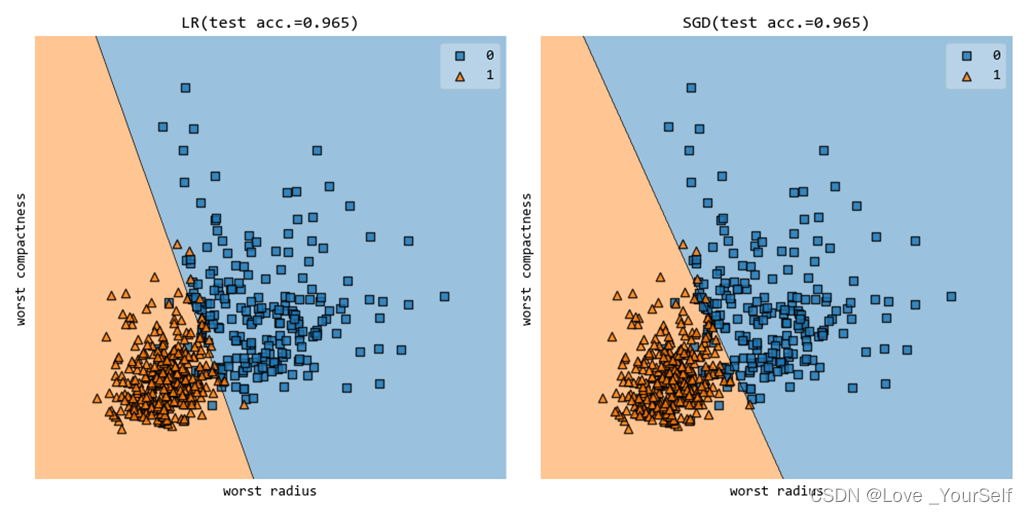
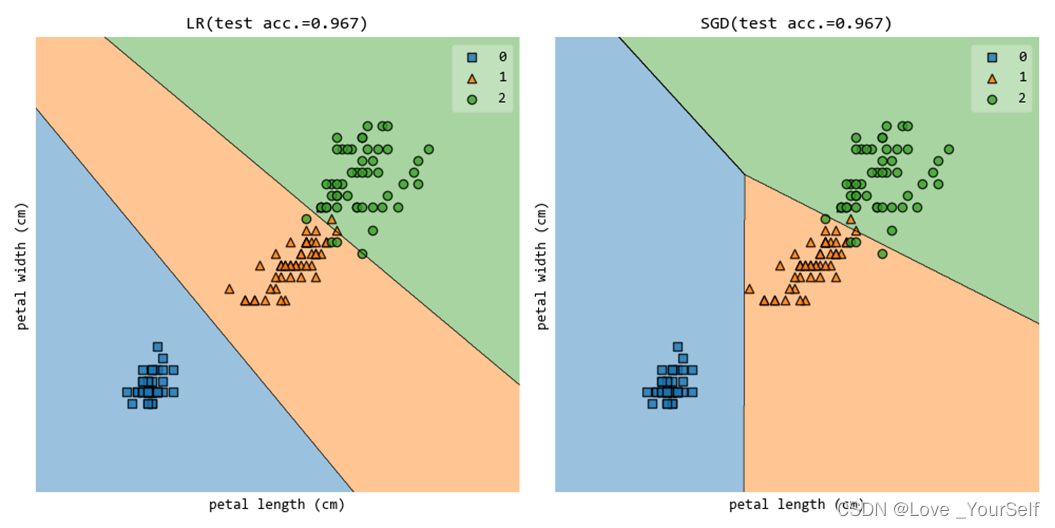
鸢尾花数据集iris
使用第0维(‘sepal length (cm)’)和第2维(‘petal length (cm)’)特征的时候结果如下:
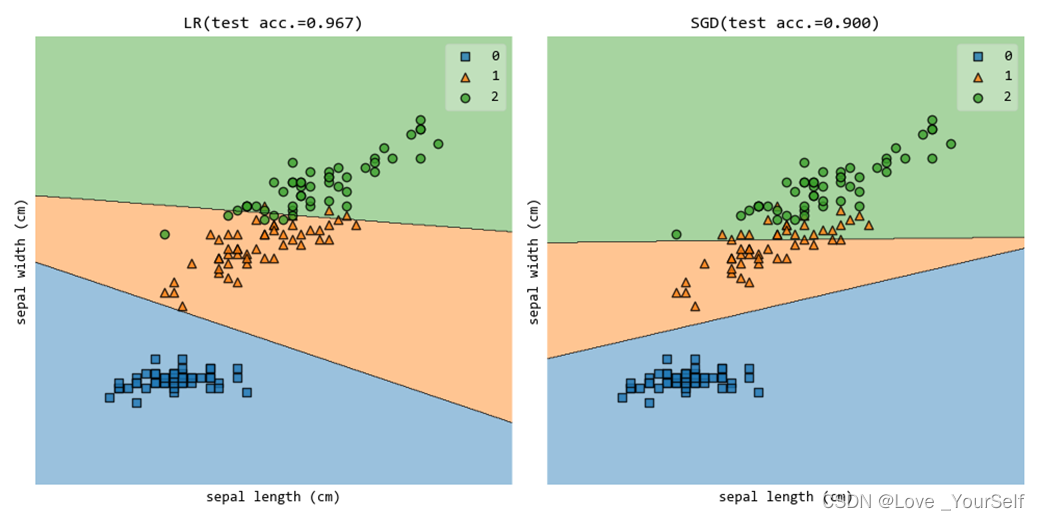
使用第0维(‘sepal length (cm)’)和第1维(‘sepal width (cm)’)特征的时候结果如下:
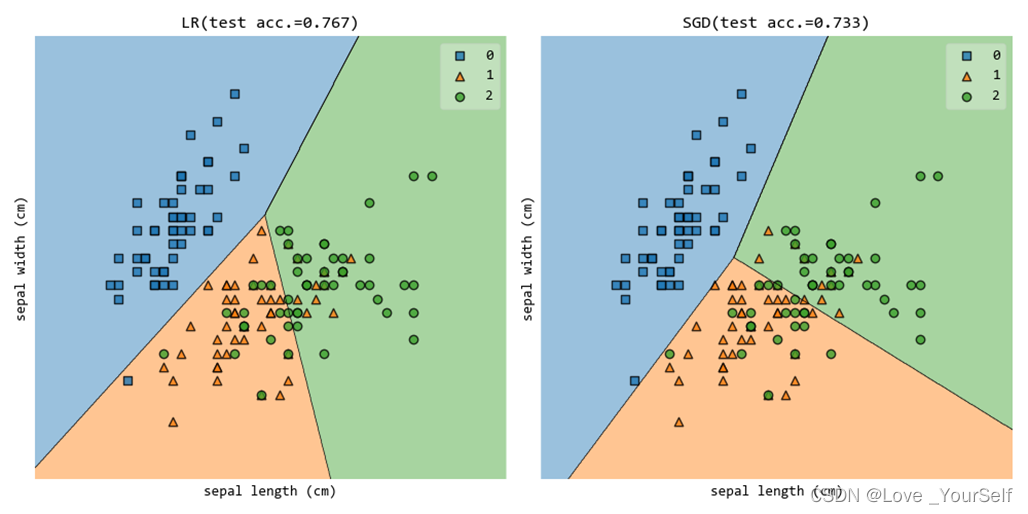
使用第1维(’ sepal width (cm)')和第2维(‘petal length (cm)’)特征的时候结果如下:
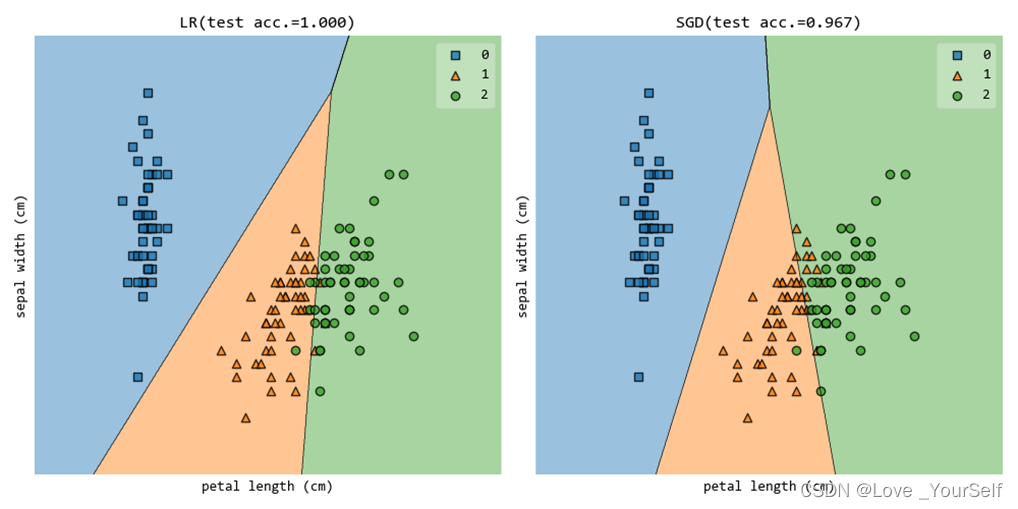
使用第2维(‘petal length (cm)’)和第3维(petal width (cm))特征的时候结果如下:








![Spring七天速成[精简版]:入门必看(一)收藏起来](https://img-blog.csdnimg.cn/75f85f447d8745f2b86a3daa761ebf85.png)