130. 被围绕的区域 - 力扣（LeetCode）

一、题目

给你一个 m x n 的矩阵 board ，由若干字符 'X' 和 'O' ，找到所有被 'X' 围绕的区域，并将这些区域里所有的 'O' 用 'X' 填充。

示例 1：

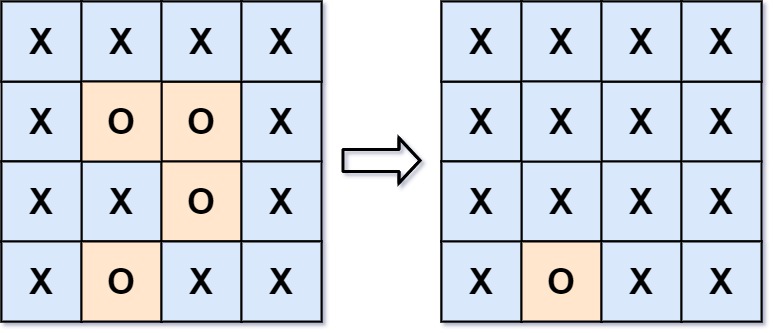
输入：board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
输出：[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
解释：被围绕的区间不会存在于边界上，换句话说，任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上，或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻，则称它们是“相连”的。

示例 2：
输入：board = [["X"]]
输出：[["X"]]

提示：

• m == board.length
• n == board[i].length
• 1 <= m, n <= 200
• board[i][j] 为 'X' 或 'O'

二、代码

class Solution {
    public void solve(char[][] board) {
        // 将连到上下两个边界的连成一片的O都感染成F
        for (int j = 0; j < board[0].length; j++) {
            if (board[0][j] == 'O') {
                infect(board, 0, j);
            }

            if (board[board.length - 1][j] == 'O') {
                infect(board, board.length - 1, j);
            }
        }

        // 将连到左右两个边界的连成一片的O都感染成F
        for (int i = 0; i < board.length; i++) {
            if (board[i][0] == 'O') {
                infect(board, i, 0);
            }

            if (board[i][board[0].length - 1] == 'O') {
                infect(board, i, board[0].length - 1);
            }
        }

        // 执行到这里，所有连接到边界的连成一片的O都改成了F，此时矩阵中仍然为O的，一定都是被X包围的

        // 遍历矩阵，将此时矩阵中为O的改成X，为F的再改回O，完成题目要求
        for (int i = 0; i < board.length; i++) {
            for (int j = 0; j < board[0].length; j++) {
                if (board[i][j] == 'O') {
                    board[i][j] = 'X';
                } else if (board[i][j] == 'F') {
                    board[i][j] = 'O';
                }
            }
        }
    }

    // 通过递归来进行感染过程，从(i,j)开始将连城一片的O改成F
    public void infect(char[][] board, int i, int j) {
        if (i < 0 || i >= board.length || j < 0 || j >= board[0].length || board[i][j] != 'O') {
            return;
        }

        board[i][j] = 'F';
        infect(board, i + 1, j);
        infect(board, i - 1, j);
        infect(board, i, j + 1);
        infect(board, i, j - 1);
    }
}

三、解题思路 

先开始绕着整个矩阵四周的边界开始感染，将从边界开始延伸连成一片的O都感染成F。

完成感染之后，此时只要是会连接到边界的那一片O都已经被感染成了F，还没有被感染成F的O一定都在矩阵内部，不和矩阵边界相连。所以再次遍历矩阵，遍历到的O一定都是没有从四周感染到的O，它一定是被X包裹的，将这些被X包裹的O在遍历过程中都改成X。最后再将矩阵中的F再改回O，就完成了将所有被 X 围绕的区域里所有的O用X填充。

for循环，在第0行边界和N-1行边界为O的位置开始往下、往上感染，将连成一片的O都改成F。
for循环，在左边界和右边界为O的位置开始往内感染，将连成一片的O都改成F。

此时与边界连通的练成一片的O就都改成F了，此时在矩阵中仍然为O的位置，就是完全被X包裹的O。最后遍历一遍矩阵，将此时矩阵中的O改成X，F改为O即可。

时间复杂度O(N*M)