MATLAB演示梯度上升寻找极值

梯度

梯度的本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。对于二元函数$f(x,y)$的梯度计算公式为：
$$\mathrm{gradf}(\mathrm{x},\mathrm{y})=\nabla f(x,y)=\left\{\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}\right\}=f_x(x,y)\bar{i}+f_y(x,y)\bar{j}$$
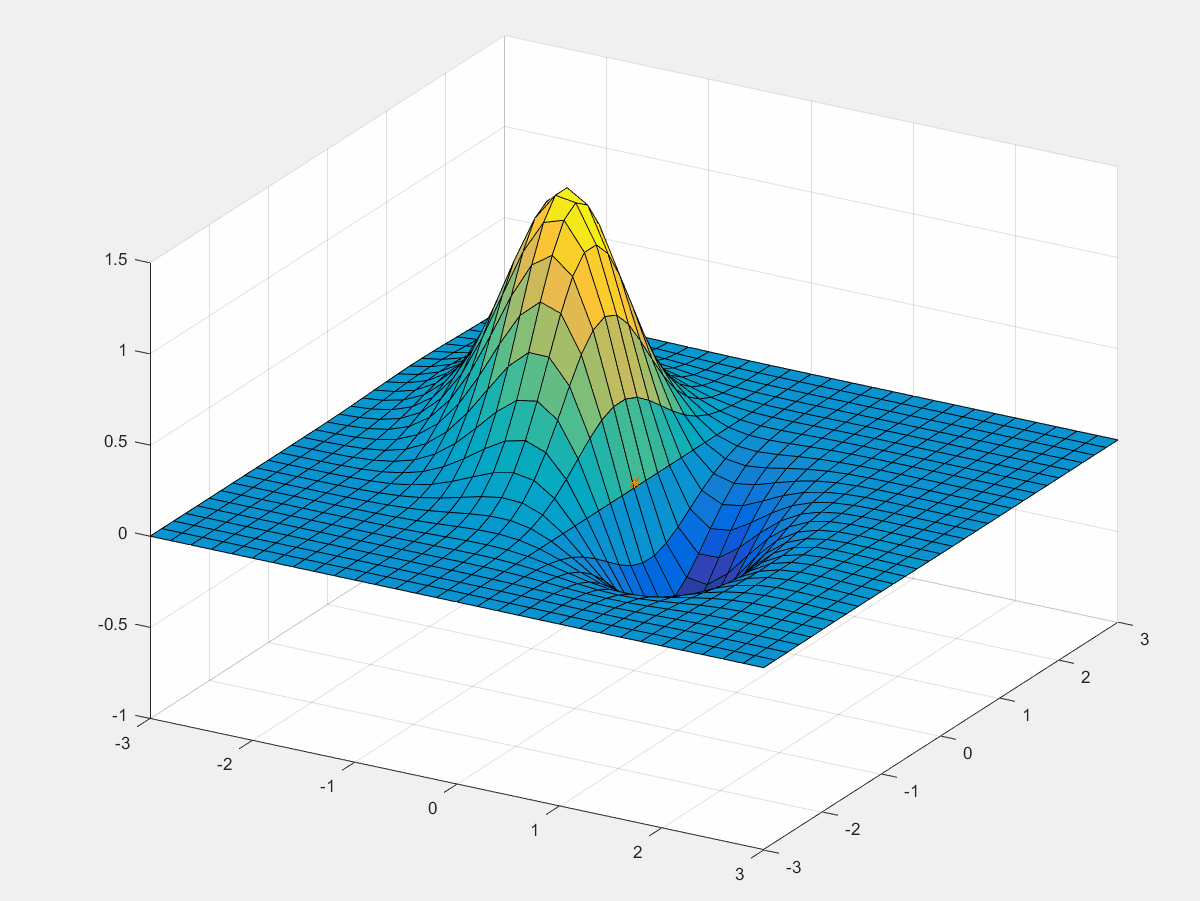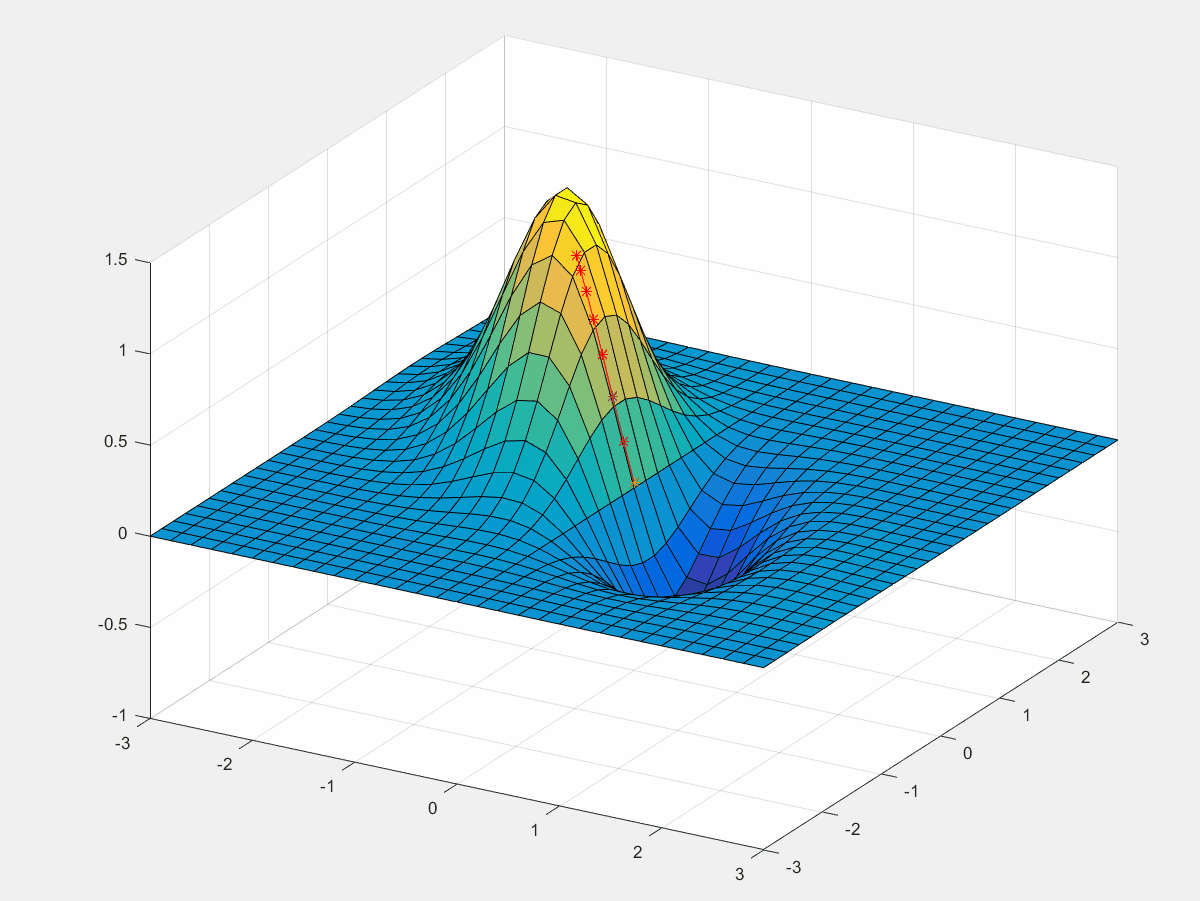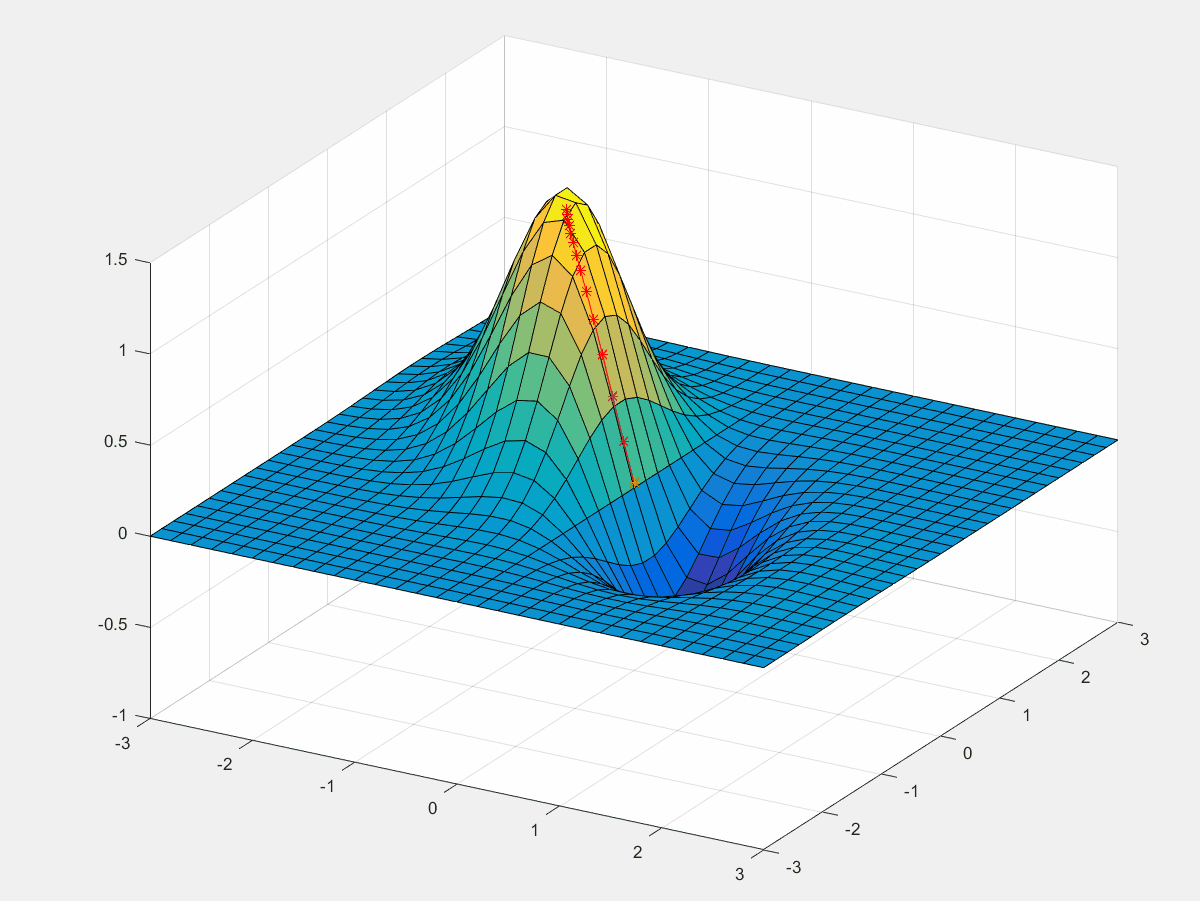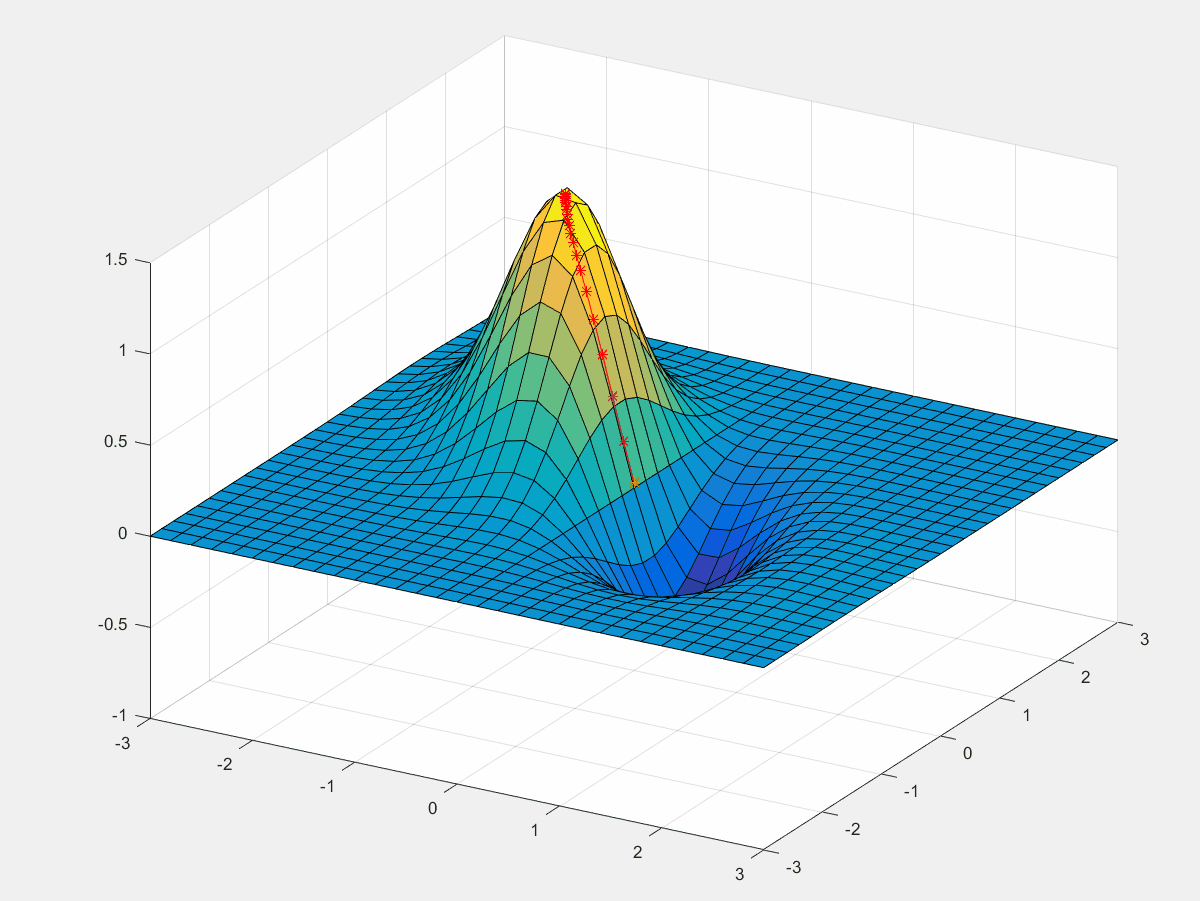
利用梯度求解以下函数的最大值，同时用MATLAB画出迭代过程。
$$z=f(x,y)=\left(x^2-2x\right){\mathrm{e}}^{-x^2-y^2-xy}$$
利用梯度的话，我们需要先求偏导。可以手算，也可以用MATLAB的符号推导功能。
$$\begin{array}{rl}z& =(x^2-2x)\cdot {\mathrm{e}}^{-x^2-y^2-xy}\\ \frac{\partial z}{\partial x}& =-2(1+x^3+(\frac{y}{2}-2)x^2+(-y-1)x){\mathrm{e}}^{-x^2-xy-y^2}\\ \frac{\partial z}{\partial y}& =-x(x+2y)(x-2){\mathrm{e}}^{-x^2-xy-y^2}\end{array}$$

syms x y
z = (x^2-2*x)*exp(-x^2-y^2-x*y);
zx = simplify(diff(z,x));
zy = diff(z,y);

朝着梯度的方向函数值的上升最快。先设定一个初始值$x_0=0,y_0=0$和步长$a=0.01$然后按照梯度的方向开始迭代上升。
$$\begin{array}{r}{x}_n=x_{n-1}+a\frac{\partial f}{\partial x_{n-1}}\\ y_n=y_{n-1}+a\frac{\partial f}{\partial y_{n-1}}\end{array}$$
MATLAB代码

f = @(x,y) (x.^2 - 2.*x).*exp(-x.^2-y.^2-x.*y);							% 目标函数
fx = @(x,y) -2.*(1+x.^3+(0.5.*y-2).*x.^2-(y+1).*x).*exp(-x.^2-x.*y-y.^2);	% x偏导
fy = @(x,y) -x.*(x+2.*y).*(x-2).*exp(-x.^2-x.*y-y.^2);					  % y偏导

[x0,y0] = meshgrid(-3:.2:3,-3:.2:3);
z0 = f(x0,y0);
figure
surf(x0,y0,z0)
view(30,30)		% 调整视角
hold on

[x,y,a] = deal(0,0,0.01);
z = f(x,y);
[tx,ty,tz] = deal(x,y,z+0.03);	% 纪录过程
h = plot3(tx,ty,tz,'r*-');
set(gcf,'Position',[200 200 1000 800])

for i = 1:100
    x = x + a*fx(x,y);	% x变量梯度上升
    y = y + a*fy(x,y);	% y变量梯度上升
    z = f(x,y);
    if mod(i,5) == 0
        pause(1);
        [tx,ty,tz] = deal([tx x],[ty y],[tz z+0.03]);
        h.XData = tx;
        h.YData = ty;
        h.ZData = tz;
    end
end