cigma<0,a>0   min cigma/(a)  决定出基变量

 

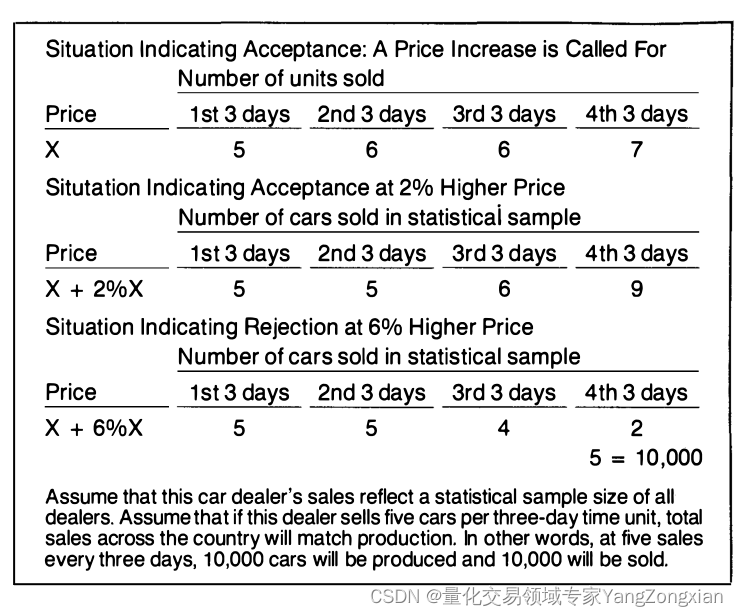
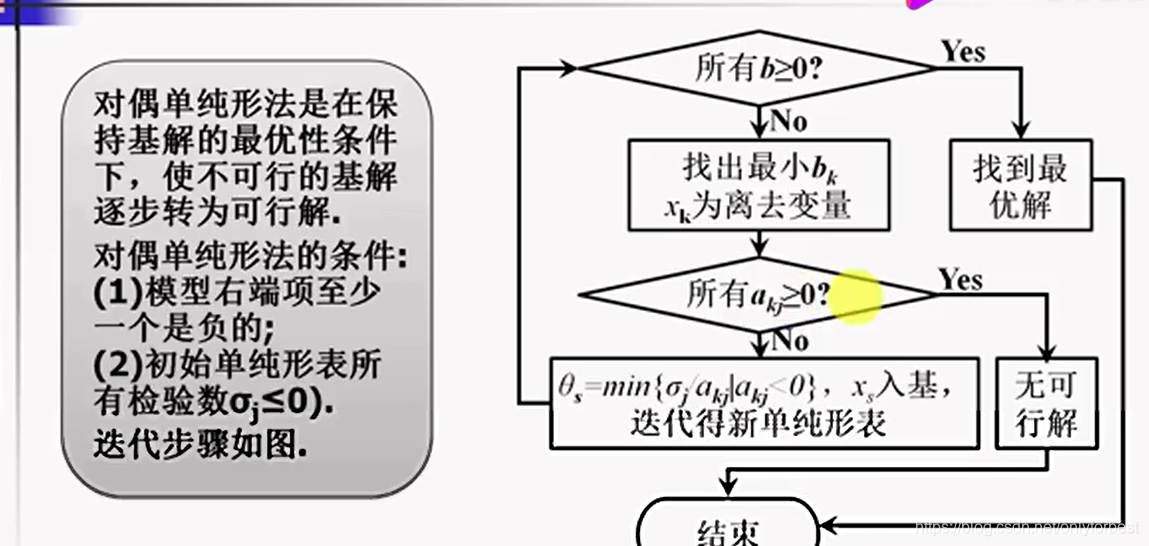
1对偶单纯形法 意思是看c就是所有货物的价值，去看一眼这些货物单价组合售卖的价值，这些价值肯定要都大于0，而且，组成这个c的系数也应该是都是正的，

c最小证明对min，贡献已经很大了，对于那些大的需要进一步优化，所以选择c最小的离开。

c最小的中找到，影响c下降最快的因素，让其作为解进一步影响其他组合，尽快降低其他的c，那么需要选择进去，
对偶的检验系数均<=0，那么就要看看到底是哪个因素造成了更大的负价值，cigma/a,cigma<0,a>0，a是数目，那么这个对总体价值的影响就比较大了,得到的值是负的，所以应该是选取最小的，这个负值最小，绝对值确实最大，是能够最快让目标函数极小化的关键因素，所以要选择他进行迭代。

如果所有的c 均>=0,那么结束，如果c,没有全>=0,但是a全都>=0,则证明是矛盾的

 

cigma>0,a<0   min cigma/(-a)  决定出基变量

单纯形法：

min : cigma<=0,还有减小的可能 ，选取最小的作为进基变量，  b/a a>0,选取最小的比值出基变量。

max : cigma>=0,还有增大的可能 ，选取最大的作为进基变量，  b/a a>0,选取最小的比值出基变量。

 

 

cigma>0证明还有可以提升最大利润的空间，所以选择该因素进入利润最大化的规划，

 

那么要选择b/a中最大的，a是价值系数，a越大，说明，这部分利润大，选取最小比值，说明利润大的因素，却数量少，也就是该因素虽然系数很大，但是起作用很小。