给定一颗树，树中包含 n个结点（编号 1∼n）和 n−1条无向边。

请你找到树的重心，并输出将重心删除后，剩余各个连通块中点数的最大值。

重心定义：重心是指树中的一个结点，如果将这个点删除后，剩余各个连通块中点数的最大值最小，那么这个节点被称为树的重心。

输入格式

第一行包含整数 n，表示树的结点数。
接下来 n−1行，每行包含两个整数 a和 b，表示点 a和点 b之间存在一条边。

输出格式

输出一个整数 m，表示将重心删除后，剩余各个连通块中点数的最大值。

数据范围

1≤n≤105

输入样例

9
1 2
1 7
1 4
2 8
2 5
4 3
3 9
4 6

输出样例：

4

这里我们首先需要确定的是我们的存储图的结构
这道题我们一定要用邻接表去存，如果不是邻接表的话，我们的会报memory limits的警告的。

然后这道题我们的思路就是图的深度优先遍历。
C++ 图的相关知识
当我们每遍历一个结点的时候，我们就将这个去掉这个节点之后，树所剩下的最大的连通块的大小给求出来。那我们怎么求呢？
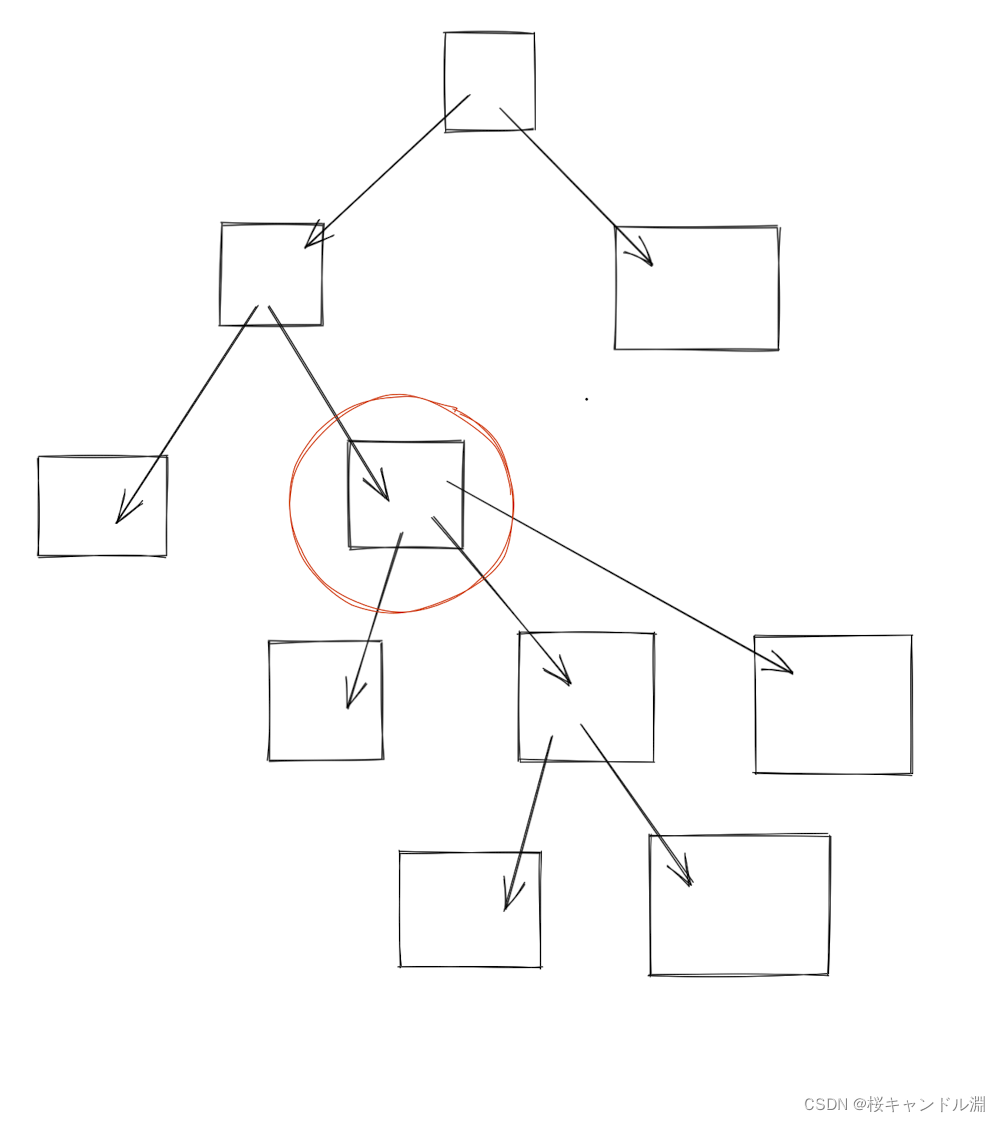
比方说我们当前遍历到了我们下面红色圈圈起来的这个节点，我们将其删掉，那么我们需要知道它的三个子树的结点个数s1,s2,s3。
然后只要我们将总的结点的个数减掉我们这个红圈的节点和s1,s2,s3，我们就能够得到这个红圈的上面的那一块连通图的结点个数s4，
然后我们只要从s1,s2,s3,s4中找到最大的那一个sx就可以了。

然后对于每一个节点的sx，我们只需要找到最小的那一个smin并返回就可以了。

#include<iostream>
#include<vector>
#include<list>
using namespace std;
//定义我们的邻接表
vector<list<int>> record(1e5+10,list<int>{});
//创建一个记录有没有访问过的数组
vector<bool> visited(1e5+10,false);
int number;
int ans=1e5+10;
//用于添加我们的节点到邻接表中
//这里最好是头插到链表，这用时间复杂度比较小，否则容易超时
void add(int a,int b)
{
    record[a].push_front(b);
}

int dfs(int u){
//res是用来记录我们上面s1,s2,s3,s4中最小的那一个的
    int res=0;
    //标记当前节点已读
    visited[u]=true;
    //初始我们的sum就是1，因为我们当前的结点已经算进去了
    //sum是以当前节点为根的树的结点个数的和
    //主要是用于返回给上一层用的
    int sum=1;
    //按照邻接表遍历每一个结点
    for(auto &i:record[u])
    {
        int j=i;
        if(!visited[j])
        {
            int s=dfs(j);
            //寻找s1,s2,s3,s4中最大的那一个
            res=max(res,s);
            //计算节点和
            sum+=s;
        }
    }
    res=max(res,number-sum);
    //ans用来查找我们上面所说的smin
    ans=min(res,ans);
    return sum;
}
int main()
{

    cin>>number;
    int i=0;
    //注意这里我们的输入的边只有n-1条
    while(i++<number-1)
    {
        int n,m;
        cin>>n>>m;
        //注意我们的无向图的话，我们需要添加双向的边
        add(n,m);
        add(m,n);
    }
    //这里我们随便选一个节点进行深度优先遍历就可以了。
    dfs(1);
    cout<<ans<<endl;
    return 0;
}