什么是支持向量机?
支持向量机(Support Vector Machine,SVM)是一种在机器学习领域中用于分类和回归分析的强大算法。它是一种监督学习算法,其目标是在特征空间中找到一个超平面,将不同类别的数据点分开,同时最大化分类边界的间隔。
SVM 的基本思想是找到能够有效划分数据的超平面,即在高维空间中的一个(d-1)维子空间,其中 d 是特征的数量。为了找到这个最佳的超平面,SVM 使用支持向量,即离超平面最近的一些数据点。这些支持向量决定了超平面的位置和方向。
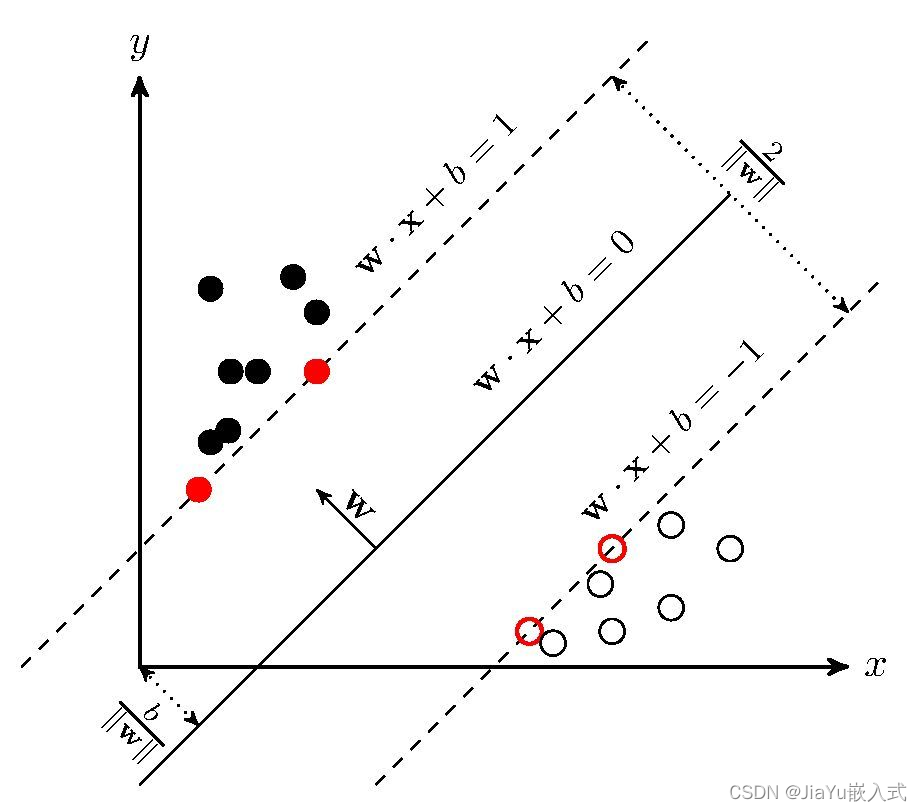
SVM 的优势在于它可以处理高维数据集,同时具有较强的泛化能力。它适用于线性和非线性分类问题,可以通过使用不同的核函数来处理非线性关系。常见的核函数包括线性核、多项式核、径向基函数(RBF)核等。
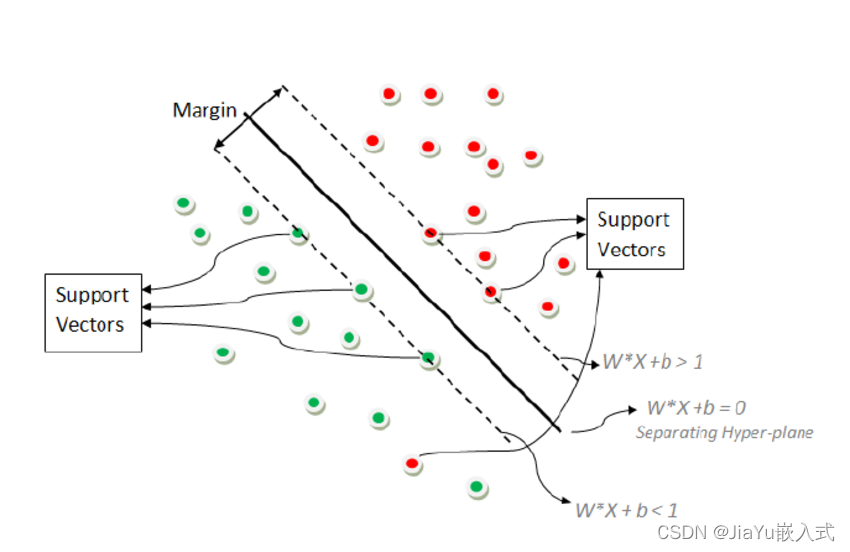
SVM 在解决小样本、非线性和高维数据的分类问题上表现出色,被广泛应用于图像分类、文本分类、生物信息学等领域。它是机器学习中的经典算法之一。
什么时候用支持向量机?
二分类问题: SVM 主要用于解决二分类问题,即将数据分成两个类别。通过在特征空间中找到一个超平面,SVM可以有效地进行二分类任务。
高维空间: 当数据具有大量特征时,SVM仍然能够有效工作。在高维空间中,SVM的性能通常比其他分类算法更好,这使其在处理图像、文本和生物信息学等领域的问题时非常有用。
小样本数据集: SVM 在小样本数据集上表现良好,因为它不依赖于整个数据集,而是依赖于支持向量。这使得它对于训练集规模相对较小的问题也适用。
非线性关系: SVM 可以通过使用核函数来处理非线性关系。常见的核函数包括多项式核、径向基函数(RBF)核等,使得 SVM 能够处理更加复杂的数据分布。
泛化能力强: SVM 在训练后具有较强的泛化能力,这意味着它在面对新的未见数据时能够产生较好的预测性能。
异常值敏感: SVM 对于异常值比一些其他算法更为鲁棒。由于它主要关注支持向量,对于远离超平面的离群点的影响相对较小。
图像分类和文本分类: SVM 在图像和文本分类等领域中被广泛应用。例如,在文本分类任务中,可以使用 SVM 对文本进行情感分析或主题分类。
总结
当面对复杂的、高维的数据集,并且需要一个能够提供良好泛化性能的分类器时,SVM是一个值得考虑的选择。然而,在处理大规模数据集时,训练时间可能会较长。
案例代码1
下面是一个简单的使用 Python 中的 Scikit-learn 库来实现支持向量机(SVM)模型的案例代码。这个例子使用一个虚拟的二维数据集,并演示了如何使用线性核的 SVM 进行分类。
# 导入必要的库
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 创建虚拟数据集
X, y = make_classification(n_samples=100, n_features=2, n_informative=2, n_redundant=0, random_state=42)
# 划分数据集为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 创建一个线性核的支持向量机模型
svm_model = svm.SVC(kernel='linear', C=1)
# 训练模型
svm_model.fit(X_train, y_train)
# 预测测试集
y_pred = svm_model.predict(X_test)
# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print(f"模型准确率: {accuracy}")
# 绘制决策边界
def plot_decision_boundary(model, X, y):
h = .02 # 步长
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=plt.cm.coolwarm, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.coolwarm)
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('SVM Decision Boundary')
plt.show()
# 绘制决策边界
plot_decision_boundary(svm_model, X_test, y_test)
这个例子中,使用了 Scikit-learn 中的 SVC 类创建了一个线性核的 SVM 模型,并使用虚拟数据集进行训练和测试。最后,我们计算了模型的准确率并绘制了决策边界。请注意,实际应用中,你可能需要根据问题的性质选择合适的核函数和调整模型参数。
案例代码2
from numpy import *
import random
import matplotlib.pyplot as plt
import numpy
def kernelTrans(X,A,kTup): # 核函数(此例未使用)
m,n=shape(X)
K = mat(zeros((m,1)))
if kTup[0] =='lin':
K=X*A.T
elif kTup[0]=='rbf':
for j in range(m):
deltaRow = X[j,:]-A
K[j]=deltaRow*deltaRow.T # ||w||^2 = w^T * w
K =exp(K/(-1*kTup[1]**2)) # K = e^(||x-y||^2 / (-2*sigma^2))
else:
raise NameError("Houston we Have a problem --")
return K
class optStruct:
def __init__(self,dataMain,classLabel,C,toler,kTup):
self.X = dataMain # 样本矩阵
self.labelMat = classLabel
self.C = C # 惩罚因子
self.tol = toler # 容错率
self.m = shape(dataMain)[0] # 样本点个数
self.alphas = mat(zeros((self.m,1))) # 产生m个拉格郎日乘子,组成一个m×1的矩阵
self.b =0 # 决策面的截距
self.eCache = mat(zeros((self.m,2))) # 产生m个误差 E=f(x)-y ,设置成m×2的矩阵,矩阵第一列是标志位,标志为1就是E计算好了,第二列是误差E
# self.K = mat(zeros((self.m,self.m)))
# for i in range(self.m): # K[,]保存的是任意样本之间的相似度(用高斯核函数表示的相似度)
# self.K[:,i]=kernelTrans(self.X,self.X[i,:],kTup)
def loadDataSet(filename): # 加载数据
dataMat = []
labelMat = []
fr = open(filename)
for line in fr.readlines():
lineArr = line.split()
dataMat.append([float(lineArr[0]),float(lineArr[1])])
labelMat.append(float(lineArr[2])) # 一维列表
return dataMat, labelMat
def selectJrand(i, m): # 随机选择一个不等于i的下标
j =i
while(j==i):
j = int(random.uniform(0,m))
return j
def clipAlpha(aj, H,L):
if aj>H: # 如果a^new 大于上限值,那么就把上限赋给它
aj = H
if L>aj: # 如果a^new 小于下限值,那么就把下限赋给它
aj = L
return aj
def calcEk(oS, k): # 计算误差E, k代表第k个样本点,它是下标,oS是optStruct类的实例
# fXk = float(multiply(oS.alphas,oS.labelMat).T * oS.K[:,k] + oS.b) # 公式f(x)=sum(ai*yi*xi^T*x)+b
fXk = float(multiply(oS.alphas,oS.labelMat).T * (oS.X*oS.X[k,:].T)) +oS.b
Ek = fXk - float(oS.labelMat[k]) # 计算误差 E=f(x)-y
return Ek
def selectJ(i, oS, Ei): # 选择两个拉格郎日乘子,在所有样本点的误差计算完毕之后,寻找误差变化最大的那个样本点及其误差
maxK = -1 # 最大步长的因子的下标
maxDeltaE = 0 # 最大步长
Ej = 0 # 最大步长的因子的误差
oS.eCache[i] = [1,Ei]
valiEcacheList = nonzero(oS.eCache[:,0].A)[0] # nonzero结果是两个array数组,第一个数组是不为0的元素的x坐标,第二个数组是该位置的y坐标
# 此处寻找误差矩阵第一列不为0的数的下标
print("valiEcacheList is {}".format(valiEcacheList))
if (len(valiEcacheList))>1:
for k in valiEcacheList: # 遍历所有计算好的Ei的下标,valiEcacheLIst保存了所有样本点的E,计算好的有效位置是1,没计算好的是0
if k == i:
continue
Ek = calcEk(oS,k)
deltaE = abs(Ei-Ek) # 距离第一个拉格朗日乘子a1绝对值最远的作为第二个朗格朗日乘子a2
if deltaE>maxDeltaE:
maxK = k # 记录选中的这个乘子a2的下标
maxDeltaE = deltaE # 记录他俩的绝对值
Ej = Ek # 记录a2此时的误差
return maxK, Ej
else: # 如果是第一次循环,随机选择一个alphas
j = selectJrand(i, oS.m)
# j = 72
Ej = calcEk(oS, j)
return j,Ej
def updateEk(oS, k):
Ek = calcEk(oS, k)
oS.eCache[k] = [1,Ek] # 把第k个样本点的误差计算出来,并存入误差矩阵,有效位置设为1
def innerL(i, oS):
Ei = calcEk(oS, i) # KKT条件, 若yi*(w^T * x +b)-1<0 则 ai=C 若yi*(w^T * x +b)-1>0 则 ai=0
print("i is {0},Ei is {1}".format(i,Ei))
if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)):
j,Ej = selectJ(i,oS,Ei)
print("第二个因子的坐标{}".format(j))
alphaIold = oS.alphas[i].copy() # 用了浅拷贝, alphaIold 就是old a1,对应公式
alphaJold = oS.alphas[j].copy()
if oS.labelMat[i] != oS.labelMat[j]: # 也是根据公式来的,y1 不等于 y2时
L = max(0,oS.alphas[j] - oS.alphas[i])
H = min(oS.C, oS.C+oS.alphas[j]-oS.alphas[i])
else:
L = max(0,oS.alphas[j]+oS.alphas[i]-oS.C)
H = min(oS.C,oS.alphas[j]+oS.alphas[i])
if L==H: # 如果这个j让L=H,i和j这两个样本是同一类别,且ai=aj=0或ai=aj=C,或者不同类别,aj=C且ai=0
# 当同类别时 ai+aj = 常数 ai是不满足KKT的,假设ai=0,需增大它,那么就得减少aj,aj已经是0了,不能最小了,所以此情况不允许发生
# 当不同类别时 ai-aj=常数,ai是不满足KKT的,ai=0,aj=C,ai需增大,它则aj也会变大,但是aj已经是C的不能再大了,故此情况不允许
print("L=H")
return 0
# eta = 2.0*oS.K[i,j]-oS.K[i,i]-oS.K[j,j] # eta=K11+K22-2*K12
eta = 2.0*oS.X[i,:]*oS.X[j,:].T - oS.X[i,:]*oS.X[i,:].T - oS.X[j,:]*oS.X[j,:].T
if eta >= 0: # 这里跟公式正好差了一个负号,所以对应公式里的 K11+K22-2*K12 <=0,即开口向下,或为0成一条直线的情况不考虑
print("eta>=0")
return 0
oS.alphas[j]-=oS.labelMat[j]*(Ei-Ej)/eta # a2^new = a2^old+y2(E1-E2)/eta
print("a2 归约之前是{}".format(oS.alphas[j]))
oS.alphas[j]=clipAlpha(oS.alphas[j],H,L) # 根据公式,看看得到的a2^new是否在上下限之内
print("a2 归约之后is {}".format(oS.alphas[j]))
# updateEk(oS,j) # 把更新后的a2^new的E更新一下
if abs(oS.alphas[j]-alphaJold)<0.00001:
print("j not moving enough")
return 0
oS.alphas[i] +=oS.labelMat[j]*oS.labelMat[i]*(alphaJold-oS.alphas[j]) # 根据公式a1^new = a1^old+y1*y2*(a2^old-a2^new)
print("a1更新之后是{}".format(oS.alphas[i]))
# updateEk(oS,i)
# b1^new = b1^old+(a1^old-a1^new)y1*K11+(a2^old-a2^new)y2*K12-E1
# b1 = oS.b-Ei-oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,i]-oS.labelMat[j]*\
# (oS.alphas[j]-alphaJold)*oS.K[i,j]
b1 = oS.b-Ei-oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.X[i,:]*oS.X[i,:].T-oS.labelMat[j]* \
(oS.alphas[j]-alphaJold)*oS.X[i,:]*oS.X[j,:].T
# b2 = oS.b-Ej-oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,j]-oS.labelMat[j]* \
# (oS.alphas[j]-alphaJold)*oS.K[j,j]
b2 = oS.b-Ej-oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.X[i,:]*oS.X[j,:].T-oS.labelMat[j]* \
(oS.alphas[j]-alphaJold)*oS.X[j,:]*oS.X[j,:].T
updateEk(oS,j) # 个人认为更新误差应在更新b之后,因为公式算出的b的公式使用的是以前的Ei
updateEk(oS,i)
# b2^new=b2^old+(a1^old-a1^new)y1*K12+(a2^old-a2^new)y2*K22-E2
if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]):
oS.b = b1.A[0][0]
elif (0<oS.alphas[j]) and (oS.C > oS.alphas[j]):
oS.b = b2.A[0][0]
else:
oS.b = (b1+b2)/2.0
print("b is {}".format(oS.b))
return 1
else:
return 0
def smoP(dataMatIn, classLabels, C,toler,maxIter,kTup=('lin',)):
oS = optStruct(mat(dataMatIn), mat(classLabels).transpose(),C,toler,kTup)
iter = 0
entireSet = True # 两种遍历方式交替
alphaPairsChanged = 0
while (iter<maxIter) and ((alphaPairsChanged>0) or (entireSet)):
alphaPairsChanged = 0
if entireSet:
for i in range(oS.m):
alphaPairsChanged += innerL(i,oS)
print("fullSet, iter:%d i: %d pairs changed %d"%(iter,i ,alphaPairsChanged))
iter+=1
print("第一种遍历alphaRairChanged is {}".format(alphaPairsChanged))
print("-----------eCache is {}".format(oS.eCache))
print("***********alphas is {}".format(oS.alphas))
print("---------------------------------------")
else:
nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0] # 这时数组相乘,里面其实是True 和False的数组,得出来的是
# 大于0并且小于C的alpha的下标
for i in nonBoundIs:
alphaPairsChanged += innerL(i,oS)
print("non-bound, iter: %d i:%d, pairs changed %d"%(iter,i,alphaPairsChanged))
print("第二种遍历alphaPairChanged is {}".format(alphaPairsChanged))
iter+=1
if entireSet:
entireSet = False # 当第二种遍历方式alpha不再变化,那么继续第一种方式扫描,第一种方式不再变化,此时alphachanged为0且entireSet为false,退出循环
elif (alphaPairsChanged==0):
entireSet=True
print("iteration number: %d"%iter)
return oS.b,oS.alphas
def calcWs(alphas,dataArr,classLabels): # 通过alpha来计算w
X = mat(dataArr)
labelMat = mat(classLabels).transpose()
m,n = shape(X)
w = zeros((n,1))
for i in range(m):
w += multiply(alphas[i]*labelMat[i], X[i,:].T) # w = sum(ai*yi*xi)
return w
def draw_points(dataArr,classlabel, w,b,alphas):
myfont = FontProperties(fname='/usr/share/fonts/simhei.ttf') # 显示中文
plt.rcParams['axes.unicode_minus'] = False # 防止坐标轴的‘-’变为方块
m = len(classlabel)
red_points_x=[]
red_points_y =[]
blue_points_x=[]
blue_points_y =[]
svc_points_x =[]
svc_points_y =[]
# print(type(alphas))
svc_point_index = nonzero((alphas.A>0) * (alphas.A <0.8))[0]
svc_points = array(dataArr)[svc_point_index]
svc_points_x = [x[0] for x in list(svc_points)]
svc_points_y = [x[1] for x in list(svc_points)]
print("svc_points_x",svc_points_x)
print("svc_points_y",svc_points_y)
for i in range(m):
if classlabel[i] ==1:
red_points_x.append(dataArr[i][0])
red_points_y.append(dataArr[i][1])
else:
blue_points_x.append(dataArr[i][0])
blue_points_y.append(dataArr[i][1])
fig = plt.figure() # 创建画布
ax = fig.add_subplot(111)
ax.set_title("SVM-Classify") # 设置图片标题
ax.set_xlabel("x") # 设置坐标名称
ax.set_ylabel("y")
ax1=ax.scatter(red_points_x, red_points_y, s=30,c='red', marker='s') #s是shape大小,c是颜色,marker是形状,'s'代表是正方形,默认'o'是圆圈
ax2=ax.scatter(blue_points_x, blue_points_y, s=40,c='green')
# ax.set_ylim([-6,5])
print("b",b)
print("w",w)
x = arange(-4.0, 4.0, 0.1) # 分界线x范围,步长为0.1
# x = arange(-2.0,10.0)
if isinstance(b,numpy.matrixlib.defmatrix.matrix):
b = b.A[0][0]
y = (-b-w[0][0]*x)/w[1][0] # 直线方程 Ax + By + C = 0
ax3,=plt.plot(x,y, 'k')
ax4=plt.scatter(svc_points_x,svc_points_y,s=50,c='orange',marker='p')
plt.legend([ax1, ax2,ax3,ax4], ["red points","blue points", "decision boundary","support vector"], loc='lower right') # 标注
plt.show()
dataArr,labelArr = loadDataSet('/home/zhangqingfeng/test/svm_test_data')
b,alphas = smoP(dataArr,labelArr,0.8,0.001,40)
w=calcWs(alphas,dataArr,labelArr)
draw_points(dataArr,labelArr,w,b,alphas)
数据集
可参考数据集
-0.397822 8.058397 -1
0.824839 13.730343 -1
1.507278 5.027866 1
0.099671 6.835839 1
-0.344008 10.717485 -1
1.785928 7.718645 1
-0.918801 11.560217 -1
-0.364009 4.747300 1
-0.841722 4.119083 1
0.490426 1.960539 1
-0.007194 9.075792 -1
0.356107 12.447863 -1
0.342578 12.281162 -1
-0.810823 -1.466018 1
2.530777 6.476801 1
1.296683 11.607559 -1
0.475487 12.040035 -1
-0.783277 11.009725 -1
0.074798 11.023650 -1
-1.337472 0.468339 1
-0.102781 13.763651 -1
-0.147324 2.874846 1
0.518389 9.887035 -1
1.015399 7.571882 -1
-1.658086 -0.027255 1
1.319944 2.171228 1
2.056216 5.019981 1
-0.851633 4.375691 1
-1.510047 6.061992 -1
-1.076637 -3.181888 1
1.821096 10.283990 -1
3.010150 8.401766 1
-1.099458 1.688274 1
-0.834872 -1.733869 1
-0.846637 3.849075 1
1.400102 12.628781 -1
1.752842 5.468166 1
0.078557 0.059736 1
0.089392 -0.715300 1
1.825662 12.693808 -1
0.197445 9.744638 -1
0.126117 0.922311 1
-0.679797 1.220530 1
0.677983 2.556666 1
0.761349 10.693862 -1
-2.168791 0.143632 1
1.388610 9.341997 -1
0.317029 14.739025 -1