Go Map

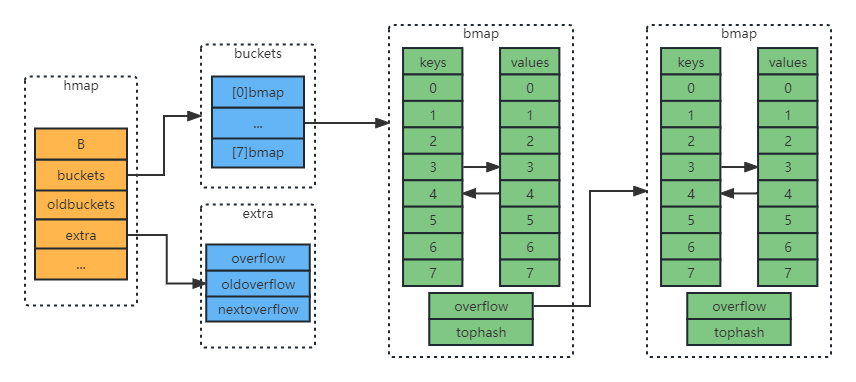
map 是一种key-value的键值对存储结构，其中key不能重复，无序。底层是hmap结构，hmap中维护buckets(bmap结构)。

结构定义

type hmap struct {
	count     int // 元素个数
	B         uint8  // buckets已扩容的次数，buckets长度2^B
	noverflow uint16 // 溢出buckets的数量
	hash0     uint32 // hash 种子
	buckets    unsafe.Pointer // 2^B buckets 的数组指针
	oldbuckets unsafe.Pointer // 指向扩容前的buckets的数组指针
	extra *mapextra // 可选字段，额外信息
}
// 额外信息
type mapextra struct {
	overflow    *[]*bmap
	oldoverflow *[]*bmap
	nextOverflow *bmap
}
// 在编译期间会产生新的结构体
type bmap struct {
	tophash [8]uint8 //存储哈希值的高8位
	data    byte[1]  //key value数据:key/key/.../value/value...
    overflow *bmap   //溢出bucket的地址
}

• bmap

backet数组中的每个元素都是bmap结构(本文都称为桶)
每个桶最多保存8个kv对，之后使用overflow连接下一个桶(溢出桶)。
tophash：保存的是key值哈希值的前8位，用作查找key的缓存，确定key是否存在
注：key、value、overflow字段都不显示定义，而是通过maptype计算偏移获取的。

• 高位hash和低位hash值

哈希函数会将传入的key值进行哈希运算，得到一个唯一的值。

比如key1的hash值为：0123456789876543210      
前八位hash值"01234567"部分就叫做"高位哈希值"，后B位hash值为"低位哈希值"

高位哈希值：是用来确定当前的桶有没有所存储的数据的
低位哈希值：是用来确定，当前的数据存在了哪个桶

查询

1. 根据key值算出哈希值
2. 取低位哈希值确定在哪号桶
3. 取高位哈希值在tophash数组中查询，确定在桶中的哪个位置
4. 对比key完整的哈希值，如匹配获取对应的value
5. 如没有找到，则从下个溢出桶中查找

存放

1. 根据key值算出哈希值
2. 取低位哈希值确定在哪号桶
3. 取高位哈希值在tophash数组中查询，确定在桶中的哪个位置
4. 对比key完整的哈希值，如匹配则更新值，不匹配则新增值
5. 如果当前桶元素已满，会通过overflow链接创建一个新的桶，来存储数据。

低位哈希值确定桶

Go通过'与运算法'来确定桶的位置
公式：hash(k)&(m-1),(m为map长度)
注：桶的数目需是2的整数次幂(m的二进制数不只含一个1)，否则会出现有些桶不会被选中

哈希冲突

Go通过'拉链法'来解决hash冲突:线性向下

• 查询冲突
  冲突原因：第3步找到对应高位哈希值，第4步对比完整哈希值时不同：
  解决方式：线性向下查找key值
• 存放冲突
  冲突原因：第3步找到对应高位哈希值，第4步对比完整哈希值时不同：
  解决方式：线性向下寻空位插入

负载因子

负载因子用于衡量一个哈希表冲突情况，公式为：负载因子 = 键数量 / 桶数量

• 哈希因子过小，说明空间利用率低
• 哈希因子过大，说明冲突严重，存取效率低

扩容

扩容有两种：等量扩容、2倍扩容

前提条件

1. 负载因子 > 6.5时，也即平均每个桶存储的键值对达到6.5个
2. 当溢出桶过多时：
   (map不断的put和delete key，桶中可能会出现很多断断续续的空位,会导致连接的bmap溢出桶很长，导致扫描时间边长)
   • 当B < 15 时，overflow的桶数量超过 2^B
   • 当B >= 15 时，overflow的桶数量超过 2^15

等量扩容

前提条件2：这种扩容实际上是一种整理，把后置位的数据整理到前面。这种情况下，元素会发生重排，但不会换桶。

2倍扩容

前提条件1：这种2倍扩容是由于当前桶数组确实不够用了，发生这种扩容时，元素会重排，可能会发生桶迁移。

• 扩容细节

1. 扩容刚发生时，会先将老数据存到oldbuckets里面。
2. 每次对map进行删改操作时，会触发从oldbucket中迁移到bucket的操作【非一次性，分多次】
3. 在扩容没有完全迁移完成之前，每次get或者put遍历数据时，都会先遍历oldbuckets，然后再遍历buckets。

线程不安全

• sync.Map
• map+互斥锁
• channel

优先使用互斥锁的场景：
1 复杂且频繁的数据读写操作，如：缓存数据；
2 应用中全局的共享数据，如：全局变量；

优先使用channel的场景：
1 协程之间局部传递共享数据，如：订阅发布模式；
2 统一的数据处理服务，如：库存更新+订单处理；

注意

• 对map数据进行操作时不可取地址，扩容会变
• map不会发生缩容：反复的扩容缩容会导致泄漏