并查集专题1

1.并查集介绍

并查集支持查询和合并操作，只回答两个节点是不是在一个连通分量中，并不回答路径问题。

如果一个问题具有传递性，可以考虑用并查集。并查集最常见的一种设计思想是把在同一个连通分量中的节点组织成一个树形结构。

2.并查集的核心函数

先搞明白模板里的函数——

首先在并查集类里常见的函数，初始函数、find()函数，union()函数。

def init(self, n):

初始函数里面参数是节点个数n，初始化节点的父节点集合self.father，初始时每个节点都是一个连通域，数据类型可用列表或字典；

在这里插入图片描述

根据题目要求可能还有联通区域的数量（初始有n个）；

在合并的时候如果是小树挂大树，那就用哈希表self.size表示每个联通区域的节点个数（用列表也行），key是根，value是节点个数，初始时每个联通区域大小都是1。主要是用在合并两个连通区域的时候判断哪个区域节点少，节点少的挂在节点多的根上。

在合并的时候如果是按秩合并，初始化都是0。在合并的时候秩小的指向秩大的。

def __init__(self, n):
    self.father = {i: i for i in range(n)}
    self.rank = [0]*n
    #self.size = {i: 1 for i in range(n)}
    self.cnt = n

def find(self, x):

find()函数是查找节点x的根节点。代码上可以用 father[x] = y 表示 x 的 father是 y，通过不断沿着搜索father找到x的 root。

def find(self, x):
    while x != self.fatehr[x]:
        x = self.father[x]
    return x

重点请注意，重点请注意，重点请注意。

并查集里有一个比较有意思的一点，就是能把查找的时间复杂度降低到接近常数级别，该操作是——路径压缩和按秩合并。

为什么这么说呢？

因为find是从当前节点往上搜索直到找到根节点，所以时间复杂度约等于树的高度，最差的情况为节点个数，find的时间复杂度降低到O(n)。如果进行路径压缩，树的高度不会超过logn。再结合按秩合并可以将时间复杂度降到趋近于O(1)。

路径压缩就是让节点直接指向根节点。
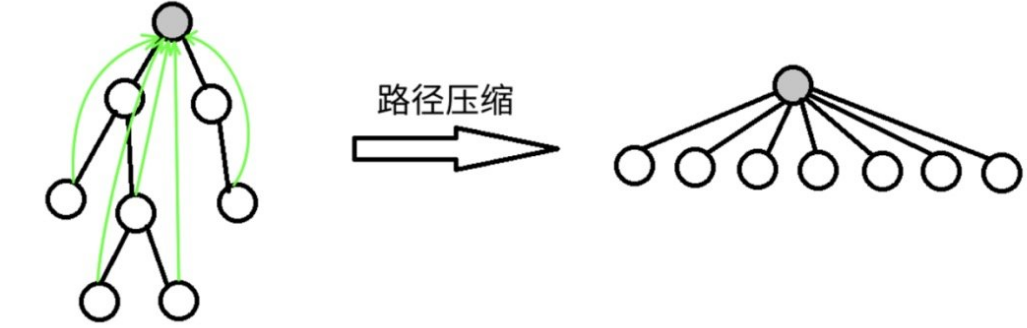
在这里插入图片描述

def find(self, x):
    if x == self.father[x]:
        return x
    # 路径压缩：让查找路径的每一个节点都指向根节点
    self.father[x] = self.find(self.father[x])
    return self.father[x]

def union(self, x,y):

union()函数是合并两个节点，先判断两个节点的根节点是不是同一个，不是的话，就把两个节点相连。

按秩合并就是在合并两个连通区域时使得合并后的树高度尽可能低，所以要将高度低的树指向高度高的树，也就是秩小的指向秩大的。这个秩我理解的就是树的高度。

def union(self, x, y):
   root_x, root_y = self.find(x), self.find(y)
   if root_x != root_y:
	   if self.rank[root_x] < self.rank[root_y]:
	       self.father[root_x] = root_y
	   else:
	       self.father[root_y] = root_x
	       # 两个秩相等因root_y指向root_x,故root_x的秩+1
	       if self.rank[root_x] == self.rank[root_y]:
	           self.rank[root_x] += 1

如果合并的时候是小树挂大树，代码就是：

def union(self, x: int, y: int):
    x, y = self.find(x), self.find(y)
    if x == y:
        return
    if self.size[x] < self.size[y]:
        x, y = y, x
    self.fathert[y] = x
    self.size[x] += self.size[y]

3.并查集模板

无权值模板

class Unionfind:
    """
    初始化函数
    self.father 哈希表 key是当前节点 value是该节点的根节点
    self.rank 是该节点所在联通区域的秩（高度）
    self.size 哈希表 key是联通区域的根节点 value是该联通区域节点个数
    self.cnt 是联通区域的个数
    """
    def __init__(self, n):
        self.father = {i: i for i in range(n)}
        self.rank = [0]*n
        # self.size = {i: 1 for i in range(n)}
        self.cnt = n
        
    """
    查找x节点的根节点
    路径压缩：经过的节点均指向根节点
    """
    def find(self, x):
        if x == self.father[x]:
            return x
        self.father[x] = self.find(self.father[x])
        return self.father[x]
    
    """
    合并两个连通区域
    按秩合并 小秩指向大秩
    """
    def union(self, x, y):
        root_x, root_y = self.find(x), self.find(y)
        if root_x != root_y:
            if self.rank[root_x] < self.rank[root_y]:
                self.father[root_x] = root_y
            else:
                self.father[root_y] = root_x
                if self.rank[root_x] == self.rank[root_y]:
                    self.rank[root_x] += 1

带权值模板

在初始化的时候再用一个哈希表存放权重。在路径压缩以及合并的时候都需要处理一下权重。

class Unionfindweight:
    """
    初始化函数
    self.father 哈希表 key是当前节点 value是该节点的根节点
    self.rank 是该节点所在联通区域的秩（高度）
    self.size 哈希表 key是联通区域的根节点 value是该联通区域节点个数
    self.cnt 是联通区域的个数
    """
    def __init__(self, n):
        self.father = {i: i for i in range(n)}
        self.rank = [0] * n
        self.weight = {i: 0 for i in range(n)}
        # self.size = {i: 1 for i in range(n)}
        self.cnt = n

    """
    查找x节点的根节点
    路径压缩：经过的节点均指向根节点
    """

    def find(self, x):
        if x != self.father[x]:
            root, w = self.find(self.father[x])
            self.father[x] = root
            self.weight[x] += w
        return self.father[x], self.weight[x]

    """
    合并两个连通区域
    """

    def union(self, x, y, w_xy):
        root_x, w_x = self.find(x)
        root_y, w_y = self.find(y)
        self.father[root_x] = root_y
        # 若x的根是a，y的根是b，则有w(xa) + w(ab) = w(xy) + w(yb)
        self.weight[root_x] = w_xy + w_y - w_x

4.实战实战

1319. 连通网络的操作次数

题目

用以太网线缆将 n 台计算机连接成一个网络，计算机的编号从 0 到 n-1。线缆用 connections 表示，其中 connections[i] = [a, b] 连接了计算机 a 和 b。

网络中的任何一台计算机都可以通过网络直接或者间接访问同一个网络中其他任意一台计算机。

给你这个计算机网络的初始布线 connections，你可以拔开任意两台直连计算机之间的线缆，并用它连接一对未直连的计算机。请你计算并返回使所有计算机都连通所需的最少操作次数。如果不可能，则返回 -1 。

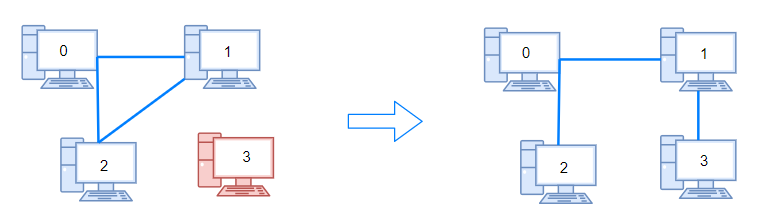
在这里插入图片描述

输入：n = 4, connections = [[0,1],[0,2],[1,2]]
输出：1
解释：拔下计算机 1 和 2 之间的线缆，并将它插到计算机 1 和 3 上。

思路和代码

用并查集，得到连通区域的个数，如果边的个数少于n-1，那么返回-1.否则返回的结果就是连通区域个数-1。

代码：

class Unionfind:
    def __init__(self, n):
        self.father = list(range(n))
        self.cnt = n
        self.rank = [0]*n

    def find(self, x):
        if x == self.father[x]:
            return x
        self.father[x] = self.find(self.father[x])
        return self.father[x]

    def union(self, x, y):
        root_x, root_y = self.find(x), self.find(y)
        if root_x == root_y:
            return 
        if self.rank[root_x] < self.rank[root_y]:
            self.father[root_x] = root_y
        else:
            self.father[root_y] = root_x
            if self.rank[root_x] == self.rank[root_y]:
                self.rank[root_x] += 1
        self.cnt -= 1

class Solution:
    def makeConnected(self, n: int, connections: List[List[int]]) -> int:
        if len(connections) < n-1:
            return -1
        uf = Unionfind(n)
        for node1,node2 in connections:
            uf.union(node1,node2)
        return uf.cnt -1

leetcode1971. 寻找图中是否存在路径

题目

有一个具有 n 个顶点的双向图，其中每个顶点标记从 0 到 n - 1（包含 0 和 n - 1）。图中的边用一个二维整数数组 edges 表示，其中 edges[i] = [ui, vi] 表示顶点 ui 和顶点 vi 之间的双向边。每个顶点对由最多一条边连接，并且没有顶点存在与自身相连的边。

请你确定是否存在从顶点 source 开始，到顶点 destination 结束的有效路径。

给你数组 edges 和整数 n、source 和 destination，如果从 source 到 destination 存在有效路径，则返回 true，否则返回 false 。

示例 1：

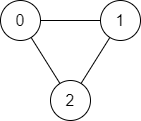
在这里插入图片描述

输入：n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2
输出：true
解释：存在由顶点 0 到顶点 2 的路径:

0 → 1 → 2
0 → 2

思路和代码

就判断source和destination在不在一个连通区域里嘛。

class Unionfind:
    def __init__(self, n):
        self.father = [i for i in range(n)]
        self.rank = [0] * n
    
    def find(self, x):
        if x == self.father[x]:
            return x
        self.father[x] = self.find(self.father[x])
        return self.father[x]
    
    def union(self,x,y):
        root_x, root_y = self.find(x), self.find(y)
        if root_x != root_y:
            if self.rank[root_x] < self.rank[root_y]:
                self.father[root_x] = root_y
            else:
                self.father[root_y] = root_x
                if self.rank[root_x] == self.rank[root_y]:
                    self.rank[root_x] += 1
    
    def connected(self,x,y):
        return self.find(x) == self.find(y)

            
class Solution:
    def validPath(self, n: int, edges: List[List[int]], source: int, destination: int) -> bool:
        uf = Unionfind(n)
        for node1, node2 in edges:
            uf.union(node1,node2)
        return uf.connected(source, destination)

547. 省份数量

题目
有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。

省份是一组直接或间接相连的城市，组内不含其他没有相连的城市。

给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。

返回矩阵中省份的数量。
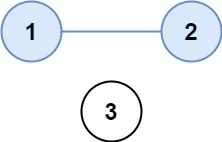
在这里插入图片描述

输入：isConnected = [[1,1,0],[1,1,0],[0,0,1]]
输出：2

思路和代码

直接套模板。

class Unionfind:
    def __init__(self, n):
        self.father = [i for i in range(n)]
        self.rank = [0] * n
        self.cnt = n
    
    def find(self, x):
        if x == self.father[x]:
            return x
        self.father[x] = self.find(self.father[x])
        return self.father[x]
    
    def union(self,x,y):
        root_x, root_y = self.find(x), self.find(y)
        if root_x != root_y:
            if self.rank[root_x] < self.rank[root_y]:
                self.father[root_x] = root_y
            else:
                self.father[root_y] = root_x
                if self.rank[root_x] == self.rank[root_y]:
                    self.rank[root_x] += 1
            self.cnt -= 1

class Solution:
    def findCircleNum(self, isConnected: List[List[int]]) -> int:
        n = len(isConnected)
        uf = Unionfind(n)
        for node1 in range(n):
            for node2 in range(n):
                if isConnected[node1][node2]==1:
                    uf.union(node1,node2)
        return uf.cnt

684. 冗余连接

题目
树可以看成是一个连通且无环的无向图。

给定往一棵 n 个节点 (节点值 1～n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间，且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ，edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。

请找出一条可以删去的边，删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案，则返回数组 edges 中最后出现的边。

示例 1：

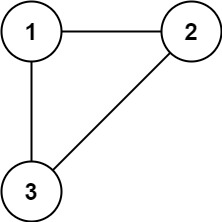
在这里插入图片描述
输入: edges = [[1,2], [1,3], [2,3]]
输出: [2,3]

思路和代码

判断图里是否有环，就是在union两个节点之前先判断是否已经连通，如果是的话则说明存在环。

代码：

class Unionfind:
    def __init__(self,n):
        self.father = [i for i in range(n+1)]
        self.rank = [0]*(n+1)
    
    def find(self,x):
        if x == self.father[x]:
            return x
        self.father[x] = self.find(self.father[x])
        return self.father[x]
    
    def union(self,x,y):
        x,y = self.find(x), self.find(y)
        if x != y:
            if self.rank[x] < self.rank[y]:
                self.father[x] = y
            else:
                self.father[y] = x
                if self.rank[x] == self.rank[y]:
                    self.rank[x] += 1
    
    def connected(self, x, y):
        return self.find(x) == self.find(y)

class Solution:
    def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
        n = len(edges)
        uf = Unionfind(n)
        for node1, node2 in edges:
            if uf.connected(node1,node2):
                return [node1,node2]
            uf.union(node1,node2)

参考文献：
1.https://github.com/azl397985856/leetcode/blob/master/thinkings/union-find.md（这个写的很好）
2.leetcode官网
3.https://blog.csdn.net/wait_nothing_alone/article/details/79254879
【算法】并查集—带路径压缩的按秩合并法