本文主要介绍了高斯滤波器的原理及其实现过程
高斯滤波器是一种线性滤波器,能够有效的抑制噪声,平滑图像。其作用原理和均值滤波器类似,都是取滤波器窗口内的像素的均值作为输出。其窗口模板的系数和均值滤波器不同,均值滤波器的模板系数都是相同的为1;而高斯滤波器的模板系数,则随着距离模板中心的增大而系数减小。所以,高斯滤波器相比于均值滤波器对图像个模糊程度较小。
什么是高斯滤波器
既然名称为高斯滤波器,那么其和高斯分布(正态分布)是有一定的关系的。一个二维的高斯函数如下:
h(x,y)=e−x2+y22σ2h(x,y)=e−x2+y22σ2
其中(x,y)(x,y)为点坐标,在图像处理中可认为是整数;σσ是标准差。要想得到一个高斯滤波器的模板,可以对高斯函数进行离散化,得到的高斯函数值作为模板的系数。例如:要产生一个3×33×3的高斯滤波器模板,以模板的中心位置为坐标原点进行取样。模板在各个位置的坐标,如下所示(x轴水平向右,y轴竖直向下)
这样,将各个位置的坐标带入到高斯函数中,得到的值就是模板的系数。
对于窗口模板的大小为 (2k+1)×(2k+1)(2k+1)×(2k+1),模板中各个元素值的计算公式如下:
Hi,j=12πσ2e−(i−k−1)2+(j−k−1)22σ2Hi,j=12πσ2e−(i−k−1)2+(j−k−1)22σ2
这样计算出来的模板有两种形式:小数和整数。
- 小数形式的模板,就是直接计算得到的值,没有经过任何的处理;
- 整数形式的,则需要进行归一化处理,将模板左上角的值归一化为1,下面会具体介绍。使用整数的模板时,需要在模板的前面加一个系数,系数为1∑(i,j)∈wwi,j1∑(i,j)∈wwi,j,也就是模板系数和的倒数。
高斯模板的生成
知道模板生成的原理,实现起来也就不困难了
void generateGaussianTemplate(double window[][11], int ksize, double sigma)
{
static const double pi = 3.1415926;
int center = ksize / 2; // 模板的中心位置,也就是坐标的原点
double x2, y2;
for (int i = 0; i < ksize; i++)
{
x2 = pow(i - center, 2);
for (int j = 0; j < ksize; j++)
{
y2 = pow(j - center, 2);
double g = exp(-(x2 + y2) / (2 * sigma * sigma));
g /= 2 * pi * sigma;
window[i][j] = g;
}
}
double k = 1 / window[0][0]; // 将左上角的系数归一化为1
for (int i = 0; i < ksize; i++)
{
for (int j = 0; j < ksize; j++)
{
window[i][j] *= k;
}
}
}
需要一个二维数组,存放生成的系数(这里假设模板的最大尺寸不会超过11);第二个参数是模板的大小(不要超过11);第三个参数就比较重要了,是高斯分布的标准差。
生成的过程,首先根据模板的大小,找到模板的中心位置ksize/2。 然后就是遍历,根据高斯分布的函数,计算模板中每个系数的值。
需要注意的是,最后归一化的过程,使用模板左上角的系数的倒数作为归一化的系数(左上角的系数值被归一化为1),模板中的每个系数都乘以该值(左上角系数的倒数),然后将得到的值取整,就得到了整数型的高斯滤波器模板。
下面截图生成的是,大小为3×3,σ=0.83×3,σ=0.8的模板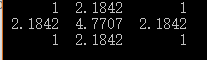
对上述解结果取整后得到如下模板:
116⎡⎣⎢121242121⎤⎦⎥116[121242121]