使用Numpy实现逻辑回归
sigmoid 函数
g ( z ) = 1 ( 1 + e − z ) g(z)=\frac{1}{(1+e^{−z} )} g(z)=(1+e−z)1
# sigmoid 函数
def sigmod(z):
return 1/(1+np.exp(-z))
线性计算与梯度下降
J ( θ ) = − 1 m [ ∑ i = 1 m y ( i ) l o g ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) l o g ( 1 − h θ ( x ( i ) ) ) ] J(θ)=-\frac{1}{m}[∑_{i=1}^m y^{(i)} log(h_θ(x^{(i)} ))+(1−y^{(i)}) log(1−h_θ (x^{(i)}))] J(θ)=−m1[i=1∑my(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]
对于代价函数,采用梯度下降算法求θ的最小值:
θ
j
≔
θ
j
−
α
∂
J
(
θ
)
∂
θ
j
θ_j≔θ_j−α\frac{∂J(θ)}{∂θ_j}
θj:=θj−α∂θj∂J(θ)
代入梯度:
θ
j
≔
θ
j
−
α
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
x
j
i
θ_j≔θ_j−α∑_{i=1}^m(h_θ (x^{(i)} )−y^{(i)} ) x_j^i
θj:=θj−αi=1∑m(hθ(x(i))−y(i))xji
# 进行计算
def compute(X,y,weights,bias):
count=len(X)
linear=np.dot(X,weights)+bias
predictions = sigmoid(linear)
dw=(1/count)*np.dot(X.T,(predictions-y))
db=(1/count)*np.sum(predictions-y)
return dw,db
def update(weights,bias,dw,db,rate):
weights=weights-rate*dw
bias=bias-rate*db
return weights,bias
实现逻辑回归
逻辑回归公式
h
θ
(
x
)
=
1
(
1
+
e
−
θ
T
X
)
h_θ (x)=\frac{1}{(1+e^{−θ^T X} )}
hθ(x)=(1+e−θTX)1
#逻辑回归
def logistic(X,y,rate,iterations):
count,col=X.shape
weights,bias=initialize(col)
for _ in range(iterations):
dw,db=compute(X,y,weights,bias)
weights,bias =update(weights,bias,dw,db,rate)
return weights, bias
测试模型
import numpy as np
import matplotlib.pyplot as plt
# 生成两个特征的单调数据
np.random.seed(42)
X1 = np.linspace(1, 5, 100) + np.random.randn(100) * 0.2
X2 = np.linspace(1, 5, 100) + np.random.randn(100) * 0.2
X = np.column_stack((X1, X2))
# 生成对应的标签,假设以直线 x1 = x2 为界限进行二分类
y = (X[:, 0] > X[:, 1]).astype(int)
# 添加偏置项
X_with_bias = np.c_[np.ones((X.shape[0], 1)), X]
# 训练逻辑回归模型
weights, bias = logistic(X_with_bias, y, rate=0.1, iterations=1000)
# 选择一些数据点进行预测
X_predict = np.array([[2, 2], [3, 4], [4, 3]])
predictions = predict(np.c_[np.ones((X_predict.shape[0], 1)), X_predict], weights, bias)
# 输出预测结果
print("Predictions:", predictions)
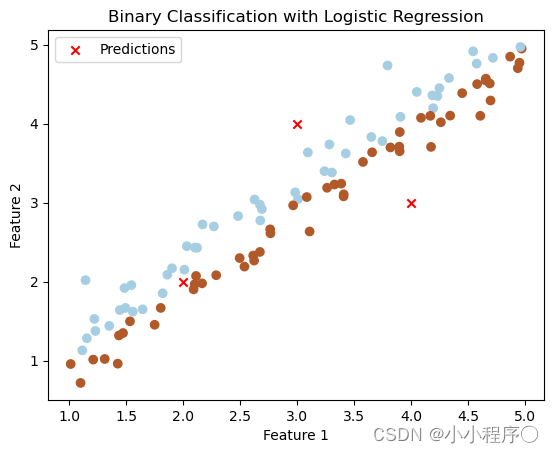
# 画出二分类后的图
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired, marker='o')
plt.scatter(X_predict[:, 0], X_predict[:, 1], marker='x', color='red', label='Predictions')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('Binary Classification with Logistic Regression')
plt.legend()
plt.show()
完整代码
import numpy as np
# sigmoid 函数
def sigmod(z):
return 1/(1+np.exp(-z))
# 初始化参数
def initialize(num_col):
weights=np.zeros(num_col)
bias=0
return weights,bias
# 进行计算
def compute(X,y,weights,bias):
count=len(X)
linear=np.dot(X,weights)+bias
predictions = sigmoid(linear)
dw=(1/count)*np.dot(X.T,(predictions-y))
db=(1/count)*np.sum(predictions-y)
return dw,db
# 梯度下降
def update(weights,bias,dw,db,rate):
weights=weights-rate*dw
bias=bias-rate*db
return weights,bias
#逻辑回归
def logistic(X,y,rate,iterations):
count,col=X.shape
weights,bias=initialize(col)
for _ in range(iterations):
dw,db=compute(X,y,weights,bias)
weights,bias =update(weights,bias,dw,db,rate)
return weights, bias
# 预测结果
def predict(X,weights,bias):
linear = np.dot(X,weights)+bias
predictions=sigmoid(linear)
return [1 if y_hat>0.5 else 0 for y_hat in predictions]
可视化代码
import numpy as np
import matplotlib.pyplot as plt
# 生成两个特征的单调数据
np.random.seed(42)
X1 = np.linspace(1, 5, 100) + np.random.randn(100) * 0.2
X2 = np.linspace(1, 5, 100) + np.random.randn(100) * 0.2
X = np.column_stack((X1, X2))
# 生成对应的标签,假设以直线 x1 = x2 为界限进行二分类
y = (X[:, 0] > X[:, 1]).astype(int)
# 添加偏置项
X_with_bias = np.c_[np.ones((X.shape[0], 1)), X]
# 训练逻辑回归模型
weights, bias = logistic(X_with_bias, y, rate=0.1, iterations=1000)
# 选择一些数据点进行预测
X_predict = np.array([[2, 2], [3, 4], [4, 3]])
predictions = predict(np.c_[np.ones((X_predict.shape[0], 1)), X_predict], weights, bias)
# 输出预测结果
print("Predictions:", predictions)
# 画出二分类后的图
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired, marker='o')
plt.scatter(X_predict[:, 0], X_predict[:, 1], marker='x', color='red', label='Predictions')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('Binary Classification with Logistic Regression')
plt.legend()
plt.show()