#include <iostream>
#include <bitset> 
using namespace std;
/*
向右的移位操作相当于丢掉最后的几位，然后剩下的位数进行“与”运算即可。
*/
int main()
{
    int a = 0x2FB7; //0x2FB7=0010 1111 1011 0111
    char end3 = (a >> 4) & 0x07; //取a的倒数第五、六、七位；
    char end2 = (a >> 2) & 0x03; //取a的倒数第三位、第四位；
    char end1 = (a>>1) & 0x01;   //取a的倒数第二位；
    char end0 = a & 0x01;        //取a的最后一位；
    cout << bitset<4>(end3) << endl;
    cout << bitset<4>(end2) << endl;
    cout << bitset<4>(end1) << endl;
    cout << bitset<4>(end0) << endl;

    return 0;
}

向右的移位操作相当于丢掉最后的几位，然后剩下的位数进行“与”运算即可。此处在进行计算时，选择转化成十六进制的数进行“与”运算，想要取n位比特，就对应的把二进制的n个1转化成十六进制的数，然后进行“与”运算即可。

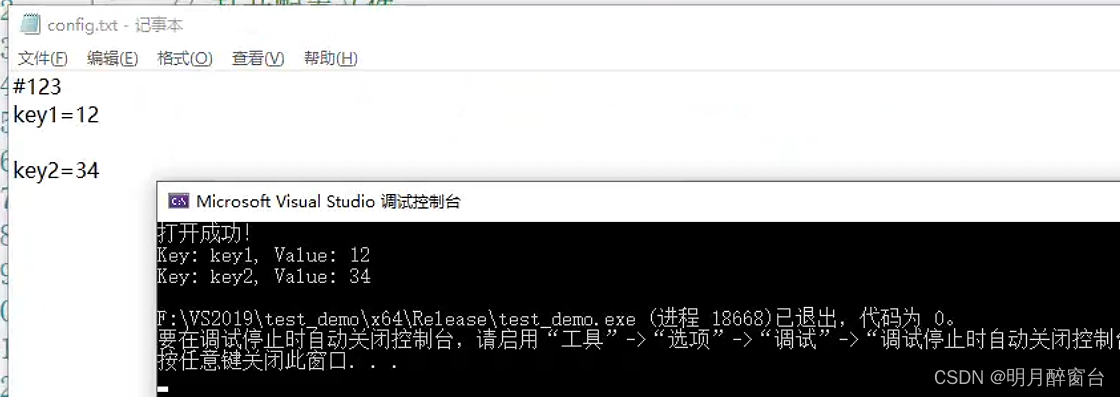
输出结果如下图所示：