贝叶斯网络（概率图模型）

定义

一种简单的用于表示变量之间条件独立性的有向无环图（DAG）。

主要考点

• 给出一定表述，要求画出贝叶斯网络图；
• 给出每个节点的条件概率表；
• 使用贝叶斯网络计算概率；
• 分析贝叶斯网络的独立性；

例题

- 要求画出贝叶斯网络图

臭鸡蛋（E）或灾难后动物的尸体（M）都会发出一种奇怪的臭味（S），灾难也可能导致海水沸腾（B）。

---

STEP1 先找出原因变量

E、M能导致S，所以E和M是原因变量，M也能导致B；因此由题目可以总结出E和M为原因变量，考虑首先把它们加入图中；

STEP2 依次把变量加入图中

首先加入E，然后加入M，E、M之间没有交互关系，无连接；
再加入S，E和M都能导致S，因此E和M都是S的父节点；
最后加入B，只有M能导致B，因此M作为B的父节点；
最后得出的贝叶斯网络图如下：

- 计算各节点的条件概率表

给定一定的数据集以及对应的贝叶斯网络，求各节点对应的条件概率表。

---

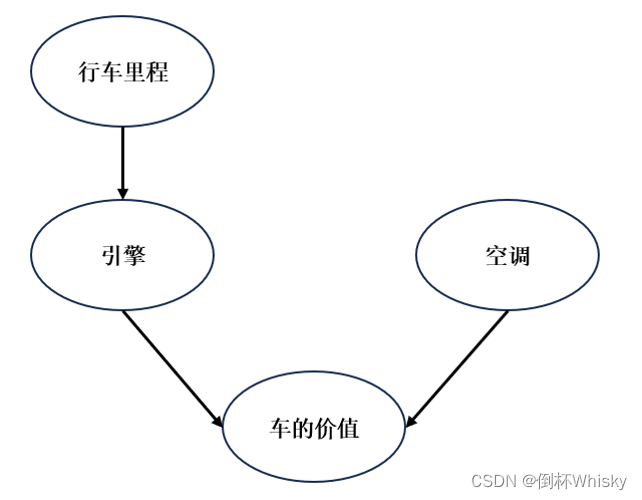
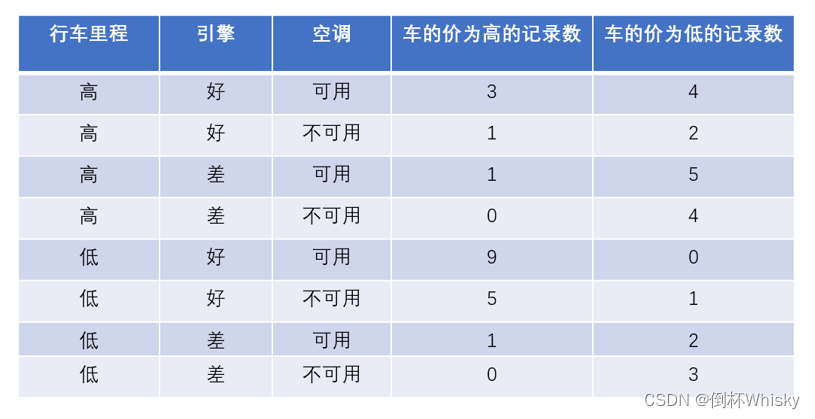
STEP1 首先处理无父节点的结点

• 对于行车里程，有高、低两种情况，概率各为0.5和0.5
  
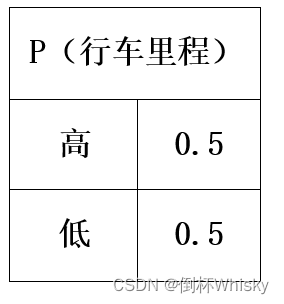
• 对于空调，有可用和不可用两种情况，概率都为0.5
  

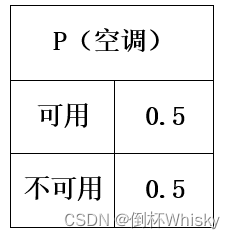
STEP2 再处理有父节点的结点

• 对于引擎，有一个父节点“行车里程”，因此条件概率表有四行
  
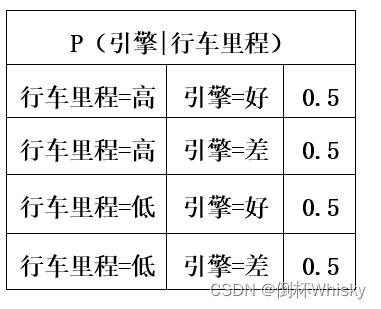
• 对于车的价值，有两个父节点，引擎和空调，因此有八行
  

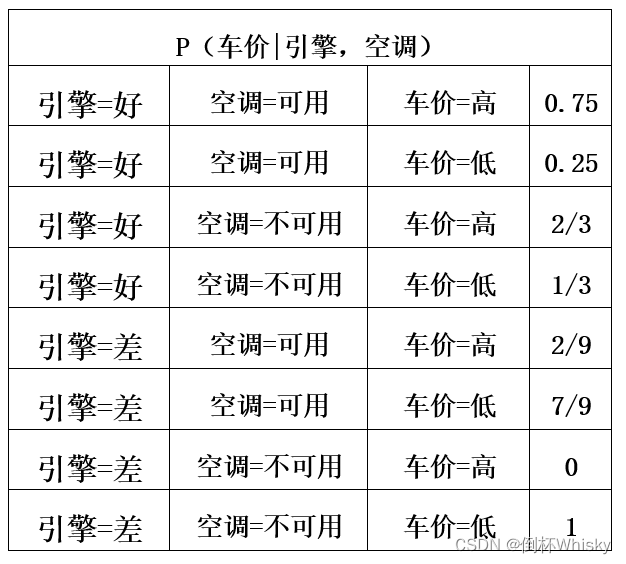
- 计算概率

在上一题的基础上计算P(引擎=差，空调=不可用)

P(引擎=差，空调=不可用)=∑_αβ P(引擎=差，空调=不可用，行车里程=α，车价=β)
=∑_αβ P(车价=β│引擎=差，空调=不可用)P(引擎=差 | 行车里程=α)P(行车里程=α)P(空调=不可用)=0.1453

臭鸡蛋（E）或灾难后动物的尸体（M）都会发出一种奇怪的臭味（S），灾难也可能导致海水沸腾（B）。
假定该表述的各条件概率表由下表所示，请计算出以下概率

---

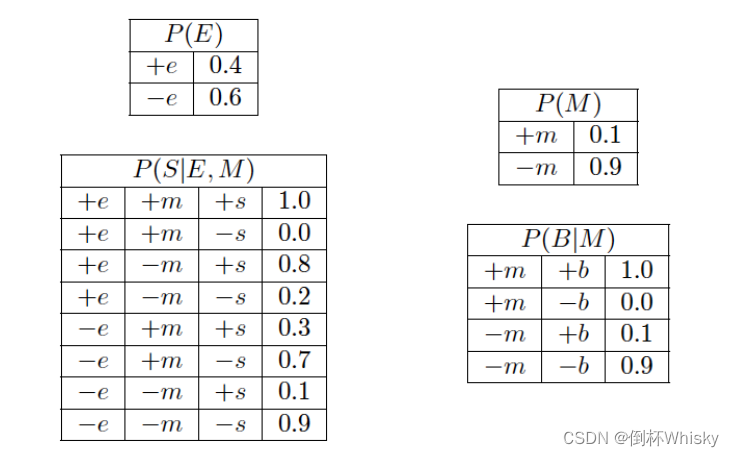
1、联合概率 P(-e,-s,-m,-b)

P(-e,-s,-m,-b) = P(-e)P(-m)P(-s|-e,-m)P(-b|-m) = 0.6×0.9×0.9×0.9 = 0.44

2、海水沸腾的概率 P(+b)

P(+b) = P(+b|+m)P(-m) + P(+b|-m)P(-m) = 1×0.1+0.1×0.9 = 0.19

3、在海水沸腾的条件下，动物尸体出现的概率 P(+m|+b)

P(+m|+b) = P(+b|+m)P(+m) / P(+b) = (1×0.1) / 0.19 = 0.53

4、在奇怪的臭味，海水沸腾与臭鸡蛋出现的条件下，动物尸体出现的概率 P(+m|+s,+b,+e)

分子部分：
P(+e,+s,+m,+b) = P(+e)P(+m)P(+s|+e,+m)P(+b|+m) = 0.4×0.1×1.0×1.0 = 0.04

分母部分

P(+s,+b,+e) = P(+e)P(+m)P(+s|+e,+m)P(+b|+m) + P(+e)P(-m)P(+s|+e,-m)P(+b|-m) = 0.4×0.1×1.0×1.0 + 0.4×0.9×0.8×0.1 = 0.0688

所以P(+m|+s,+b,+e) = 0.04/0.0688 = 0.58

- 分析独立性

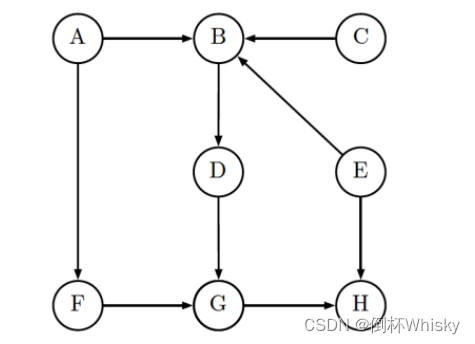
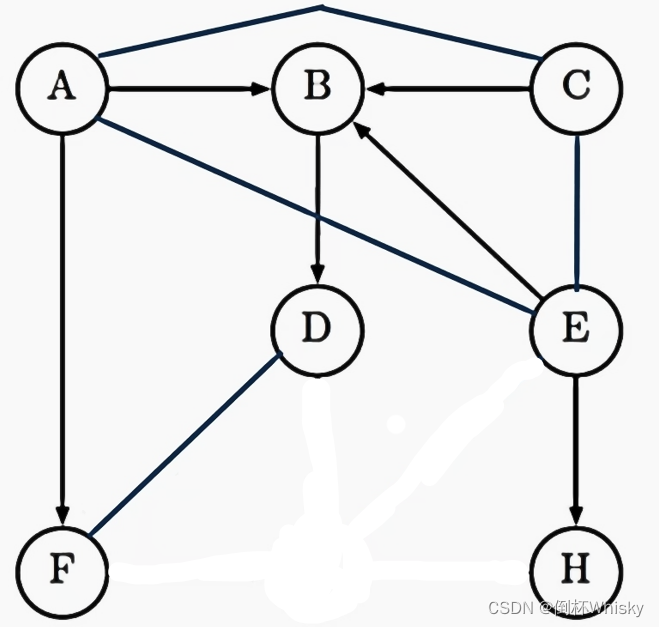
考虑下图所示的贝叶斯网络，判断以下表述是否正确

---

在做题之前讲一下如何判断独立性，有以下五个步骤

• 根据原始概率图，构建包括表达式中包含的变量以及这些变量的祖先节点的图；（这一步通常可以省略，看题目给出的图即可）
• 若两个节点有同一个子节点，连接这两个节点；（若一个变量的节点有多个父节点，则分别链接每一对父节点）
• 去掉图中所有的路径方向，将有向图变成无向图；
• 从图中删除需要判断的概率表达式中作为条件的变量，以及和它们相连的路径；
• 最后一步判断：若变量之间没有连接则独立，若有路径连接则不独立，若其中一个变量在上一步中被删掉了则独立。

下面我们结合五个表述来解释：
首先执行第二步，连接拥有同一个子节点的两个节点，然后第三步将有向图变为无向图（这一步因为懒就不画了）

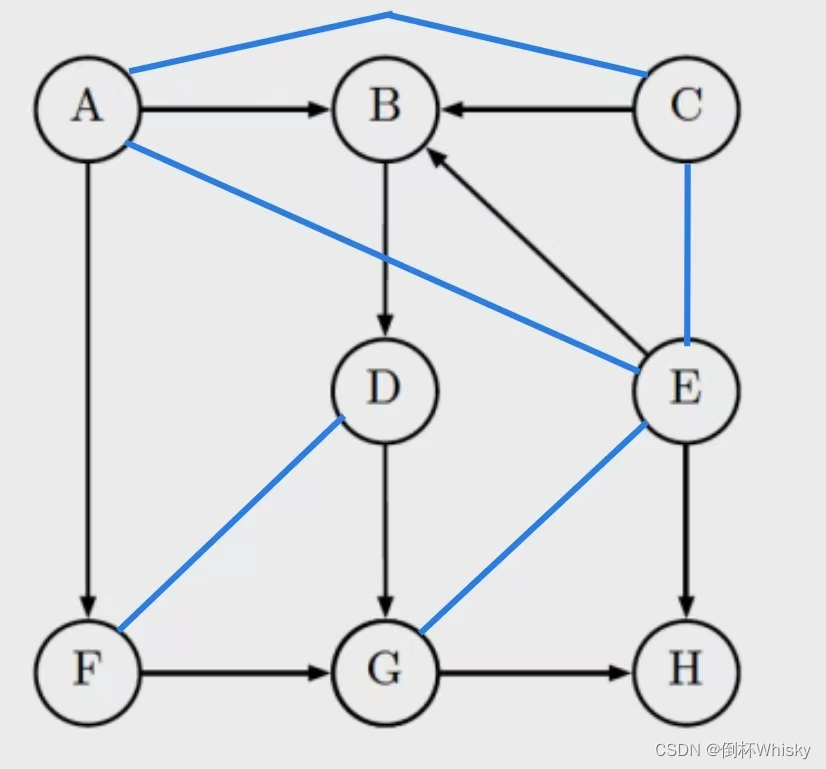
1、A$\perp \perp$B
由于该表述没有条件变量，所以第四步不用删除，我们只需判断A和B之间是否有连接，显然A和B是不独立的

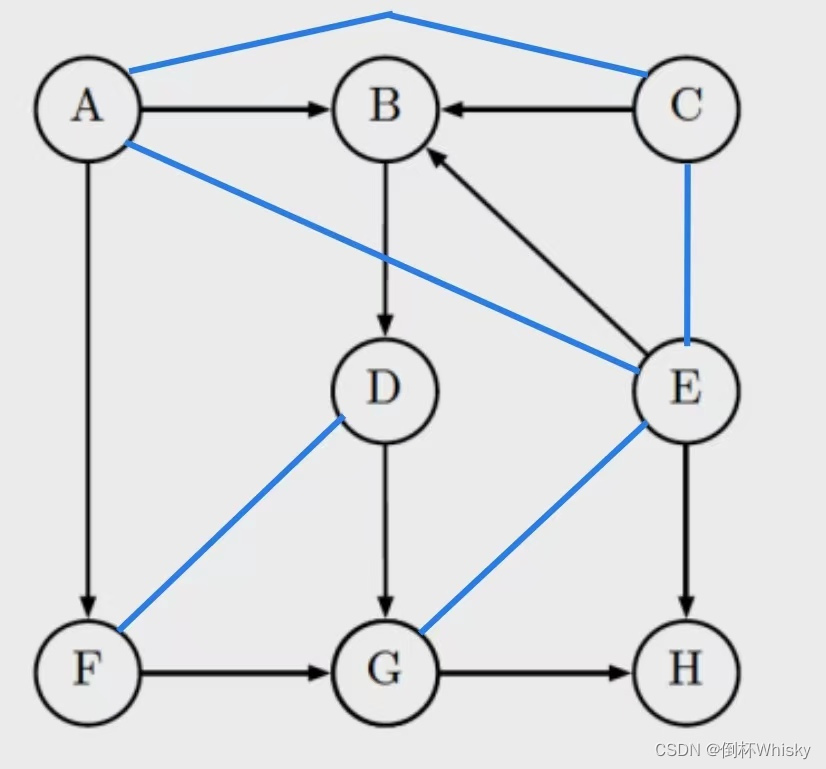
2、A$\perp \perp$D | {B , H}
这个表述有两个条件变量，所以我们需要删除B和H两个节点以及与它们相连的路径，变成下图

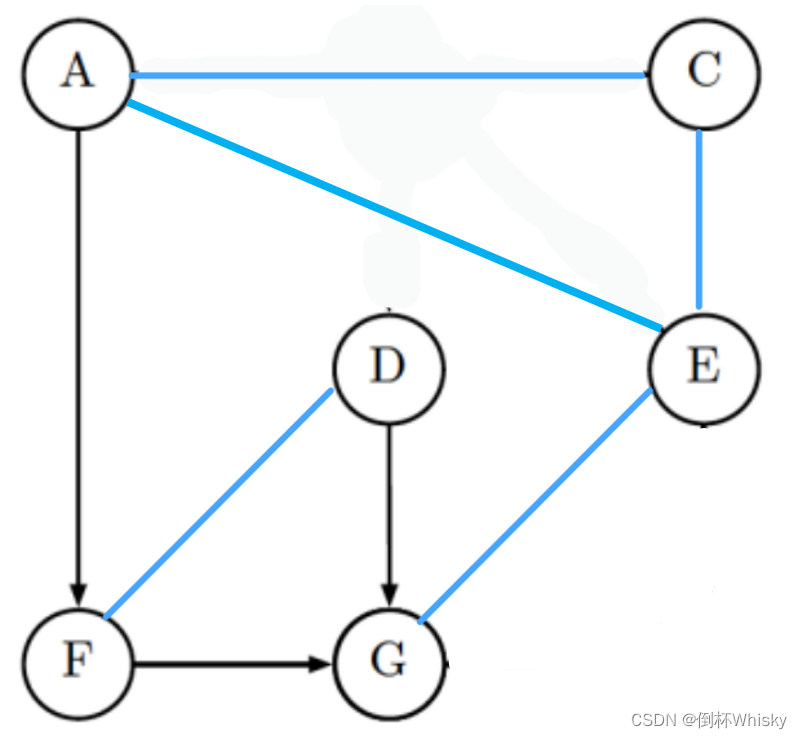
A和D之间没有连接，所以是独立的

3、G$\perp \perp$E | B
同理，删掉节点B和与B相连的路径，可以看到G和E之间是有连接的，所以G和E不独立

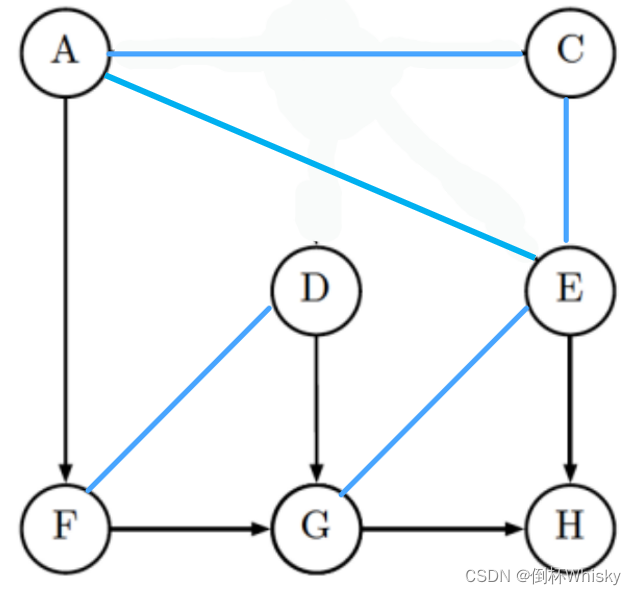
4、F$\perp \perp$C | D
删掉D，F和C之间没有连接，所以F和C是独立的

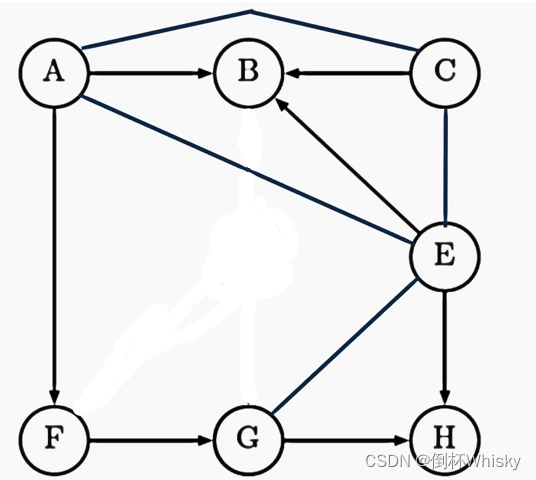
5、C$\perp \perp$H | G
删掉G，C和H之间没有连接，所以C和H是独立的

PS：但是这种方法好像有点问题，等我考完另一门试再来研究一下另一种方法

参考文章：
https://zhuanlan.zhihu.com/p/436214290
https://zhuanlan.zhihu.com/p/274314301