1、树的分类
(1)满二叉树
一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是(2^k)-1,则它就是满二叉树。
(2)完全二叉树
除最后一层外,若其余层都是满的,并且最后一层或者是满的,或者是在右边缺少连续若干节点,则这个二叉树就是完全二叉树。
(3)二叉查找树
二叉查找树,又叫做二叉排序树、二叉搜索树。
空树或者满足下列性质的二叉树:
1)若其左子树非空,则左子树上所有节点的值都小于根节点的值;
2)若其右子树非空,则右子树上所有节点的值都大于根节点的值;
3)其左右子树都是一棵二叉查找树。
(4)平衡二叉树
平衡二叉树,又称AVL树。它是一种特殊的二叉查找树。
空树或者满足下列性质的二叉查找树:
1)左子树和右子树的深度(高度)之差的绝对值不超过1;
2)其左右子树都是一颗平衡二叉树。
二叉树节点的平衡因子定义为该节点的左子树的深度减去右子树的深度,则平衡二叉树的所有节点的平衡因子只可能是-1、0、1。
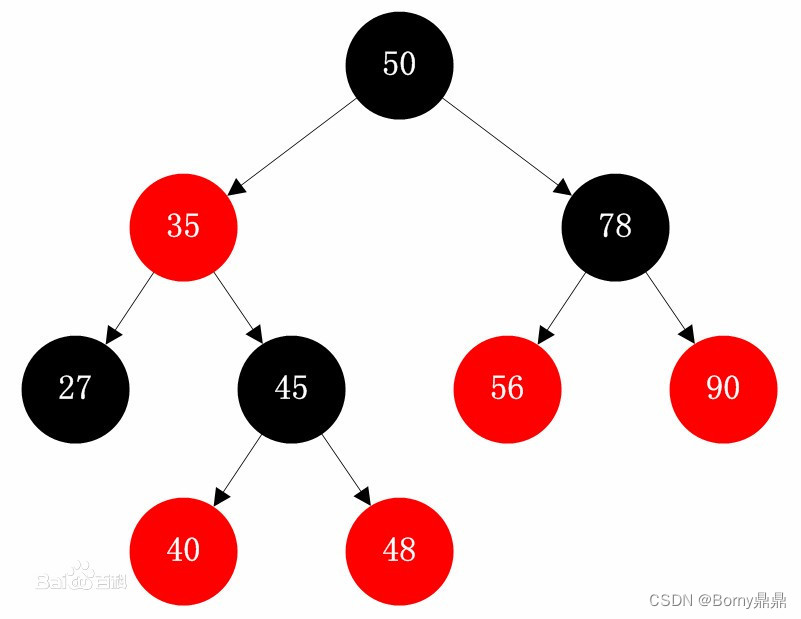
(5)红黑树
红黑树是每个结点都带有颜色属性的二叉查找树。
空树或者满足下列性质的二叉查找树:
1)节点不是黑色,就是红色(非黑即红);
2)根节点为黑色;
3)叶节点为黑色(叶节点是指末梢的空节点Nil或Null);
4)一个节点为红色,则其两个子节点必须是黑色的(根到叶子的所有路径,不可能存在两个连续的红色节点);
5)每个节点到叶子节点的所有路径,都包含相同数目的黑色节点(相同的黑色高度)。
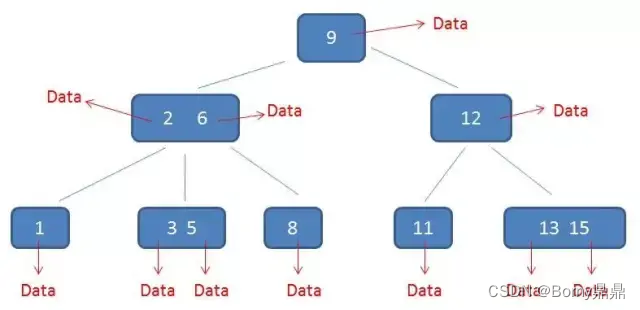
(6)B树
m阶可理解为m树,即内含(m-1)个关键字和m个子树。
一棵m阶B树是一棵平衡的m路搜索树。
B树又称B-树、B_树,一棵m阶的B树满足下列条件:
1)每个结点至多有m棵子树;
2)除根结点外,其它每个分支节点(非叶节点)至少有⌈m/2⌉(向上取整)棵子树;
3)根结点至少有两棵子树(除非B树只包含一个结点);
4)所有叶结点在同一层上,B树的叶结点可以看成一种外部结点,不包含任何信息;
5)有j个孩子的非叶结点恰好有j-1个关键码,关键码按递增次序排列。
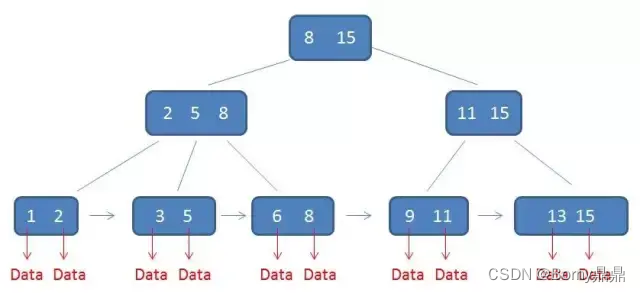
(7)B+树
B+树是应文件系统所需而产生的一种B树的变形树。一棵m阶的B+树和m阶的B树的差异在于:
1)有n棵子树的结点中含有n个关键码;
2)所有的叶子结点中包含了全部关键码的信息,及指向含有这些关键码记录的指针,且叶子结点本身依关键码的大小自小而大的顺序链接;
3)所有的非终端结点可以看成是索引部分,结点中仅含有其子树根结点中最大(或最小)关键码。
2、二叉树的存储
二叉树的存储主要分为链式存储和顺序存储两种。
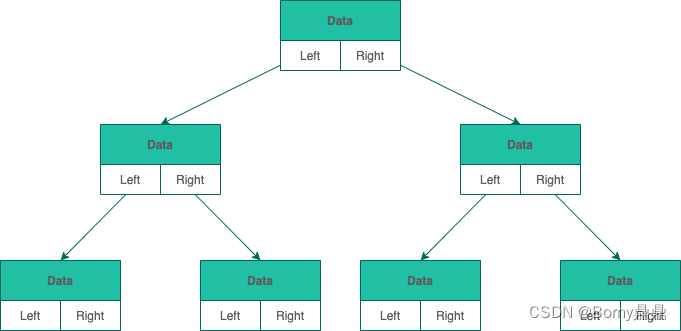
(1)链式存储
和链表类似,二叉树的链式存储依靠指针将各个节点串联起来,不需要连续的存储空间。
每个节点包括三个属性:
1)数据data。data不一定是单一的数据,根据不同情况,可以是多个具有不同类型的数据。
2)左节点指针left
3)右节点指针right。
(2)顺序存储
顺序存储就是利用数组进行存储,数组中的每一个位置仅存储节点的data,不存储左右子节点的指针,子节点的索引通过数组下标完成。根结点的序号为1,对于每个节点Node,假设它存储在数组中下标为i的位置,那么它的左子节点就存储在2i的位置,它的右子节点存储在下标为2i+1的位置。
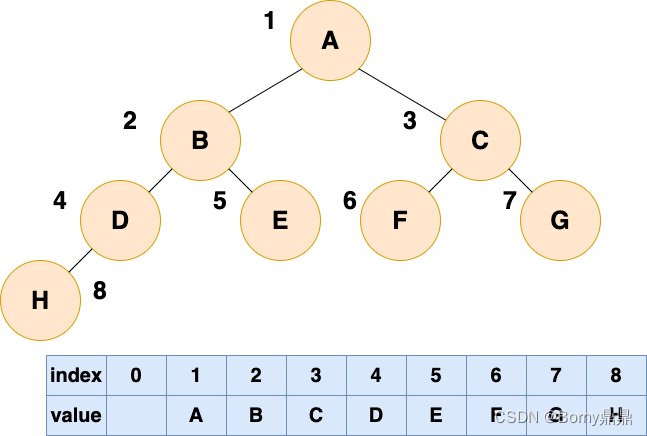
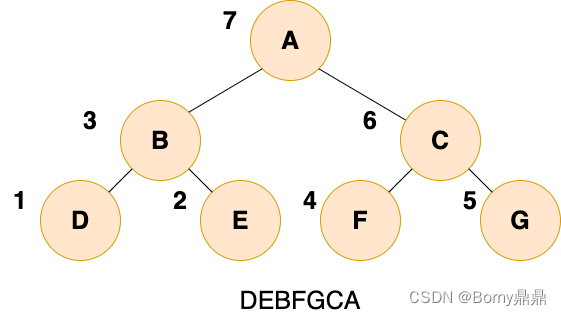
3、二叉树的遍历
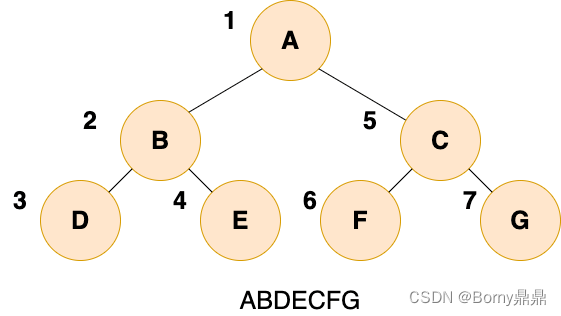
(1)先序遍历
二叉树的先序遍历,就是先输出根结点,再遍历左子树,最后遍历右子树,遍历左子树和右子树的时候,同样遵循先序遍历的规则。
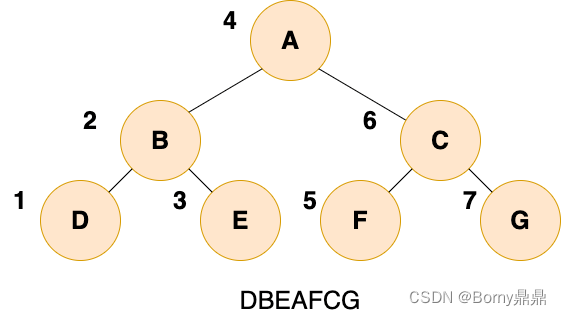
(2)中序遍历
二叉树的中序遍历,就是先递归中序遍历左子树,再输出根结点的值,再递归中序遍历右子树。
(3)后序遍历
二叉树的后序遍历,就是先递归后序遍历左子树,再递归后序遍历右子树,最后输出根结点的值。