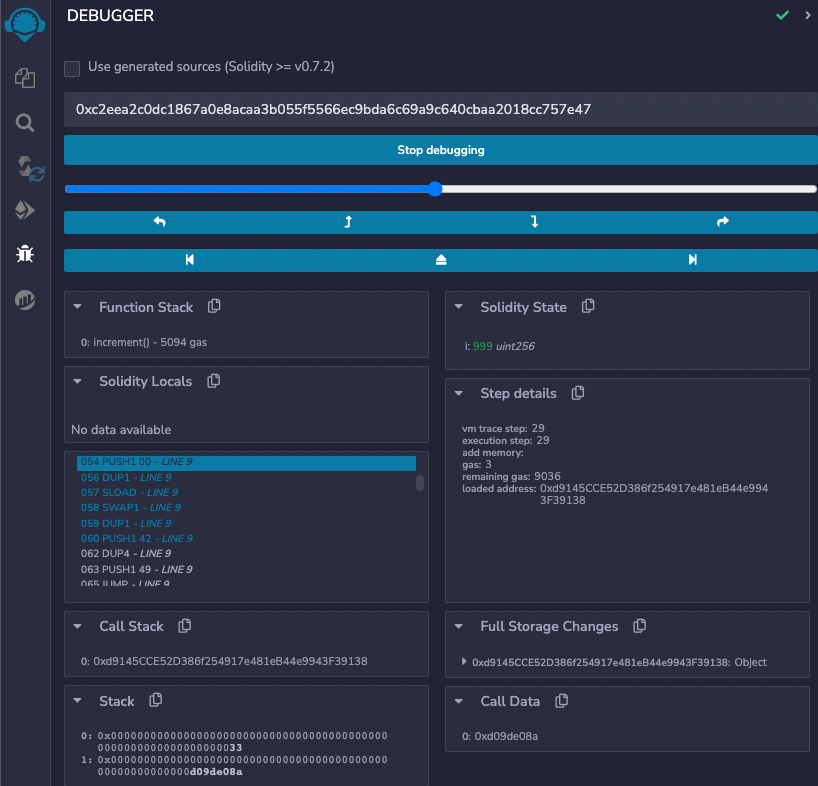
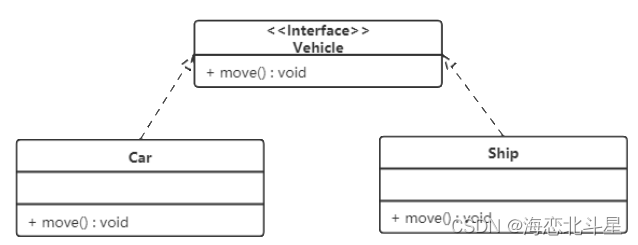
这节课的内容主要讲述如何通过插值等方式生成一条满足运动学约束的运动轨迹。这节的内容在全书中较少，相比前一章开链动力学而言，可以说内容少了许多。但是这节的内容却是目前在机械臂应用方面使用最广泛的一节。

闲话休提，马上开始：

定义

多项式插值

三次多项式与五次多项式

梯形运动

S曲线时间标度

Waypoint规划

时间最优的时间标度

时间标度算法

定义

文章中开篇就提及路径θ(s)和时间标度s(t)，看的让人有些迷糊，难道路径不是关于时间的函数吗？为什么要拆成两项。其实书中也提到，有时候也将时间选作s。这个可以用后面出现的一幅图很形象的说明：

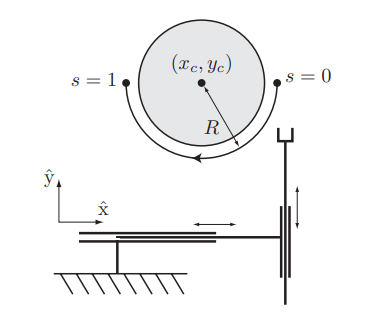
在这个图中，对于不同的s，xy不同，即所谓的θ(s)。而s又需要跟时间t相关才可以，因此才有了时间标度s(t)用来控制不同t时刻的s，从而得到对应的θ(s)。

我们可以把s取值范围设置为从0到1，那么直线运动和旋转运动就可以用如下的方式实现路径的插值：

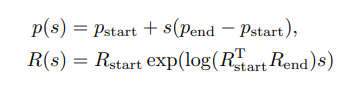
这种方式可以使得平移和旋转进行了解耦。

（不过实际我们工程上，对于旋转插值，一般采用四元数的球面线性插值slerp：四元数的球面线性插值（slerp） - 知乎，对于Eigen，用法则为：a.slerp(t,b)，即从t时间（0到1)从四元数a插值到四元数b）。

使用末端规划，可能存在两个问题：

1.路过奇异点附近，导致会生成不合理的关节速度。

2.两个可达端点的直线上的某些点可能无法到达。

多项式插值

三次多项式与五次多项式

这是最常用的机械臂轨迹生成的插值多项式，因为要满足机械臂的位置、速度与加速度的连续。

那么这里所谓的三次和五次是如何得到的？

以三次为例，

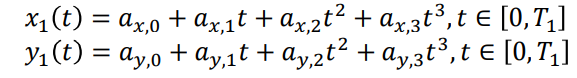
我们看到有四个未知数，如果保证起点和终点的位置、速度（位置的导数）连续，那么就相当于有四个方程。四个方程刚好对应四个未知数。

如果是要满足加速度连续，那就得再多两个式子，那么多项式里对应也多了a4t^4,a5t^5，则有六个未知数了。

如果想要保证加速度的导数jerk，jerk的导数snap也连续，也是同样的方法，只不过机械臂控制领域一般不用。保证加速度连续就可以了，这是因为根据牛顿定律f=ma原理，a连续则对应的力连续，力不突变就ok了。

那么如果我们想知道这些系数的话呢，就是解方程好了。

以五次多项式为例，将s(0)=0,s'(0)=0,s''(0)=0，s(T)=1,s'(T)=0,s''(T)=0代入：

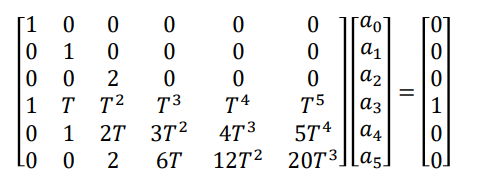
通过这个Ax=b的方程我就可以得到，T时间从点0静止出发到点1静止，插值所需的系数。

那么对于这种方程，如果周期T给定，那么就很好去求解，随便拿个numpy写两行代码就能求解了。

但是如果周期不是给定的，也希望它是个变量，并且想让求出的系数a里面也包含这个周期T呢？

当然，对于这种最简单的静止出发静止结束的，系数为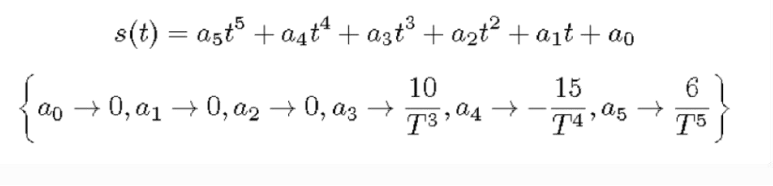：而其他的速度与加速度，则需要重新计算了：

import sympy as sym
import numpy as np
T = sym.symbols('T')
a=sym.symarray('a', 6)
b=sym.Matrix([0,0,0,1,0,0])
poly_T=sym.Matrix([[1,0,0,0,0,0], [0,1,0,0,0,0], [0,0,2,0,0,0], [1,T,T**2,T**3,T**4,T**5], [0,1,2*T,3*T**2,4*T**3,5*T**4], [0,0,2,6*T,12*T**2,20*T**3]])
inv_poly_T=poly_T.inv()
result=inv_poly_T*b
print(result)

sympy是python的一种符号式编程的库，也就是说，常规的方法只能计算出结果，不能得到一个表达式。但通过这种方式，就可以得到一个a关于T的表达式，非常好用，后续用处也很多，建议收藏。

梯形运动

3次、5次多项式虽然可以得到很平滑的运动轨迹，但是问题也很明显，在运动过程中是很可能产生突破关节速度和加速度的的运动轨迹的。

那么梯形运动则应运而生，这种思路就是先用最大加速度一路飙到最快，然后用最快的速度走，接着走用最大减速度减速，确保到达终点时速度为0。

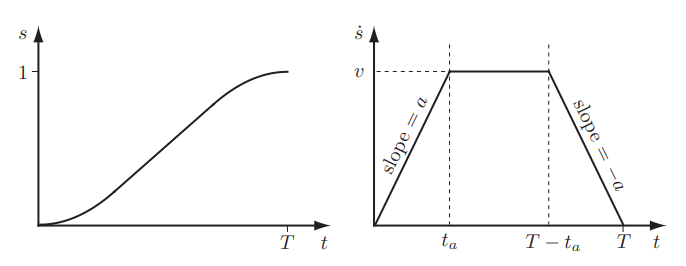
如果 $\frac{v^2}{a}>1$ ，即机器人永远不能达到速度v。梯形就变成了三角形。

$v^2>a$

$v^2t>at$

$v^2t>v$

$vt>1$

注意看上图的左图，s最大在s(T)的时候到达的是1位置，所以如果是这样的加速度，用v的速度运动任意时间都会导致移动距离大于1。

所以只有 $\frac{v^2}{a}\leq 1$ 的时候，才是梯形。

那么现在其实有四个参数，v，a，加速段t，总的时长T。这个可以根据用户自己的情况来确定。虽然是四个参数，t又是可以约掉的（因为v=at），所以这里就剩下三个参数v，a，T。

这里其实满足一个约束，因为最终运动的距离是1，所以vaT只能自己确定两个，剩下的一个由约束确定。

如果是确定v和a，那么时间T是：

如果确定v和T，那么加速度a是：

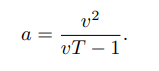
如果确定a和T，那么最大速度是：

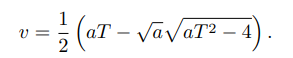
这些个公式方法具体是怎么算出来的，我呢不是很想关心，就不写原因了。

S曲线时间标度

上面的梯形运动其实对于机械臂不是很实用。因为机械臂最见不得加速度不连续，梯形运动会在拐角的地方发生加速度的突变。所以，通过S曲线方法，对拐角的地方进行一个平滑：

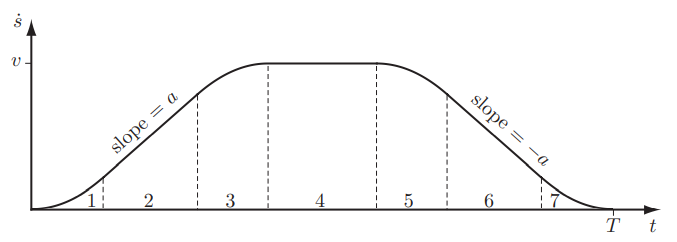
这7个阶段文字描述很拗口，但是一看图就知道含义，不再叙述了。

Waypoint规划

这个的目的是让机器人在指定时间通过一系列中间点，前后之间的路径形状则没有要求。

这部分书上写了一堆，其实都是废话。总归是套用上面的三次或者五次多项式插值方法，把中间的位置和速度填充进去即可。

这块还挺重要，比如刚好我们的项目最近有一块代码，实习生之前就是用五次多项式写的，多个过程衔接起来，中间减速（其实中间点减速到0是不需要的），显得整个过程有些笨重傻傻的。最近打算重构一下，现在也算复习了。

回到书本上，这块可以强调可以优化的点：

1.如果没有要求，中间点速度可以取得更合理一些，例如取上个点和下个点的平均速度方向，而并非到达此点时其速度一定要指向终点位置。

2.增加一些加速度的约束，或者对中间点的速度不指定，让它当成是自由的变量。

时间最优的时间标度

书这部分的内容看着似乎有些复杂，我简单总结下：

大多数机器人，随着路径不同，其实关节能提供的最大速度和加速度也是变化的。

把轨迹函数θ(s)和时间标度函数s(t)代入到动力学方程后，同时提供对机器人的约束（限制关节力矩），前者移项来满足后者，从而得到对加速度的限制。

我们令L是各组最小加速度中最大的那个，U为各组最大加速度中最小的那个，取中间的闭区间，即我们的加速度是要满足所有的关节，处于L和U之间。

我们在满足整个约束的情况下，找到s(t)，使得总时间T最小。

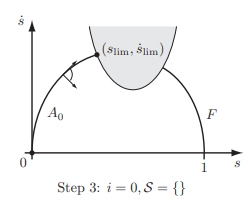
因此构建了一个 $(s,\dot{s})$ 相平面，即横坐标为位置s，纵坐标为速度。

1. 书中提到的“可行锥体”，即U和L箭头中间那个角度，如果相平面曲线的斜率刚好处于其中，则真正能提供这样的加速度。否则机械臂不能执行。

2. 在速度极限曲线以内，认为L>U，对了这里L可以理解为最大减速度，U理解为最大加速度。如果最大减速度居然大于最大加速度，那这地方不可行。

3. 对于速度极限曲线的切线，认为L=U。

时间标度算法

常规的方法是，先从终点用最大减速度L倒着走，再从起点用最大加速度U正着走，有个交点s*的地方就当成是开关，用这种方式就能让总行程时间T最小，并且还能满足机器人约束。

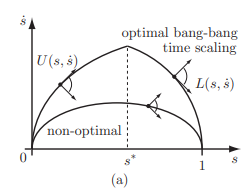
可是如果在上升途中碰到了速度极限曲线，交不到一起了，那怎么办？

这就是9.4.2节时间标度算法的内容了！

我依次介绍下：

先从s=1位置，用最大减速度L前向积分。

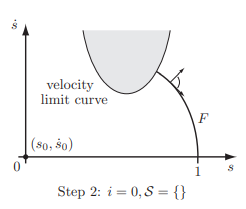
然后再从0位置用最大加速度往前走：

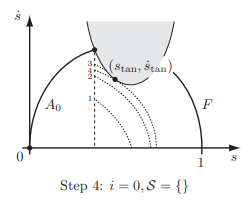
那这时候说明不能一直加速撞到速度极限曲线，应该在它之前就及时开启减速环节，因此在这里，对 $(s_{lim},\dot{s}_{lim})$ 的纵坐标采用2分法配合减速L来搜索哪个刚好能减速到和速度极限曲线相切：

找到这个 $(s_{tan},\dot{s}_{tan})$ 以后，就需从它开始，用最大减速度L倒着往前经过刚刚2分法的点，再往前，交于A0曲线，找到那个速度切换的开关s1。

s1就是减速的切换开关了，到 $(s_{tan},\dot{s}_{tan})$ 这里，其实 $(s_{tan},\dot{s}_{tan})$ 它自己也是一个从减速到加速的开关，把它当成s2，也加入到开关列表里面。

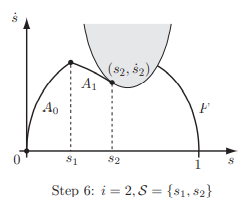
那么再从s2开始试着用U往前走，这次发现交到了F曲线，那么就又确定了加速到减速的开关：

那么通过这一系列的加速和减速切换开关，我们就能以最大的加速度和减速度，在满足机器人动力学约束的前提下，尽可能的完成轨迹生成，花费的时间T最小。

该算法假设三点：

1.保持静止状态，假设机器人可以在任意状态和重力对抗保持位形。

2.不容许状态，即低于速度极限约束的速度都是可以执行的，高于速度极限约束的速度都是不能执行的。

3.不存在零惯量点。（中文版211页，提到的“零惯量点”处印刷错误，写成了 $m_i(s)<0$ ,实际上英文版原文是：

那么如果这玩意是0，即存在零惯量点，那么扭矩不依赖于加速度，那么执行器就只有速度约束。这种情况下应该选择和速度极限曲线相切的加速度来保证时间最优。