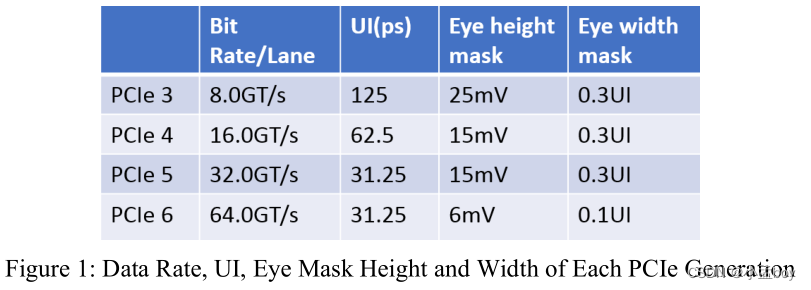
在高速SerDes传输系统中，随着信号速率的提高，UI会越来越小，传输线的对内skew会越来越大。以PCIe信号来说，PCIe4.0速率的一个UI是62.5ps，当速率提高到PCIe5.0时，每个UI就只有31.25ps，更进一步，当速率提高到PCIe6.0时，接收端的eye mask会更小。近几年，对内skew分析是一个比较热门的课题，PCB的玻纤效应是导致对内skew的一个重要因素。当传输线与working pannel的边缘平行时（意味着走线和经向或纬向平行），通常由于玻纤效应而导致对内skew。这种由玻纤效应导致的对内skew通常毫无规律，因此难以管控。缓解玻纤效应的一种有效方法是角度走线，目前已经广泛应用于高速PCB设计中。然而，在PCB的某些区域，例如breakout和breakin区域，角度走线并不现实，因此就必须管控非角度走线的总长度。

 玻纤模型

玻纤效应介绍

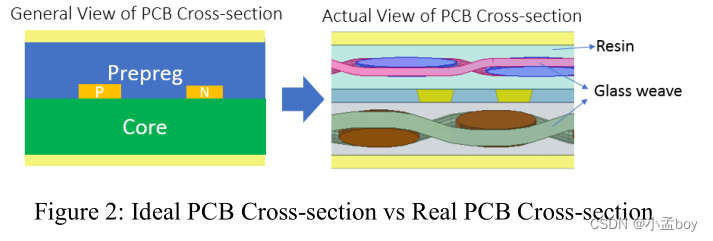
简化的PCB板材模型如下左图所示，走线被夹在core和pp中间，core和pp是各向同性的。但是实际的PCB介质是各向异性的，这是因为里面大部分由树脂和玻璃纤维组成，如下右图所示。

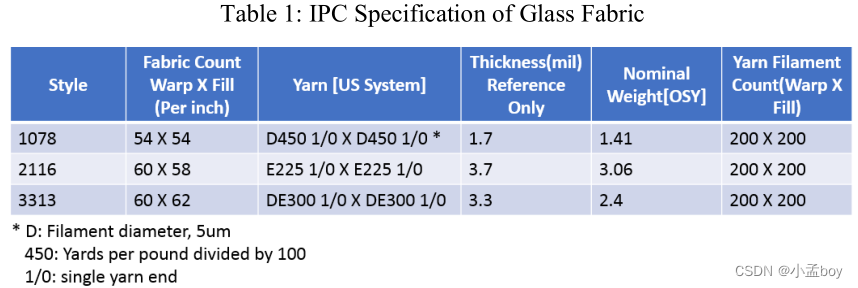
 平纹是电子行业最常用的玻纤编织风格。每个纹路包含经向和纬向，这种玻纤织物并不是紧密的排列，而是有很多空窗。经向和纬向的织物尺寸也不相同，因此，空窗的经向宽度和纬向长度也并不相同。IPC规范已经定义了不同玻纤规格中纱的规格和密度。以1078为例，经向和纬向有相同的织物数量，每inch有54跟织物。经向和纬向的织物包含相同的纱线。每个织物由200个直径5um的玻璃纱组成，因此也被称为正方形织物。

 

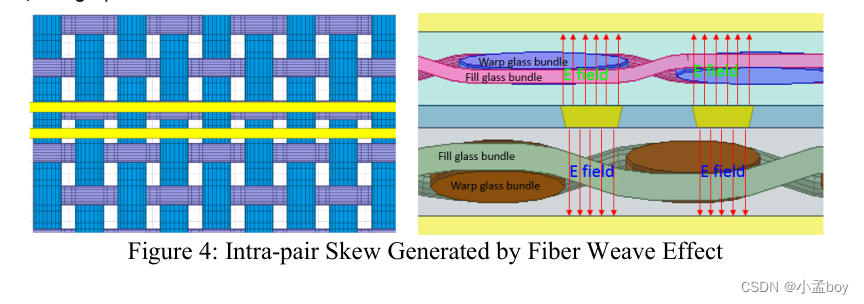
树脂和玻布的Dk差距非常大，E玻布 Dk大约6.8，low Dk的玻布大约4.8，而绝大多数的PCB中树脂的Dk在2.7-3.0。所以说，如果差分对中的一根线走在了玻纤束上，另一根走在了开窗位置，两个走线的电场会穿过不同的材料，相应的Dk值也不一样，就会观测到对内skew。玻布和树脂的Dk差距越大，对内skew也越大。

玻纤模型

以上分析可知，玻纤效应导致的对内skew直接受走线和玻纤的位置影响。但是在加工过程中，走线位置和玻纤的位置是不规律的，因此玻纤效应导致的skew也是无规律的。对内skew的总量和走线长度，走线宽度，玻纤开窗大小，走线间距，玻纤规格，走线角度，走线和玻纤位置等等都有关系。因此，玻纤效应导致的对内skew是一个非常复杂的统计问题。每一块PCB都由很多玻璃束组成，每个玻璃束又由很多玻璃丝组成。

 

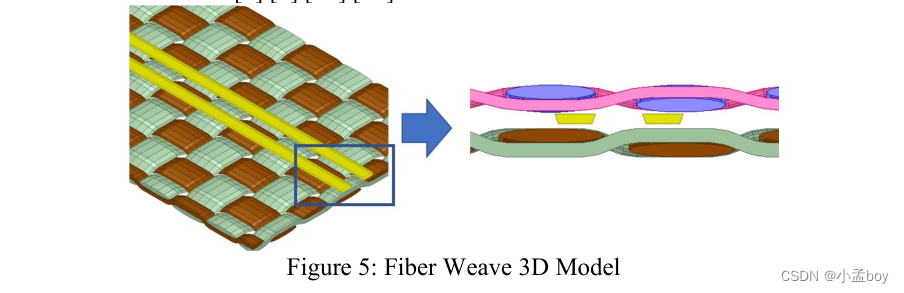
尽管模型被切成了很多小块，但是仍然不太可能用复杂的几何图形来仿真成千上万的玻璃丝。为了简化模型复杂性，包含成千上万的玻璃丝的玻璃束在仿真时将被看作一个实心的块，如上图所示，另外，玻璃束的横截面形状被视为椭圆。这样，模拟纤维编织的传统方法是将玻璃丝束建模为实心椭圆玻璃块。椭圆玻璃束的材质建模为纯玻璃。

但是这样仍然无法仿真一大块PCB，一般在仿真时，PCB被切成很多小块。然而，对内skew也和反射有关，为了最小化反射，可以级联很多个S参数，总长度达到约5inch，然后再计算对内skew。下面的公式展示了使用混合模式的S参数计算skew。

 

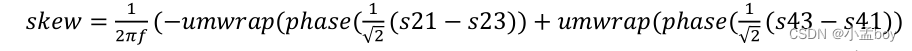
纤维编织是周期性的，但是core和pp的周期是不一样的，所以左侧模型的边缘选在了core玻璃束和pp玻璃束中间的位置，右侧边缘也是一样。因此，模型的左右两侧可以级联在一起。

下图展示了一个真实的PCB横截面，白点就是玻璃丝。首先，玻璃束的轮廓大约是椭圆形的。在轮廓内，白点并没有占据所有的空间，这就意味着在玻璃束的椭圆轮廓内，玻璃丝并没有紧密排列，玻璃束体积内的物体是玻璃丝和树脂的混合物，不是纯玻璃丝。 由于纯玻璃丝的Dk比玻璃丝和树脂混合物的Dk要大，所以仿真出来的传输线阻抗要比实际阻抗低。

上图中，目标实际阻抗是85Ohm，但是仿真结果比实际低了约6Ohm，这就是不正确地估计Dk导致的。考虑到玻璃束椭圆体积内有玻璃丝和树脂，如果需要建模非常精确的话，就需要给玻璃丝建模，这就太复杂了，所以比较实用的方法是找到一个玻璃丝和树脂混合物的有效Dk 。

本文章中，在玻璃束模型中使用有效Dk来取代纯玻璃丝Dk。有效Dk由玻璃Dk和树脂Dk以及相应的提及确定：

 

上式中，从左到右依次是有效Dk，玻璃丝体积，树脂体积，树脂Dk，玻璃丝Dk。由于树脂和玻璃丝的Dk已知，所以只需要知道玻璃束中玻璃丝和树脂所占的体积比就可以得到有效Dk。体积比又可以转换为横截面中玻璃丝和树脂所占区域的比值。在上文最开始的表1中，IPC定义了玻璃丝的直径和数量。那么在横截面中玻璃丝所占的区域就可以计算出来了。玻璃束的宽度和厚度可以测试玻布得出。这样，就可以算出玻璃束横截面积中玻璃丝和树脂所占的面积比例 。下表2展示了比较常见的玻布中玻璃丝和树脂的比例，可以看出几乎一半的体积被树脂占据。

下图展示了有效Dk随着玻璃体积比变化而变化。如果玻璃体积比例为0.55，树脂的Dk为2.8，那么E玻璃束的有效Dk为4.3，如果使用low Dk的玻璃，有效Dk会降低到约3.2。 

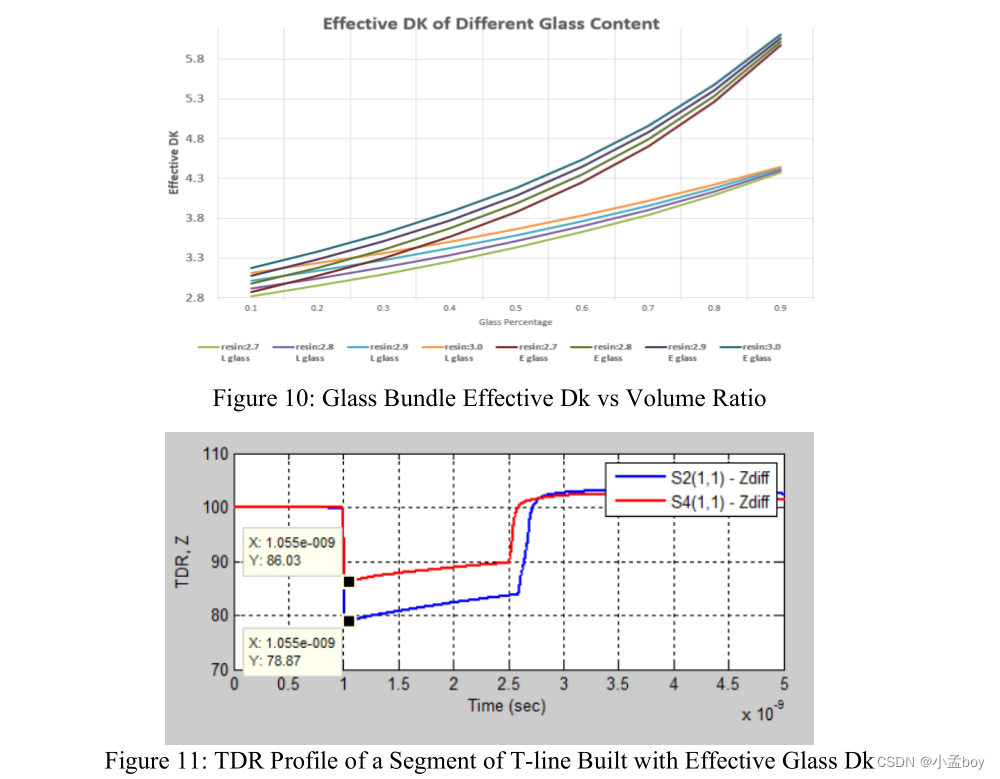
使用有效Dk重新建模得出的阻抗如上图的红线所示，更接近于85Ohm，所以在玻璃束中使用有效Dk是一个更合理的做法。