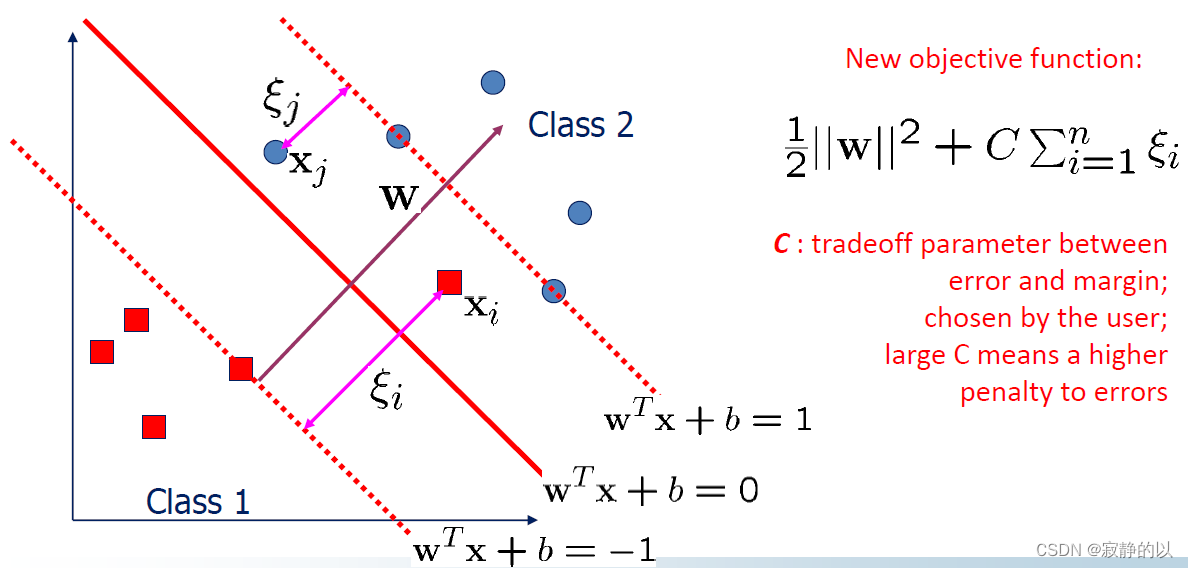
1、Soft Margin SVM 对偶求解
构造拉格朗日函数
L
=
1
2
∥
w
∥
2
+
C
∑
i
=
1
n
ξ
i
−
∑
i
=
1
n
α
i
(
y
i
(
w
T
x
i
+
b
)
−
1
+
ξ
i
)
−
∑
i
=
1
n
γ
i
ξ
i
α
i
≥
0
γ
i
≥
0
\begin{aligned} & L=\frac{1}{2}\|w\|^2+C \sum_{i=1}^n \xi_i-\sum_{i=1}^n \alpha_i\left(y_i\left(w^T x_i+b\right)-1+\xi_i\right)-\sum_{i=1}^n \gamma_i \xi_i \\ & \alpha_i \geq 0 \quad \gamma_i \geq 0 \end{aligned}
L=21∥w∥2+Ci=1∑nξi−i=1∑nαi(yi(wTxi+b)−1+ξi)−i=1∑nγiξiαi≥0γi≥0
求偏导
∂
L
∂
w
=
0
⇒
w
=
∑
i
α
i
y
i
x
i
∂
L
∂
b
=
0
⇒
∑
i
α
i
y
i
=
0
∂
L
∂
ξ
i
=
0
⇒
α
i
+
γ
i
=
C
⇒
0
≤
α
i
≤
C
\begin{gathered} \frac{\partial L}{\partial w}=0 \Rightarrow w=\sum_i \alpha_i y_i x_i \\ \frac{\partial L}{\partial b}=0 \Rightarrow \sum_i \alpha_i y_i=0 \\ \frac{\partial L}{\partial \xi_i}=0 \Rightarrow \alpha_i+\gamma_i=C \Rightarrow 0 \leq \alpha_i \leq C \end{gathered}
∂w∂L=0⇒w=i∑αiyixi∂b∂L=0⇒i∑αiyi=0∂ξi∂L=0⇒αi+γi=C⇒0≤αi≤C
于是问题转化为
max
.
W
(
α
)
=
∑
i
=
1
n
α
i
−
1
2
∑
i
=
1
,
j
=
1
n
α
i
α
j
y
i
y
j
x
i
T
x
j
subject to
C
≥
α
i
≥
0
,
∑
i
=
1
n
α
i
y
i
=
0
\begin{aligned} & \max . W(\boldsymbol{\alpha})=\sum_{i=1}^n \alpha_i-\frac{1}{2} \sum_{i=1, j=1}^n \alpha_i \alpha_j y_i y_j \mathbf{x}_i^T \mathbf{x}_j \\ & \text { subject to } C \geq \alpha_i \geq 0, \sum_{i=1}^n \alpha_i y_i=0 \end{aligned}
max.W(α)=i=1∑nαi−21i=1,j=1∑nαiαjyiyjxiTxj subject to C≥αi≥0,i=1∑nαiyi=0
并且注意到
w
=
∑
j
=
1
s
α
t
j
y
t
j
x
t
j
\mathbf{w}=\sum_{j=1}^s \alpha_{t_j} y_{t_j} \mathbf{x}_{t_j}
w=∑j=1sαtjytjxtj
- 在对偶空间中,Hard Margin SVM和Soft Margin SVM得到了统一,唯一不同就是这边的拉格朗日乘子 α i \alpha_i αi有一个上界 C C C
- 在对偶空间中,Soft Margin SVM也是一个QP问题!!!
KKT条件
{
α
i
(
y
i
f
(
x
i
)
−
1
+
ξ
i
)
=
0
γ
i
ξ
i
=
0
α
i
+
γ
i
=
C
⇒
0
≤
α
i
≤
C
\left\{\begin{array}{l} \alpha_i\left(y_i f\left(x_i\right)-1+\xi_i\right)=0 \\ \gamma_i \xi_i=0 \\ \alpha_i+\gamma_i=C \Rightarrow 0 \leq \alpha_i \leq C \end{array}\right.
⎩
⎨
⎧αi(yif(xi)−1+ξi)=0γiξi=0αi+γi=C⇒0≤αi≤C
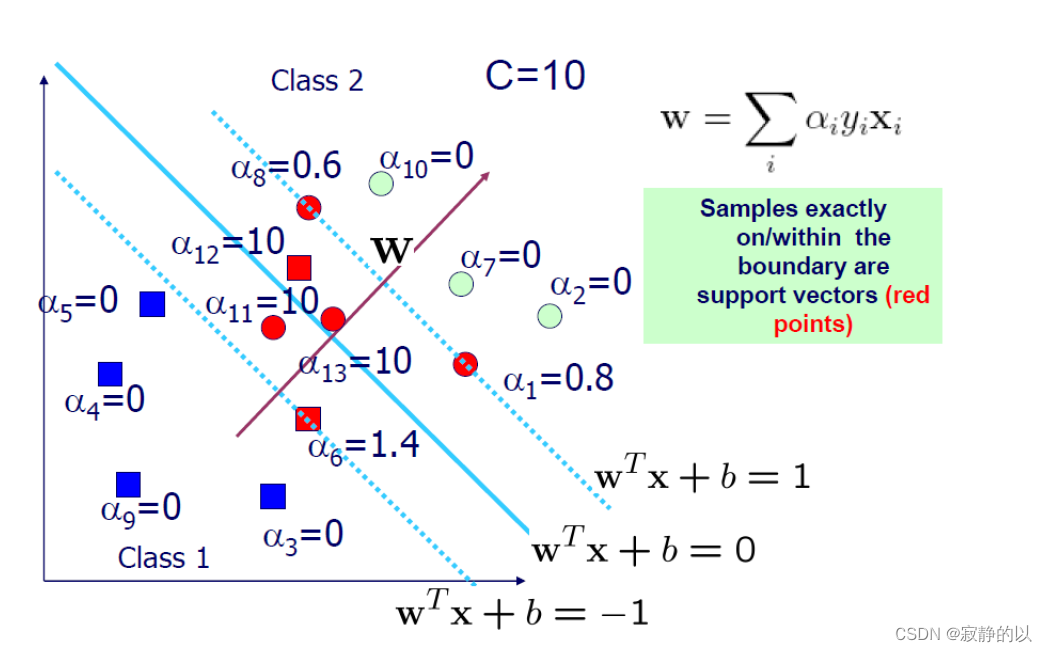
{
α
i
=
0
⇒
y
i
f
(
x
i
)
≥
1
⇒
Samples outside the boundary
0
<
α
i
<
C
⇒
y
i
f
(
x
i
)
=
1
⇒
Samples on the boundary
α
i
=
C
⇒
y
i
f
(
x
i
)
≤
1
⇒
Samples within the boundary
\begin{cases}\alpha_i=0 & \Rightarrow y_i f\left(x_i\right) \geq 1 \Rightarrow \text { Samples outside the boundary } \\ 0<\alpha_i<C & \Rightarrow y_i f\left(x_i\right)=1 \Rightarrow \text { Samples on the boundary } \\ \alpha_i=C & \Rightarrow y_i f\left(x_i\right) \leq 1 \Rightarrow \text { Samples within the boundary }\end{cases}
⎩
⎨
⎧αi=00<αi<Cαi=C⇒yif(xi)≥1⇒ Samples outside the boundary ⇒yif(xi)=1⇒ Samples on the boundary ⇒yif(xi)≤1⇒ Samples within the boundary
如何求偏置
b
b
b
0
<
α
i
<
C
⇒
y
i
f
(
x
i
)
=
1
f
(
z
)
=
∑
j
=
1
s
α
j
y
j
x
j
T
z
+
b
\begin{gathered} 0<\alpha_i<C \Rightarrow y_i f\left(\mathrm{x}_i\right)=1 \\ f(\mathrm{z})=\sum_{j=1}^s \alpha_j y_j \mathrm{x}_j^T \mathrm{z}+b \end{gathered}
0<αi<C⇒yif(xi)=1f(z)=j=1∑sαjyjxjTz+b
b
=
y
i
−
∑
j
=
1
s
α
j
y
j
x
j
T
x
i
∀
0
<
α
i
<
C
b=y_i-\sum_{j=1}^s \alpha_j y_j x_j^T x_i \quad \forall 0<\alpha_i<C
b=yi−j=1∑sαjyjxjTxi∀0<αi<C
随便找一个支撑向量点,带进去就能算出
b
b
b。不同的支撑向量点算出的
b
b
b是一样的。
2、非线性SVM
对于任意给定的线性不可分的数据集,我们总能找到一种映射 ϕ ( ⋅ ) \phi(\cdot) ϕ(⋅),在映射空间中,样本点是线性可分的。
回忆一下
maximize
∑
i
=
1
N
α
i
−
1
2
∑
i
=
j
=
1
N
α
i
α
j
y
i
y
j
x
i
x
j
subject to
C
≥
α
i
≥
0
,
∑
i
=
1
N
α
i
y
i
=
0
\begin{aligned} \text { maximize } & \sum_{i=1}^N \alpha_i-\frac{1}{2} \sum_{i=j=1}^N \alpha_i \alpha_j y_i y_j x_i x_j \\ \text { subject to } & C \geq \alpha_i \geq 0, \sum_{i=1}^N \alpha_i y_i=0 \end{aligned}
maximize subject to i=1∑Nαi−21i=j=1∑NαiαjyiyjxixjC≥αi≥0,i=1∑Nαiyi=0
我们发现,当把数据映射到高维空间后,我们只需要计算数据之间的内积,因此我们不去显式地去定义
ϕ
(
⋅
)
\phi(\cdot)
ϕ(⋅),转而去定义高维空间的内积,也就是核函数
K
(
x
i
,
x
j
)
=
ϕ
(
x
i
)
⋅
ϕ
(
x
j
)
K\left(x_i, x_j\right)=\phi\left(x_i\right) \cdot \phi\left(x_j\right)
K(xi,xj)=ϕ(xi)⋅ϕ(xj)
所以非线性SVM只要把所有的内积都换成核函数就行了
max
.
W
(
α
)
=
∑
i
=
1
n
α
i
−
1
2
∑
i
=
1
,
j
=
1
n
α
i
α
j
y
i
y
j
x
i
T
x
j
subject to
C
≥
α
i
≥
0
,
∑
i
=
1
n
α
i
y
i
=
0
\begin{aligned} & \max . W(\boldsymbol{\alpha})=\sum_{i=1}^n \alpha_i-\frac{1}{2} \sum_{i=1, j=1}^n \alpha_i \alpha_j y_i y_j \mathbf{x}_i^T \mathbf{x}_j \\ & \text { subject to } C \geq \alpha_i \geq 0, \sum_{i=1}^n \alpha_i y_i=0 \end{aligned}
max.W(α)=i=1∑nαi−21i=1,j=1∑nαiαjyiyjxiTxj subject to C≥αi≥0,i=1∑nαiyi=0
换成
max
.
W
(
α
)
=
∑
i
=
1
n
α
i
−
1
2
∑
i
=
1
,
j
=
1
n
α
i
α
j
y
i
y
j
K
(
x
i
,
x
j
)
subject to
C
≥
α
i
≥
0
,
∑
i
=
1
n
α
i
y
i
=
0
\begin{aligned} & \max . W(\boldsymbol{\alpha})=\sum_{i=1}^n \alpha_i-\frac{1}{2} \sum_{i=1, j=1}^n \alpha_i \alpha_j y_i y_j K\left(\mathbf{x}_i, \mathbf{x}_j\right) \\ & \text { subject to } C \geq \alpha_i \geq 0, \sum_{i=1}^n \alpha_i y_i=0 \end{aligned}
max.W(α)=i=1∑nαi−21i=1,j=1∑nαiαjyiyjK(xi,xj) subject to C≥αi≥0,i=1∑nαiyi=0
最终的分类器
w
=
∑
j
=
1
s
α
t
j
y
t
j
x
t
j
f
=
w
T
z
+
b
=
∑
j
=
1
s
α
t
j
y
t
j
x
t
j
T
z
+
b
\begin{aligned} & \mathbf{w}=\sum_{j=1}^s \alpha_{t_j} y_{t_j} \mathbf{x}_{t_j} \\ & f=\mathbf{w}^T \mathbf{z}+b=\sum_{j=1}^s \alpha_{t_j} y_{t_j} \mathbf{x}_{t_j}^T \mathbf{z}+b \end{aligned}
w=j=1∑sαtjytjxtjf=wTz+b=j=1∑sαtjytjxtjTz+b
换成
w
=
∑
j
=
1
s
α
t
j
y
t
j
ϕ
(
x
t
j
)
f
=
⟨
w
,
ϕ
(
z
)
⟩
+
b
=
∑
j
=
1
s
α
t
j
y
t
j
K
(
x
t
j
,
z
)
+
b
\begin{aligned} \mathbf{w} & =\sum_{j=1}^s \alpha_{t_j} y_{t_j} \phi\left(\mathbf{x}_{t_j}\right) \\ f & =\langle\mathbf{w}, \phi(\mathbf{z})\rangle+b=\sum_{j=1}^s \alpha_{t_j} y_{t_j} K\left(\mathbf{x}_{t_j}, \mathbf{z}\right)+b \end{aligned}
wf=j=1∑sαtjytjϕ(xtj)=⟨w,ϕ(z)⟩+b=j=1∑sαtjytjK(xtj,z)+b
可以看到,非线性SVM中,咱们构造不出
w
\mathbf{w}
w了,好在最终的判别函数要计算的还是内积,可以直接计算判别函数值,而不用去显式地把分类器表示出来。
最终的
b
b
b
b
=
y
i
−
∑
j
=
1
s
α
j
y
j
x
j
T
x
i
∀
0
<
α
i
<
C
b=y_i-\sum_{j=1}^s \alpha_j y_j x_j^T x_i \quad \forall 0<\alpha_i<C
b=yi−j=1∑sαjyjxjTxi∀0<αi<C
换成
b
=
y
i
−
∑
j
=
1
s
α
j
y
j
k
(
x
j
,
x
i
)
∀
0
<
α
i
<
C
b=y_i-\sum_{j=1}^s \alpha_j y_j k\left(x_j, x_i\right) \quad \forall 0<\alpha_i<C
b=yi−j=1∑sαjyjk(xj,xi)∀0<αi<C
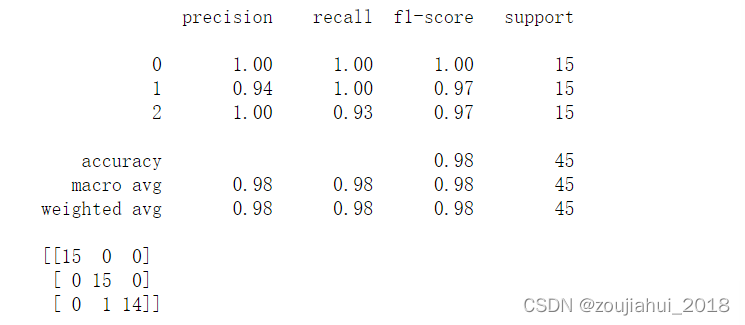
3、An Example


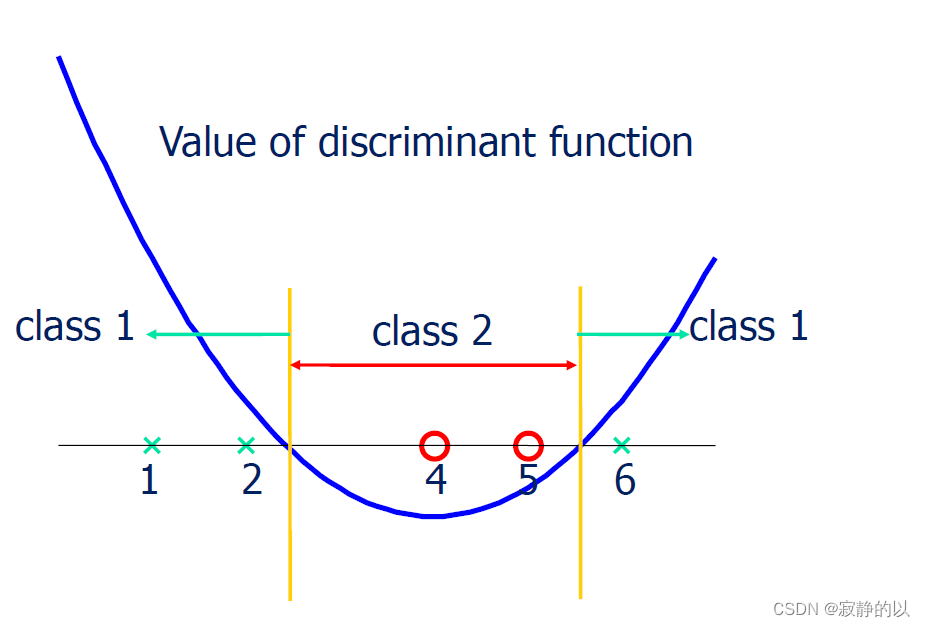
4、SVM是凸优化
回忆一下凸函数
D
−
D-
D− a domain in
R
n
\mathbb{R}^n
Rn
f
(
(
1
−
α
)
x
0
+
α
x
1
)
≤
(
1
−
α
)
f
(
x
0
)
+
α
f
(
x
1
)
f\left((1-\alpha) \mathbf{x}_0+\alpha \mathbf{x}_1\right) \leq(1-\alpha) f\left(\mathbf{x}_0\right)+\alpha f\left(\mathbf{x}_1\right)
f((1−α)x0+αx1)≤(1−α)f(x0)+αf(x1)
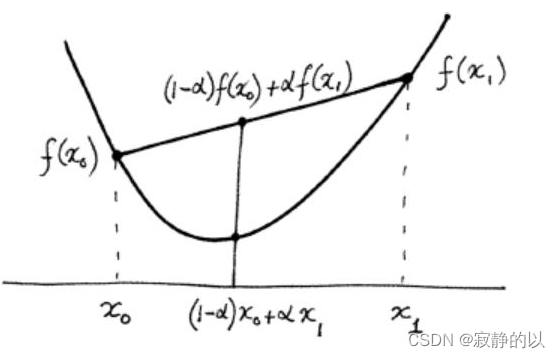
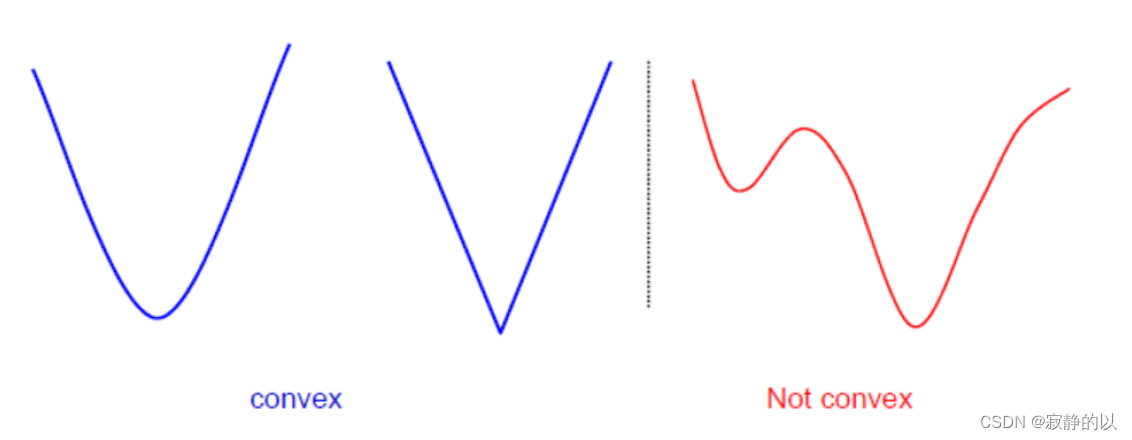
SVM的优化问题是
min
w
∈
R
d
C
∑
i
N
max
(
0
,
1
−
y
i
f
(
x
i
)
)
+
∥
w
∥
2
\min _{\mathbf{w} \in \mathbb{R}^d} C \sum_i^N \max \left(0,1-y_i f\left(\mathbf{x}_i\right)\right)+\|\mathbf{w}\|^2
w∈RdminCi∑Nmax(0,1−yif(xi))+∥w∥2
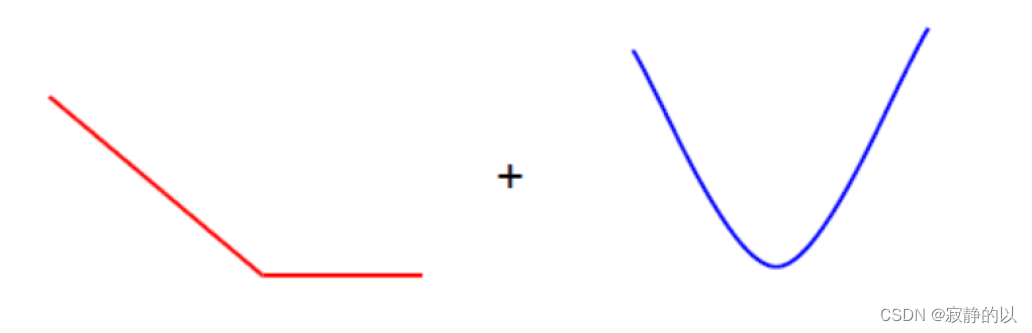
该式左半部分是Hinge Loss的和,右边是一个二次函数,由于凸函数的非负线性组合还是凸函数,所以SVM是个凸优化问题,也就是说,损失函数的 local minimum 就是 global minimum.







![[思考进阶]04 优秀的人,都在使用“微习惯”](https://img-blog.csdnimg.cn/51577adbd62244eb88926d9c0d294c61.png#pic_center)

![#P13787. [NOIP2021] 报数](https://img-blog.csdnimg.cn/82b3906bd9ca4937910d512017bb5b38.png)