介绍

sklearn 是 scikit–learn 的简称,是一个基于 Python 的第三方模块。
sklearn 库集成了一些常用的机器学习方法,在进行机器学习任务时,并不需要实现算法,只需要简单的调用 sklearn 库中提供的模块就能完成大多数的机器学习任务。

在sklearn中，一共有3个朴素贝叶斯的分类算法类：
GaussianNB（先验是高斯分布的朴素贝叶斯）；
BernoulliNB（先验为伯努利分布的朴素贝叶斯）；
MultinomialNB（先验是多项式分布的朴素贝叶斯）。
高斯NB用于连续值；多项式NB用于离散的多值；伯努利NB用于离散的二值。

高斯朴素贝叶斯则常用于连续特征的情况下。高斯朴素贝叶斯假设特征满足高斯分布（正态分布）。如特征为“某地高中生的身高”时，就使用高斯朴素贝叶斯。

实例化模型对象的时候，不需要对高斯朴素贝叶斯类输入任何的参数，可以说是一个非常轻量级的类，操作非常容易。
但过于简单也意味着贝叶斯没有太多的参数可以调整，因此贝叶斯算法的成长空间并不是太大，如果贝叶斯算法的效果不是太理想，我们一般都会考虑换模型。

GaussianNB()参数介绍

  GaussianNB(*, priors=None, var_smoothing=1e-09)

参数:

priors : array-like of shape (n_classes,),Prior probabilities of the classes. If specified the priors are not adjusted according to the data.
先验：数组-（n_classes,）每一类的先验概率。如果指定先验概率，则不会根据数据调整先验概率。
var_smoothing : float, default=1e-9
方差平滑：浮点数，默认=1e-9，为了计算稳定性而添加到方差中的所有特征的最大方差部分。

属性：

类别数 class_count_：ndarray of shape (n_classes,)，在每个类中观察到的训练样本数。
类别先验概率 class_prior_：ndarray of shape (n_classes,)，每个类别的先验概率。
类标签 classes_：ndarray of shape (n_classes,)，分类器已知的类标签。
epsilon_：浮点数，方差的绝对附加值。
sigma_ : ndarray of shape (n_classes, n_features)，每类每个特征的方差
theta_ : ndarray of shape (n_classes, n_features)，每类每个特征的平均值

实例

#导入鸢尾花数据集
from sklearn.datasets import load_iris #sklearn内置数据集sklearn
from sklearn import model_selection #拆分数据集【训练集测试集】
from sklearn.naive_bayes import GaussianNB #导入先验是高斯分布的朴素贝叶斯模型

iris=load_iris()
x=iris.data
y=iris.target
x_train,x_test,y_train,y_test=model_selection.train_test_split(x,y,test_size=0.3,random_state=123456) #random_state控制随机状态。


model=GaussianNB()  #模型为先验是高斯分布的朴素贝叶斯
model.fit(x_train,y_train) #拟合训练
predict=model.predict(x_test) #预测

from sklearn import metrics
from sklearn.metrics import classification_report 
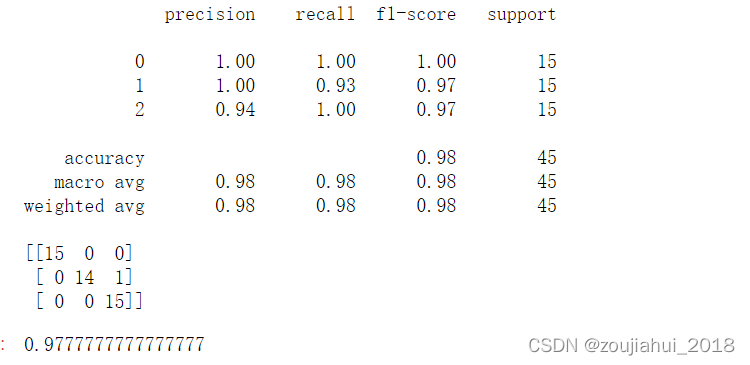
print(classification_report(y_test,predict)) 
print(metrics.confusion_matrix(y_test, predict))#混淆矩阵
model.score(x_test,y_test)

# 混淆矩阵要表达的含义：

# 1、混淆矩阵的每一列代表了预测类别，每一列的总数表示预测为该类别的数据的数目；
# 2、每一行代表了数据的真实归属类别，每一行的数据总数表示该类别的数据实例的数目；每一列中的数值表示真实数据被预测为该类的数目。
# True Positive（TP）：真正类。样本的真实类别是正类，并且模型识别的结果也是正类。
# False Negative（FN）：假负类。样本的真实类别是正类，但是模型将其识别为负类。
# False Positive（FP）：假正类。样本的真实类别是负类，但是模型将其识别为正类。
# True Negative（TN）：真负类。样本的真实类别是负类，并且模型将其识别为负类。

在这里插入图片描述

BernoulliNB()参数介绍

BernoulliNB(*, alpha=1.0, binarize=1, fit_prior=True, class_prior=None)

参数:

alpha : float, default=1.0
浮点数，平滑参数（0表示无平滑）。
binarize : float or None, default=0.0
二进制化：浮点或无，默认值=0.0，样本特征二值化（映射到布尔值）的阈值。如果为“无”，则假定输入已由二进制矢量组成。
binarize：将数据特征二值化的阈值，大于此阈值为1，小于此阈值为0，（就多了一个参数，其他参数与多项式朴素贝叶斯相同）
BernoulliNB实现了用于多元Bernoulli分布数据的朴素Bayes训练和分类算法；即，可能有多个特征，但每个特征都假定为二值（Bernoulli，boolean）变量。因此，此类算法要求样本以二值特征向量表示；如果传递任何其他类型的数据，BernoulliNB实例可以对其输入进行二值化（取决于binarize 参数）。
fit_prior : bool, default=True
是否学习类先验概率。如果为假，将使用统一的先验。
class_prior : array-like of shape (n_classes,), default=None
类的先验概率。如果指定，则不根据数据调整先验。

属性:

class_count_ : ndarray of shape (n_classes)
拟合时每个类的样本数。该值由样本权重（当提供时）加权。
训练样本中各类别对应的样本数，按类的顺序排序输出
class_log_prior_ : ndarray of shape (n_classes)
每个类的对数概率（平滑）各类标记的平滑先验概率对数值，其取值会受fit_prior和class_prior参数的影响
classes_ : ndarray of shape (n_classes,)
分类器已知的类标签
feature_count_ : ndarray of shape (n_classes, n_features)
拟合时每个（类、特征）的样本数。该值由样本权重（当提供时）加权。
各类别各个特征出现的次数，返回形状为(n_classes, n_features)数组
feature_log_prob_ : ndarray of shape (n_classes, n_features)
给定类的特征的经验对数概率
给出一个类的特征条件概率P(xi | y)的对数值，返回形状为(n_classes, n_features)数组
coef_ : ndarray of shape (n_classes, n_features) 系数
intercept_ : ndarray of shape (n_classes,) 截距
n_features_ : int
整数每个样本的特征数量。

实例

#例子

import numpy as np
from sklearn.datasets import make_blobs
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import BernoulliNB  # 伯努利贝叶斯: 专门用于处理（多元）二项分布
from sklearn.metrics import brier_score_loss  # 布里尔分数


class_1_samples = 500
class_2_samples = 500
centers = [[0.0, 0.0], [2.0, 2.0]]  # (1000,2)  ==>  centers = [[0.0, 0.0, 0.0], [2.0, 2.0, 2.0]] (1000, 3)
cluster_std = [0.5, 0.5]
X, y = make_blobs(n_samples=[class_1_samples, class_2_samples], centers=centers, cluster_std=cluster_std, random_state=42, shuffle=False)
print(X.shape)  # [1000, 2]
print(np.unique)  # array([0, 1])

Xtrain, Xtest, ytrain, ytest = train_test_split(X, y, test_size=0.3, random_state=42)
print(Xtrain)#非二值化 变量特征们

mms = MinMaxScaler().fit(Xtrain)
Xtrain = mms.transform(Xtrain)
Xtest = mms.transform(Xtest)

bnl_ = BernoulliNB()
bnl_.fit(Xtrain, ytrain)  # 不设置二值化

print("不进行二值化的模型得分：")
print(bnl_.score(Xtest, ytest))

bnl = BernoulliNB(binarize=0.5) # 设置二值化阈值为0.5，将特征二值化【特征大于0.5，则为1；特征小于0.5，则为0  二值化处理结束】
bnl.fit(Xtrain, ytrain) 
print("二值化后的模型得分：")
print(bnl.score(Xtest, ytest))

brier_score_loss(ytest, bnl.predict_proba(Xtest)[:, 1], pos_label=1)

在这里插入图片描述

MultinomialNB()参数介绍

MultinomialNB(*, alpha=1.0, fit_prior=True, class_prior=None)

多项式朴素贝叶斯分类器适用于具有离散特征的分类（例如，文本分类中的字数）。
多项式分布通常需要整数特征计数。然而，在实践中，分数计数（如tf-idf）也可以。

参数

alpha : float, default=1.0
浮点数，平滑参数（0表示无平滑）
平滑先验𝛼≥0,让学习样本中不存在的特征占一定的比例，并防止在进一步的计算中出现零概率。𝛼=1 时为拉普拉斯(Laplace)平滑，𝛼<1时为李德斯通(Lidstone)平滑。
fit_prior : bool, default=True
是否学习类先验概率。如果为假，将使用统一的先验。
class_prior : array-like of shape (n_classes,), default=None
类的先验概率。如果指定，则不根据数据调整先验。

属性（和伯努利一样的）

class_count_ : ndarray of shape (n_classes)
拟合时每个类的样本数。该值由样本权重（当提供时）加权。
class_log_prior_ : ndarray of shape (n_classes)
每个类的对数概率（平滑）
classes_ : ndarray of shape (n_classes,)
分类器已知的类标签
coef_ : ndarray of shape (n_classes, n_features) 系数
feature_count_ : ndarray of shape (n_classes, n_features)
拟合时每个（类、特征）的样本数。该值由样本权重（当提供时）加权。
feature_log_prob_ : ndarray of shape (n_classes, n_features)
给定类的特征的经验对数概率
intercept_ : ndarray of shape (n_classes,) 截距
n_features_ : int
整数每个样本的特征数量

实例

#离散情况 多项式贝叶斯
import numpy as np
from sklearn.datasets import make_blobs
from sklearn.preprocessing import KBinsDiscretizer  # 离散化
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import brier_score_loss  # 布里尔分数 : for bin_class


class_1_samples = 400
class_2_samples = 400
centers = [[0.0, 0.0], [2.0, 2.0]]  # (800,2) 
cluster_std = [0.5, 0.5]
X, y = make_blobs(n_samples=[class_1_samples, class_2_samples], centers=centers, cluster_std=cluster_std, random_state=42, shuffle=False)
print(X.shape)  # [800, 2]
print(np.unique)  # array([0, 1])

Xtrain, Xtest, ytrain, ytest = train_test_split(X, y, test_size=0.3, random_state=42)


###使用KBinsDiscretizer离散化连续特征
kbs = KBinsDiscretizer(n_bins=10, encode="onehot")
kbs.fit(Xtrain)
Xtrain_ = kbs.transform(Xtrain)
Xtest_ = kbs.transform(Xtest)
print(Xtrain_.shape)  


mnb = MultinomialNB()
mnb.fit(Xtrain_, ytrain)
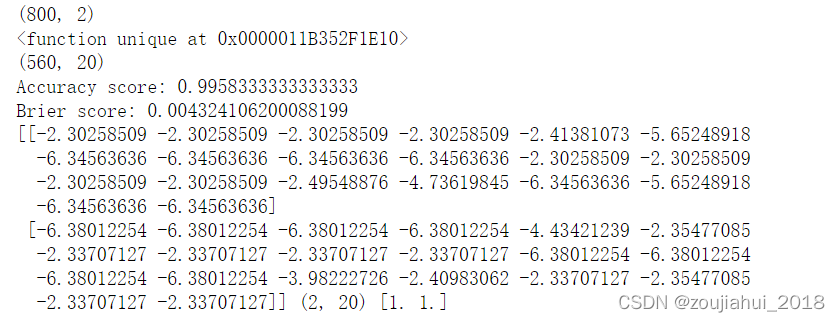
print("Accuracy score:", mnb.score(Xtest_, ytest))
print("Brier score:", brier_score_loss(ytest, mnb.predict_proba(Xtest_)[:, 1], pos_label=1))# 越接近 0 越好;
print(mnb.feature_log_prob_, mnb.feature_log_prob_.shape, np.exp(mnb.feature_log_prob_).sum(1))  # 一个固定标签类别下的每个特征的对数概率

在这里插入图片描述

#导入鸢尾花数据集
from sklearn.datasets import load_iris #sklearn内置数据集sklearn
iris=load_iris()
x=iris.data
y=iris.target
from sklearn import model_selection #拆分数据集【训练集测试集】
x_train,x_test,y_train,y_test=model_selection.train_test_split(x,y,test_size=0.3,random_state=123456) 
model=MultinomialNB()  #模型为先验是多项式分布的朴素贝叶斯
model.fit(x_train,y_train) #拟合训练
predict=model.predict(x_test) #预测

from sklearn import metrics
from sklearn.metrics import classification_report 
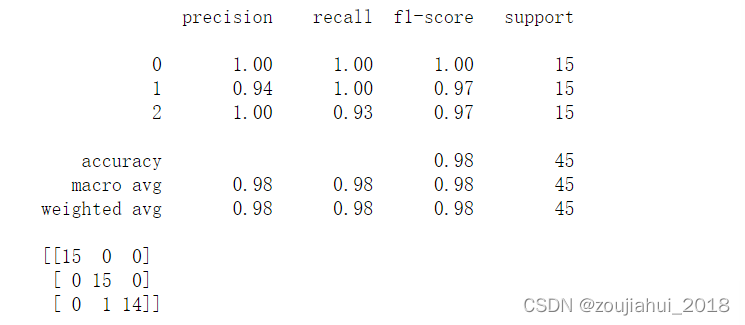
print(classification_report(y_test,predict)) 
print(metrics.confusion_matrix(y_test, predict))