文章目录
- 内积空间
- 1 内积空间
- 2 标准正交向量集
- 3 Gram-Schmidt正交化方法
- 4 正交子空间
- 5 最小二乘问题
- 6 正交矩阵和酉矩阵
内积空间
1 内积空间
-
内积空间定义
设 V V V是在数域 F F F上的向量空间,则 V V V到 F F F的一个代数运算记为 ( α , β ) (\alpha,\beta) (α,β)。如果 ( α , β ) (\alpha,\beta) (α,β)满足以下条件:
- ( α , β ) = ( β , α ) ‾ (\alpha,\beta)=\overline{(\beta,\alpha)} (α,β)=(β,α)( ‾ \overline{} 表示共轭符,针对复数域,为了保证复数运算的正确性)
- ( α + β , γ ) = ( α , γ ) + ( β , γ ) (\alpha+\beta,\gamma)=(\alpha,\gamma)+(\beta,\gamma) (α+β,γ)=(α,γ)+(β,γ)
- ( k α , β ) = k ( α , β ) (k\alpha,\beta)=k(\alpha,\beta) (kα,β)=k(α,β)
- ( α , α ) ≥ 0 (\alpha,\alpha)\geq 0 (α,α)≥0,当且仅当 α = 0 \alpha=0 α=0时, ( α , α ) = 0 (\alpha,\alpha)=0 (α,α)=0。
其中 k ∈ F , α , β , γ ∈ V k\in F,\alpha,\beta,\gamma\in V k∈F,α,β,γ∈V。则称 ( α , β ) (\alpha,\beta) (α,β)为 α \alpha α和 β \beta β的内积。定义了内积的向量空间 V V V称为内积空间。特别地,称实数域 R R R上的内积空间 V V V为Euclid空间(欧式空间);称复数域 C C C上的内积空间 V V V为酉空间。
-
标准内积
-
在实数域 R R R上的 n n n维向量空间 R n R^n Rn中,对向量 x = ( x 1 , ⋯ , x n ) T , y = ( y 1 , ⋯ , y n ) T x=(x_1,\cdots,x_n)^T,y=(y_1,\cdots,y_n)^T x=(x1,⋯,xn)T,y=(y1,⋯,yn)T,定义内积
( x , y ) = y T x = ( y 1 ⋯ y n ) ( x 1 ⋮ x n ) = ∑ i = 1 n x i y i (x,y)=y^Tx=\begin{pmatrix}y_1&\cdots &y_n\end{pmatrix}\begin{pmatrix}x_1\\ \vdots \\ x_n\end{pmatrix}=\sum_{\\i=1}^nx_iy_i (x,y)=yTx=(y1⋯yn) x1⋮xn =i=1∑nxiyi -
在复数域 C C C上的 n n n维向量空间 C n C^n Cn,对向量 x = ( x 1 , ⋯ , x n ) T , y = ( y 1 , ⋯ , y n ) T x=(x_1,\cdots,x_n)^T,y=(y_1,\cdots,y_n)^T x=(x1,⋯,xn)T,y=(y1,⋯,yn)T,定义内积
( x , y ) = y H x = ( y 1 ˉ ⋯ y n ˉ ) ( x 1 ⋮ x n ) = ∑ i = 1 n x i y i ˉ (x,y)=y^Hx=\begin{pmatrix}\bar{y_1}&\cdots &\bar{y_n}\end{pmatrix}\begin{pmatrix}x_1\\ \vdots \\ x_n\end{pmatrix}=\sum_{\\i=1}^nx_i\bar{y_i} (x,y)=yHx=(y1ˉ⋯ynˉ) x1⋮xn =i=1∑nxiyiˉ
其中 y H y^H yH表示 y y y的共轭转置。
以上两个内积我们称为 R n R^n Rn或 C n C^n Cn的标准内积,一般我们探讨的也就是标准内积。
-
-
重要定义
设 u , v u,v u,v是内积空间 V V V的向量
- 则 v v v的长度或范数为: ∣ ∣ v ∣ ∣ = ( v , v ) ||v||=\sqrt{(v,v)} ∣∣v∣∣=(v,v),长度为 1 1 1的称为单位向量。如果 v ≠ 0 v\neq 0 v=0,则 v ∣ ∣ v ∣ ∣ \frac{v}{||v||} ∣∣v∣∣v是一个单位向量
- 如果 v ≠ 0 v\neq 0 v=0,则 u u u在 v v v上的数量投影被定义为: α = ( u , v ) ∣ ∣ v ∣ ∣ \alpha=\frac{(u,v)}{||v||} α=∣∣v∣∣(u,v), u u u在 v v v上的向量投影被定义为: p = α v ∣ ∣ v ∣ ∣ = ( u , v ) ( v , v ) v p=\alpha\frac{v}{||v||}=\frac{(u,v)}{(v,v)}v p=α∣∣v∣∣v=(v,v)(u,v)v
- 如果 ( u , v ) = 0 (u,v)=0 (u,v)=0,则称 u u u和 v v v正交
-
内积的基本性质
设 u , v ∈ V u,v\in V u,v∈V,其中 V V V是内积空间,则
-
勾股定理:如果 u ⊥ v u\perp v u⊥v,则 ∣ ∣ u − v ∣ ∣ 2 = ∣ ∣ u ∣ ∣ 2 + ∣ ∣ v ∣ ∣ 2 ||u-v||^2=||u||^2+||v||^2 ∣∣u−v∣∣2=∣∣u∣∣2+∣∣v∣∣2
证明:
∣ ∣ u − v ∣ ∣ 2 = ( u − v , u − v ) = ( u , u − v ) + ( − v , u − v ) = ( u , u ) − ( u , v ) − ( v , u ) + ( v , v ) = ( u , u ) − ( u , v ) − ( u , v ) ‾ + ( v , v ) ||u-v||^2=(u-v,u-v)=(u,u-v)+(-v,u-v)\\=(u,u)-(u,v)-(v,u)+(v,v)=(u,u)-(u,v)-\overline{(u,v)}+(v,v) ∣∣u−v∣∣2=(u−v,u−v)=(u,u−v)+(−v,u−v)=(u,u)−(u,v)−(v,u)+(v,v)=(u,u)−(u,v)−(u,v)+(v,v)
-
柯西不等式: ∣ ( u , v ) ∣ ≤ ∣ ∣ u ∣ ∣ ∣ ∣ v ∣ ∣ |(u,v)|\leq ||u||\space ||v|| ∣(u,v)∣≤∣∣u∣∣ ∣∣v∣∣。等式成立当且仅当 u u u和 v v v线性相关。
证明:
如果 u , v u,v u,v线性相关,则设 u = k v , k ∈ F u=kv,k\in F u=kv,k∈F,则 ( u , v ) = ( k v , v ) = k ∣ ∣ v ∣ ∣ 2 (u,v)=(kv,v)=k||v||^2 (u,v)=(kv,v)=k∣∣v∣∣2
如果 u , v u,v u,v线性无关,设 z = u − ( u , v ) ( v , v ) v z=u-\frac{(u,v)}{(v,v)}v z=u−(v,v)(u,v)v,则 ( z , v ) = ( u − ( u , v ) ( v , v ) v , v ) = ( u , v ) − ( u , v ) ( v , v ) ( v , v ) = 0 (z,v)=(u-\frac{(u,v)}{(v,v)}v,v)=(u,v)-\frac{(u,v)}{(v,v)}(v,v)=0 (z,v)=(u−(v,v)(u,v)v,v)=(u,v)−(v,v)(u,v)(v,v)=0,则 z z z和 v v v正交。转换得到 u = z + ( u , v ) ( v , v ) v u=z+\frac{(u,v)}{(v,v)}v u=z+(v,v)(u,v)v,根据正交性,结合勾股定理则 ∣ ∣ u ∣ ∣ 2 = ∣ ∣ z ∣ ∣ 2 + ∣ ( u , v ) ( v , v ) ∣ 2 ∣ ∣ v ∣ ∣ 2 = ∣ ∣ z ∣ ∣ 2 + ∣ ( u , v ) ∣ 2 ( ∣ ∣ v ∣ ∣ 2 ) 2 ∣ ∣ v ∣ ∣ 2 = ∣ ∣ z ∣ ∣ 2 + ∣ ( u , v ) ∣ 2 ∣ ∣ v ∣ ∣ 2 ||u||^2=||z||^2+|\frac{(u,v)}{(v,v)}|^2||v||^2=||z||^2+\frac{|(u,v)|^2}{(||v||^2)^2}||v||^2=||z||^2+\frac{|(u,v)|^2}{||v||^2} ∣∣u∣∣2=∣∣z∣∣2+∣(v,v)(u,v)∣2∣∣v∣∣2=∣∣z∣∣2+(∣∣v∣∣2)2∣(u,v)∣2∣∣v∣∣2=∣∣z∣∣2+∣∣v∣∣2∣(u,v)∣2
又因为 ∣ ∣ z ∣ ∣ 2 > 0 ||z||^2> 0 ∣∣z∣∣2>0(线性无关, ∣ ∣ z ∣ ∣ 2 ||z||^2 ∣∣z∣∣2必大于 0 0 0),则 ∣ ( u , v ∣ < ∣ ∣ u ∣ ∣ ∣ ∣ v ∣ ∣ |(u,v|<||u||\space ||v|| ∣(u,v∣<∣∣u∣∣ ∣∣v∣∣
-
三角不等式: ∣ ∣ u + v ∣ ∣ 2 ≤ ∣ ∣ u ∣ ∣ 2 + ∣ ∣ v ∣ ∣ 2 ||u+v||^2\leq ||u||^2+||v||^2 ∣∣u+v∣∣2≤∣∣u∣∣2+∣∣v∣∣2
证明:
∣ ∣ u + v ∣ ∣ 2 = ( u + v , u + v ) = ( u , u + v ) + ( v , u + v ) = ( u , u ) + ( u , v ) + ( v , u ) + ( v , v ) = ( u , u ) + ( u , v ) + ( u , v ) ‾ + ( v , v ) ≤ ∣ ∣ u ∣ ∣ 2 + 2 ∣ ( u , v ) ∣ + ∣ ∣ v ∣ ∣ 2 ≤ ∣ ∣ u ∣ ∣ 2 + 2 ∣ ∣ u ∣ ∣ ∣ ∣ v ∣ ∣ + ∣ ∣ v ∣ ∣ 2 = ( ∣ ∣ u ∣ ∣ + ∣ ∣ v ∣ ∣ ) 2 ||u+v||^2=(u+v,u+v)=(u,u+v)+(v,u+v)\\=(u,u)+(u,v)+(v,u)+(v,v)=(u,u)+(u,v)+\overline{(u,v)}+(v,v)\\ \leq ||u||^2+2|(u,v)|+||v||^2 \leq ||u||^2+2||u||\space ||v||+||v||^2=(||u||+||v||)^2 ∣∣u+v∣∣2=(u+v,u+v)=(u,u+v)+(v,u+v)=(u,u)+(u,v)+(v,u)+(v,v)=(u,u)+(u,v)+(u,v)+(v,v)≤∣∣u∣∣2+2∣(u,v)∣+∣∣v∣∣2≤∣∣u∣∣2+2∣∣u∣∣ ∣∣v∣∣+∣∣v∣∣2=(∣∣u∣∣+∣∣v∣∣)2 -
平行四边形准则: ∣ ∣ u + v ∣ ∣ 2 + ∣ ∣ u − v ∣ ∣ 2 = 2 ( ∣ ∣ u ∣ ∣ 2 + ∣ ∣ v ∣ ∣ 2 ) ||u+v||^2+||u-v||^2=2(||u||^2+||v||^2) ∣∣u+v∣∣2+∣∣u−v∣∣2=2(∣∣u∣∣2+∣∣v∣∣2)
证明:
∣ ∣ u − v ∣ ∣ 2 = ( u − v , u − v ) = ( u , u − v ) + ( − v , u − v ) = ( u , u ) − ( u , v ) − ( v , u ) + ( v , v ) = ( u , u ) − ( u , v ) − ( u , v ) ‾ + ( v , v ) ∣ ∣ u + v ∣ ∣ 2 = ( u + v , u + v ) = ( u , u + v ) + ( v , u + v ) = ( u , u ) + ( u , v ) + ( v , u ) + ( v , v ) = ( u , u ) + ( u , v ) + ( u , v ) ‾ + ( v , v ) ∣ ∣ u + v ∣ ∣ 2 + ∣ ∣ u − v ∣ ∣ 2 = 2 ( u , u ) + 2 ( v , v ) = 2 ( ∣ ∣ u ∣ ∣ 2 + ∣ ∣ v ∣ ∣ 2 ) ||u-v||^2=(u-v,u-v)=(u,u-v)+(-v,u-v)\\=(u,u)-(u,v)-(v,u)+(v,v)=(u,u)-(u,v)-\overline{(u,v)}+(v,v)\\ ||u+v||^2=(u+v,u+v)=(u,u+v)+(v,u+v)\\=(u,u)+(u,v)+(v,u)+(v,v)=(u,u)+(u,v)+\overline{(u,v)}+(v,v)\\ ||u+v||^2+||u-v||^2=2(u,u)+2(v,v)=2(||u||^2+||v||^2) ∣∣u−v∣∣2=(u−v,u−v)=(u,u−v)+(−v,u−v)=(u,u)−(u,v)−(v,u)+(v,v)=(u,u)−(u,v)−(u,v)+(v,v)∣∣u+v∣∣2=(u+v,u+v)=(u,u+v)+(v,u+v)=(u,u)+(u,v)+(v,u)+(v,v)=(u,u)+(u,v)+(u,v)+(v,v)∣∣u+v∣∣2+∣∣u−v∣∣2=2(u,u)+2(v,v)=2(∣∣u∣∣2+∣∣v∣∣2)
-
2 标准正交向量集
-
正交向量集定义
设 v 1 , ⋯ , v n v_1,\cdots,v_n v1,⋯,vn是内积空间 V V V中的非零向量,如果 V V V中的任意两个向量 ( v i , v j ) = 0 ( i ≠ j ) (v_i,v_j)=0(i\neq j) (vi,vj)=0(i=j),则 V V V是一个正交向量集。
-
标准正交向量集定义
如果 V V V是一个正交向量集,且 V V V中的所有向量都是单位向量,即 ( v i , v i ) = 1 (v_i,v_i)=1 (vi,vi)=1,则 V V V是一个标准正交向量集。
-
正交向量集性质
如果 v 1 , ⋯ , v n v_1,\cdots,v_n v1,⋯,vn是内积空间 V V V的一个正交向量集,则 v 1 , ⋯ , v n v_1,\cdots,v_n v1,⋯,vn都是线性无关的。
-
正交基和标准正交基
在 n n n维内积空间中,由 n n n个正交向量组成的基称为正交基,由 n n n个标准正交向量组成的基称为标准正交基。
-
标准正交基表示向量坐标
设 u 1 , ⋯ , u n u_1,\cdots,u_n u1,⋯,un是内积空间 V V V的一个标准正交基,如果 v = ∑ i = 1 n c i u i v=\sum_{\\i=1}^nc_iu_i v=∑i=1nciui,则 c i = ( v , u i ) c_i=(v,u_i) ci=(v,ui)其中 c i c_i ci为向量 v v v在向量 u i u_i ui的标量投影。
-
Parseval公式
设 u 1 , ⋯ , u n u_1,\cdots,u_n u1,⋯,un是内积空间 V V V的一个标准正交基,如果 u = ∑ i = 1 n a i u i , v = ∑ i = 1 n b i u i u=\sum_{\\i=1}^na_iu_i,v=\sum_{\\i=1}^nb_iu_i u=∑i=1naiui,v=∑i=1nbiui,则 ( u , v ) = ∑ i = 1 n a i b i ˉ (u,v)=\sum_{\\i=1}^na_i\bar{b_i} (u,v)=∑i=1naibiˉ。并且, ∣ ∣ v ∣ ∣ 2 = ∑ i = 1 n b i b i ˉ = ∑ i = 1 n ∣ b i ∣ 2 ||v||^2=\sum_{\\i=1}^n b_i\bar{b_i}=\sum_{i=1}^n|b_i|^2 ∣∣v∣∣2=∑i=1nbibiˉ=∑i=1n∣bi∣2。
-
正交投影向量定义
如果 S S S是内积空间 V V V的子空间,令 b ∈ V b\in V b∈V,如果存在向量 p ∈ S , q p\in S,q p∈S,q,使得 q ⊥ S , b = p + q q\perp S,b=p+q q⊥S,b=p+q,则称 p p p是 b b b在子空间 S S S上的正交投影向量。
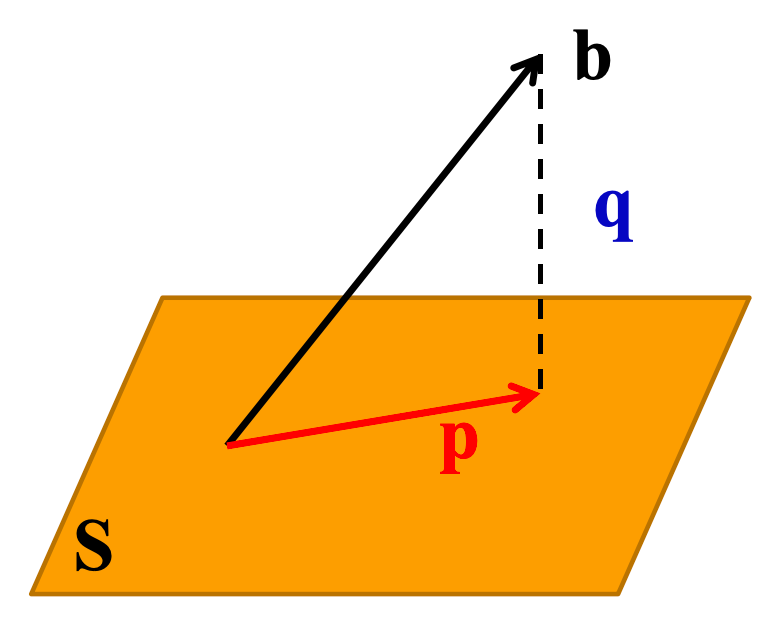
设 u 1 , ⋯ , u n u_1,\cdots ,u_n u1,⋯,un为 S S S的标准正交基,如果 p = ∑ i = 1 n ( b , u i ) u i p=\sum_{\\i=1}^n(b,u_i)u_i p=∑i=1n(b,ui)ui,则
-
b − p b-p b−p与 s s s的任意一个向量正交
-
p p p是 S S S中唯一一个最接近 b b b的向量。也就是说 ∀ y ∈ S , y ≠ p \forall y\in S,y \neq p ∀y∈S,y=p,有 ∣ ∣ y − b ∣ ∣ > ∣ ∣ p − b ∣ ∣ ||y-b||>||p-b|| ∣∣y−b∣∣>∣∣p−b∣∣。向量 p p p是 b b b在子空间 S S S上的正交投影向量。
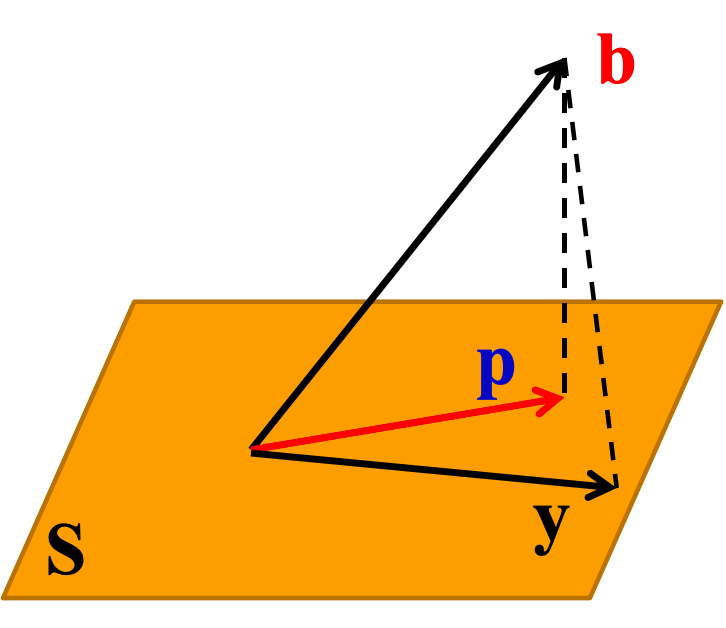
-
-
投影矩阵
设 S S S是内积空间 F n F^n Fn的非零子空间, b ∈ F n b\in F^n b∈Fn, u 1 , ⋯ , u n u_1,\cdots,u_n u1,⋯,un为 S S S的标准正交基, U = { u 1 , ⋯ , u n } U=\{u_1,\cdots,u_n\} U={u1,⋯,un},则 b b b在子空间 S S S的正交投影 p = U U H b p=UU^Hb p=UUHb,其中 U U U则是投影矩阵。
3 Gram-Schmidt正交化方法
设 α 1 , ⋯ , α n \alpha_1,\cdots,\alpha_n α1,⋯,αn是向量空间 V V V的线性无关向量组。我们按照以下步骤标准正交化得到标准正交向量组 β 1 , ⋯ , β n \beta_1,\cdots,\beta_n β1,⋯,βn
- 单位化向量 α 1 \alpha_1 α1,得到 β 1 = α 1 ∣ ∣ α 1 ∣ ∣ \beta_1=\frac{\alpha_1}{||\alpha_1||} β1=∣∣α1∣∣α1。易知 s p a n ( α 1 ) = s p a n ( β 1 ) span(\alpha_1)=span(\beta_1) span(α1)=span(β1)。
- 找到 α 2 \alpha_2 α2在 s p a n ( β 1 ) span(\beta_1) span(β1)上的向量投影 p 1 = ( α 2 , β 1 ) β 1 p_1=(\alpha_2,\beta_1)\beta_1 p1=(α2,β1)β1,根据推导可知 α 2 − p 1 \alpha_2-p_1 α2−p1和 s p a n ( β 1 ) span(\beta_1) span(β1)正交。我们对其单位化得到 β 2 = α 2 − p 1 ∣ ∣ α 2 − p 1 ∣ ∣ \beta_2=\frac{\alpha_2-p_1}{||\alpha_2-p_1||} β2=∣∣α2−p1∣∣α2−p1。易得 s p a n ( α 1 , α 2 ) = s p a n ( β 1 , β 2 ) span(\alpha_1,\alpha_2)=span(\beta_1,\beta_2) span(α1,α2)=span(β1,β2)。
- 找到 α 3 \alpha_3 α3在 s p a n ( β 1 , β 2 ) span(\beta_1,\beta_2) span(β1,β2)上的向量投影 p 2 = ( α 3 , β 1 ) β 1 + ( α 3 , β 2 ) β 2 p_2=(\alpha_3,\beta_1)\beta_1+(\alpha_3,\beta_2)\beta_2 p2=(α3,β1)β1+(α3,β2)β2,根据推导可知 α 3 − p 2 \alpha_3-p_2 α3−p2和 s p a n ( β 1 , β 2 ) span(\beta_1,\beta_2) span(β1,β2)正交。我们对其单位化得到 β 3 = α 3 − p 2 ∣ ∣ α 3 − p 2 ∣ ∣ \beta_3=\frac{\alpha_3-p_2}{||\alpha_3-p_2||} β3=∣∣α3−p2∣∣α3−p2。易得 s p a n ( α 1 , α 2 , α 3 ) = s p a n ( β 1 , β 2 , β 3 ) span(\alpha_1,\alpha_2,\alpha_3)=span(\beta_1,\beta_2,\beta_3) span(α1,α2,α3)=span(β1,β2,β3)。
- 如上进行操作, α i \alpha_i αi在 S i − 1 = s p a n ( α 1 , ⋯ , α i ) = s p a n ( β 1 , ⋯ , β i ) S_{i-1}=span(\alpha_1,\cdots,\alpha_i)=span(\beta_1,\cdots,\beta_i) Si−1=span(α1,⋯,αi)=span(β1,⋯,βi)的向量投影 p i − 1 = ( α i , β 1 ) β 1 + ⋯ + ( α i , β i − 1 ) β i − 1 p_{i-1}=(\alpha_i,\beta_1)\beta_1+\cdots+(\alpha_i,\beta_{i-1})\beta_{i-1} pi−1=(αi,β1)β1+⋯+(αi,βi−1)βi−1,则 α i − p i − 1 \alpha_i-p_{i-1} αi−pi−1和 S i − 1 S_{i-1} Si−1正交。所以对其单位化得到 β i = α i − p i − 1 ∣ ∣ α i − p i − 1 ∣ ∣ \beta_i=\frac{\alpha_i-p_{i-1}}{||\alpha_i-p_{i-1}||} βi=∣∣αi−pi−1∣∣αi−pi−1。易得 s p a n ( α 1 , ⋯ , α i ) = s p a n ( β 1 , ⋯ , β i ) span(\alpha_1,\cdots,\alpha_{i})=span(\beta_1,\cdots,\beta_{i}) span(α1,⋯,αi)=span(β1,⋯,βi)。
- 直到求得 β n \beta_n βn,得到标准正交向量组 β 1 , ⋯ , β n \beta_1,\cdots,\beta_n β1,⋯,βn
4 正交子空间
-
正交子空间定义
X , Y X,Y X,Y是内积空间 V V V的子空间,如果 ∀ x ∈ X , y ∈ Y \forall x\in X,y\in Y ∀x∈X,y∈Y, ( x , y ) = 0 (x,y)=0 (x,y)=0,则 X X X和 Y Y Y正交,我们记作 X ⊥ Y X\perp Y X⊥Y。
-
正交补定义
设 Y Y Y是内积空间 V V V的子空间,则 V V V中与 Y Y Y的每个向量正交的所有向量称为 Y ⊥ Y^{\perp} Y⊥, Y ⊥ = { x ∈ V ∣ ∀ y ∈ Y , ( x , y ) = 0 } Y^\perp =\{x\in V|\forall y\in Y,(x,y)=0 \} Y⊥={x∈V∣∀y∈Y,(x,y)=0}。
-
正交子空间定理
如果 V 1 V_1 V1和 V 2 V_2 V2正交,则 V 1 + V 2 V_1+V_2 V1+V2的和为直和。
-
正交补性质
设 S S S为有限维内积空间 V V V的子空间,则:
- V = S ⊕ S ⊥ V=S\oplus S^\perp V=S⊕S⊥。并且如果 V = S ⊕ W , W ⊥ S V=S\oplus W,W\perp S V=S⊕W,W⊥S,则 W = S ⊥ W=S^\perp W=S⊥。
- ( S ⊥ ) ⊥ = S (S^{\perp})^{\perp}=S (S⊥)⊥=S
-
向量到子空间的最小距离
设 S S S为有限维内积空间 V V V的子空间, ∀ b ∈ V \forall b\in V ∀b∈V,则 S S S 中的给定向量 p p p 与给定向量 b b b 最接近,当且仅当 b − p ⊥ S ⊥ b-p\perp S^{\perp} b−p⊥S⊥。即 p p p是 b b b在 S S S上的向量投影。
-
矩阵的基本子空间
设 A A A为 m × n m\times n m×n矩阵,则
N ( A ) = { x ∈ F n ∣ A x = 0 } N(A)=\{x\in F^n|Ax=0\} N(A)={x∈Fn∣Ax=0}: A A A的零空间, F n F^n Fn的子空间。
R ( A ) = A x ∣ x ∈ F n R(A)={Ax|x\in F^n} R(A)=Ax∣x∈Fn: A A A的列空间, F m F^m Fm的子空间。
N ( A H ) N(A^H) N(AH): A H A^H AH的零空间, F m F^m Fm的子空间。
R ( A H ) R(A^H) R(AH): A H A^H AH的列空间, F n F^n Fn的子空间。
N ( A ) = R ( A H ) ⊥ , N ( A h ) = R ( A ) ⊥ N(A)=R(A^H)^\perp,N(A^h)=R(A)^\perp N(A)=R(AH)⊥,N(Ah)=R(A)⊥
F n = N ( A ) ⊕ N ( A ) ⊥ = N ( A ) ⊕ R ( A H ) F^n=N(A)\oplus N(A)^\perp=N(A)\oplus R(A^H) Fn=N(A)⊕N(A)⊥=N(A)⊕R(AH)
dim ( F n ) = dim ( N ( A ) ) + dim ( R ( A H ) ) \dim(F^n)=\dim(N(A))+\dim(R(A^H)) dim(Fn)=dim(N(A))+dim(R(AH))
5 最小二乘问题
-
问题定义
设线性系统 A x = b Ax=b Ax=b,其中 A ∈ F m × n A\in F^{m\times n} A∈Fm×n,可能不相容(无解)。我们能否找到一个最佳解,即向量 x ^ \hat{x} x^使得 A x ^ − b = min x ∈ F n ∣ ∣ A x − b ∣ ∣ A\hat{x}-b=\min_{\\x\in F^n}||Ax-b|| Ax^−b=minx∈Fn∣∣Ax−b∣∣
-
问题核心
找到向量 x ^ \hat{x} x^即是使得 A x ^ A\hat{x} Ax^等于 b b b在 R ( A ) R(A) R(A)上的向量投影。
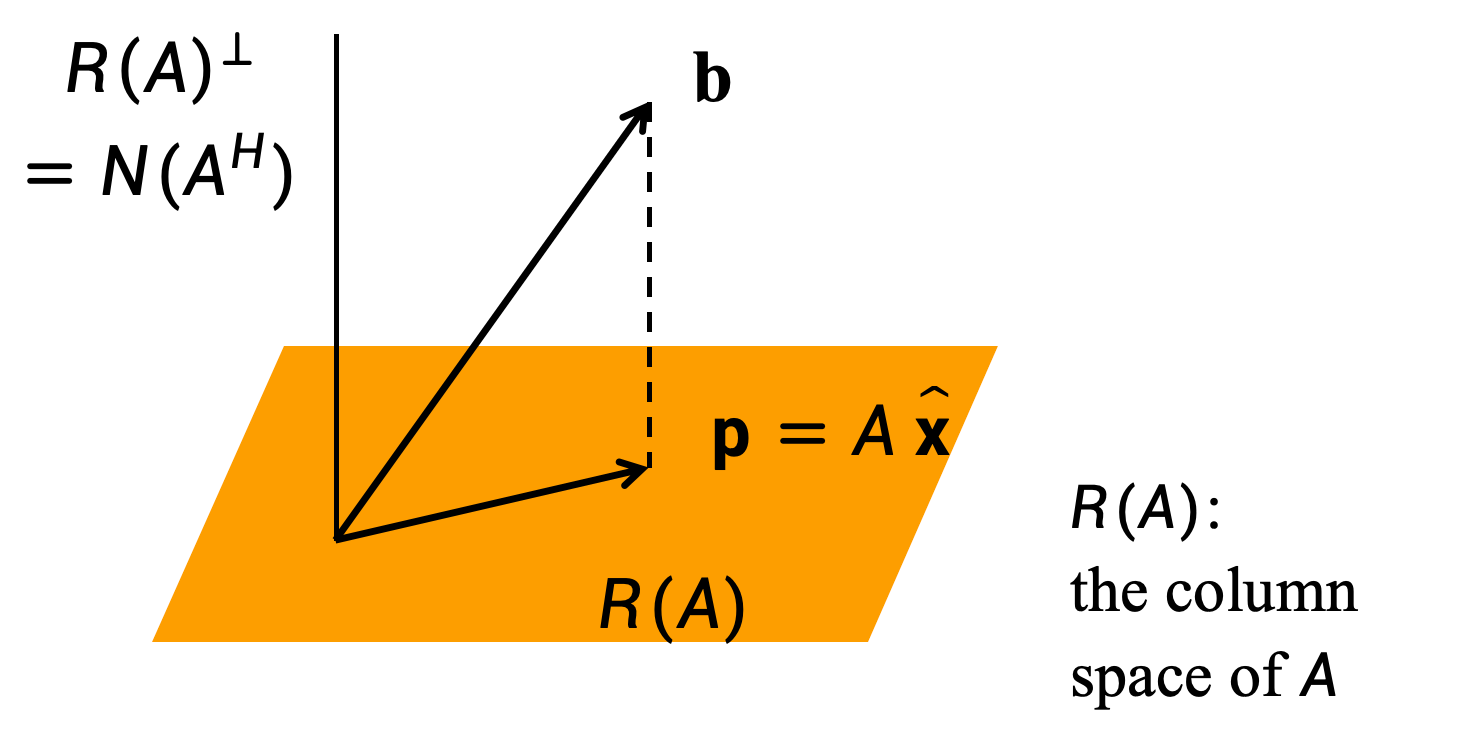
-
最小二乘解等价条件
- x ^ \hat{x} x^是 A x = b Ax=b Ax=b的最小二乘解
- A x ^ − b = min x ∈ F n ∣ ∣ A x − b ∣ ∣ A\hat{x}-b=\min_{\\x\in F^n}||Ax-b|| Ax^−b=minx∈Fn∣∣Ax−b∣∣
- A x ^ A\hat{x} Ax^等于 b b b在 R ( A ) R(A) R(A)上的正交向量投影
- A x ^ − b ∈ R ( A ) ⊥ = N ( A H ) A\hat{x}-b\in R(A)^\perp =N(A^H) Ax^−b∈R(A)⊥=N(AH)
- A H ( A x ^ − b ) = 0 A^H(A\hat{x}-b)=0 AH(Ax^−b)=0
- A H A x ^ = A H b A^HA\hat{x}=A^Hb AHAx^=AHb(正规方程)
-
正规方程的相容性
设 A ∈ F m × n A\in F^{m\times n} A∈Fm×n,则正规方程 A H A x = A H b A^HAx=A^Hb AHAx=AHb有解,其为 A x = b Ax=b Ax=b的最小二乘解。
最小二乘解不唯一,但是对于任意解 x , y x,y x,y, A x = A y Ax=Ay Ax=Ay,且 A x Ax Ax和 A y Ay Ay都是 b b b在 R ( A ) R(A) R(A)上的向量投影。
-
最小二乘解唯一解
设 A ∈ F m × n A\in F^{m\times n} A∈Fm×n,且 r a n k ( A ) = n rank(A)=n rank(A)=n(列满秩), b ∈ F n b\in F^n b∈Fn,则正规方程 A H A x = A H b A^HAx=A^Hb AHAx=AHb有唯一解 x ^ = ( A H A ) − 1 A H b \hat{x}=(A^HA)^{-1}A^Hb x^=(AHA)−1AHb。 x ^ \hat{x} x^为 A x − b Ax-b Ax−b的唯一最小二乘解。
6 正交矩阵和酉矩阵
-
正交矩阵定义
设 A ∈ R n × n A\in R^{n\times n} A∈Rn×n, A A A的所有列向量构成 R n R^n Rn的标准正交集,具有 R n R^n Rn上的标准内积。
-
酉矩阵定义
设 A ∈ C n × n A\in C^{n\times n} A∈Cn×n, A A A的所有列向量构成 C n C^n Cn的标准正交集,具有 C n C^n Cn上的标准内积。
易知,正交矩阵也是酉矩阵。
-
正交矩阵和酉矩阵的充要条件
A A A是正交矩阵当且仅当 A T A = I A^TA=I ATA=I
A A A是酉矩阵当且仅当 A H A = I A^HA=I AHA=I
-
若 A ∈ C n × n A\in C^{n\times n} A∈Cn×n,则以下条件等价
- A A A是酉矩阵
- A A A的列向量构成 C n C^n Cn的标准正交集
- A H A = I A^HA=I AHA=I
- A − 1 = A H A^{-1}=A^H A−1=AH
- ∀ x , y ∈ C n , ( A x , A y ) = ( x , y ) \forall x,y \in C^n,(Ax,Ay)=(x,y) ∀x,y∈Cn,(Ax,Ay)=(x,y)
- ∀ x ∈ C n , ( A x , A x ) = ( x , x ) \forall x\in C^n,(Ax,Ax)=(x,x) ∀x∈Cn,(Ax,Ax)=(x,x)