U-GAT-IT 使用指南
- 网络结构
- 优化目标
论文地址:https://arxiv.org/pdf/1907.10830.pdf
项目代码:https://github.com/taki0112/UGATIT
U-GAT-IT 和 Pix2Pix 的区别:
-
U-GAT-IT:主要应用于图像风格转换、图像翻译和图像增强等任务,适用于将图像从一个领域转换到另一个领域的应用。
-
PIX2PIX:主要应用于图像转换任务,例如将线稿转换为彩色图像、将语义标签转换为真实图像等,适用于输入和输出之间存在明确映射关系的应用。
网络结构
生成器:

注意力机制 CAM:全局池化和平均池化的类激活图。
-
假设我们要对一张狗的图片进行分类,判断它是不是一只狗。我们使用了一个卷积神经网络(CNN)进行分类,并得到了一个类激活图(CAM)。
-
在这张狗的图片中,CAM显示了狗的脸部区域比较亮,其他区域较暗。这意味着网络在分类时主要关注狗的脸部来判断它是否是一只狗。

实现方式是,通过权重(生成器图的 w 1 、 w 2 、 w 3 w_{1}、w_{2}、w_{3} w1、w2、w3):
- 特征图编码:输入图片经过下采样、残差模块,卷积提取特征,得到特征图
- 通道注意力:每个特征图对应一个权重 w,N 个特征图对应 N 个权重。权重就是通道注意力机制,每个通道对应不同特征(眼睛、鼻子、毛发、耳朵)
- 新特征图分类:新特征图的重要性,通过全连接层分类器学习,ta就知道了分类的核心特征是猫脸
判别器:
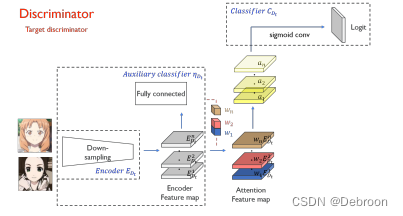
基本相同,也是通道注意力机制。
AdaLIN 结合了 Layer Normalization(LN)和 Instance Normalization(IN)各自的优点,实现归一化。
- LN:多个通道进行归一化,获取全局特征
- IN:各个图像特征图单独归一化,保留内容结构
把两者结合起来,互相抵消他们之间的不足,同时又结合了两者的优点。
最朴素的思想是寻找一个比率,来权衡某一层中 IN 与 LN 的关系:
- ρ ⋅ I N + ( 1 − ρ ) ⋅ L N \rho\cdot IN+(1-\rho)\cdot LN ρ⋅IN+(1−ρ)⋅LN
完整是这样:
- A d a L I N ( a , γ , β ) = γ ⋅ ( ρ ⋅ a ^ I + ( 1 − ρ ) ⋅ a L ^ ) + β a I ^ = a − μ I σ I 2 + ϵ , a L ^ = a − μ L σ L 2 + ϵ , ρ ← c l i p [ 0 , 1 ] ( ρ − τ Δ ρ ) \begin{aligned} AdaLIN& (a,\gamma,\beta)=\gamma\cdot(\rho\cdot\hat{a}_{I}+(1-\rho)\cdot\hat{a_{L}})+\beta \\ &\hat{a_{I}}=\frac{a-\mu_{I}}{\sqrt{\sigma_{I}^{2}+\epsilon}},\hat{a_{L}}=\frac{a-\mu_{L}}{\sqrt{\sigma_{L}^{2}+\epsilon}}, \\ &\rho\leftarrow clip_{[0,1]}(\rho-\tau\Delta\rho) \end{aligned} AdaLIN(a,γ,β)=γ⋅(ρ⋅a^I+(1−ρ)⋅aL^)+βaI^=σI2+ϵa−μI,aL^=σL2+ϵa−μL,ρ←clip[0,1](ρ−τΔρ)
这个公式是AdaLIN的具体计算公式,其中:
- a a a是输入特征图
- γ \gamma γ和 β \beta β是可学习的参数,分别用于缩放和偏移
- ρ \rho ρ是用于调整Layer Normalization和Instance Normalization的权重的参数
- a I ^ \hat{a_{I}} aI^和 a L ^ \hat{a_{L}} aL^是通过Instance Normalization和Layer Normalization对输入特征图进行归一化得到的结果
- μ I \mu_{I} μI和 σ I \sigma_{I} σI是Instance Normalization中计算的均值和标准差
- μ L \mu_{L} μL和 σ L \sigma_{L} σL是Layer Normalization中计算的均值和标准差
- ϵ \epsilon ϵ是一个小的常数,用于避免分母为0的情况
- c l i p [ 0 , 1 ] clip_{[0,1]} clip[0,1]表示将 ρ \rho ρ限制在0和1之间
- Δ ρ \Delta\rho Δρ是一个可学习的参数,用于更新 ρ \rho ρ
- τ \tau τ是一个调整步长的超参数
当 IN 更有用时, ρ \rho ρ 趋向于 1.
当 LN 更有用时, ρ \rho ρ 趋向于 0.
优化目标
对抗损失: L g a n s → t = E x ∼ X t ⌊ ( D t ( x ) ) 2 ⌋ + E x ∼ X s ⌊ ( 1 − D t ( G s → t ( x ) ) ) 2 ⌋ L_{gan}^{s\to t}=\operatorname{E}_{x\sim X_t}\left\lfloor(D_t(x))^2\right\rfloor+\operatorname{E}_{x\sim X_s}\left\lfloor(1-D_t(G_{s\to t}(x)))^2\right\rfloor Lgans→t=Ex∼Xt⌊(Dt(x))2⌋+Ex∼Xs⌊(1−Dt(Gs→t(x)))2⌋
- 判别是真实图像,还是生成图像
- s − > t s->t s−>t:S是真实图像(源域),T是生成图像(目标域)
- 源域和目标域:在图像翻译任务中,源域可以是一个领域(如马)的图像集合,而目标域可以是另一个领域(如斑马)的图像集合。我们的目标是将马的图像转换成斑马的图像。
- E x ∼ X t \operatorname{E}_{x\sim X_t} Ex∼Xt:图像来自真实目标域,即 x 从 X t X_t Xt 真实目标域取值
- 我们希望小猫咪能够像小狗狗一样学会叫声。我们让小猫咪通过观察小狗狗的叫声来学习。小猫咪会尝试发出自己的叫声,然后小狗狗会判断这个声音是不是来自于小狗狗。如果小狗狗认为声音是来自于小狗狗,那么我们会说小猫咪的叫声越接近真实的小狗狗叫声。
- D t ( x ) D_t(x) Dt(x) 表示小狗狗判别器对于真实目标域的小狗狗叫声 x x x的真实性判断。
- G s → t ( x ) G_{s\to t}(x) Gs→t(x) 是小猫咪通过模仿小狗狗学习到的叫声。
- D t ( G s → t ( x ) ) D_t(G_{s\to t}(x)) Dt(Gs→t(x)) 是小狗狗判断小猫咪模拟的叫声 G s → t ( x ) G_{s\to t}(x) Gs→t(x) 的真实性。
- 1 − D t ( G s → t ( x ) ) 1-D_t(G_{s\to t}(x)) 1−Dt(Gs→t(x)) 是小狗狗判断小猫咪模拟的叫声 G s → t ( x ) G_{s\to t}(x) Gs→t(x) 的不真实性(伪造概率)。
身份不变损失: L i d e n t i t y s → t = E x ∼ X t [ ∥ x − G s → t ( x ) ∥ 1 ] L_{identity}^{s\to t}=\operatorname{E}_{x\sim X_t}\left[\left\|x-G_{s\to t}(x)\right\|_1\right] Lidentitys→t=Ex∼Xt[∥x−Gs→t(x)∥1]
- 要把输入图片变成猫的图片,如果输入图片本身就是猫,那就不用变了。
循环一致性损失: L c y c l e s → t = E x ∼ X s [ ∣ x − G t → s ( G s → t ( x ) ) ∣ 1 ] L_{cycle}^{s\to t}=\operatorname{E}_{x\sim X_s}\left[\left|x-G_{t\to s}\left(G_{s\to t}(x)\right)\right|_1\right] Lcycles→t=Ex∼Xs[∣x−Gt→s(Gs→t(x))∣1]
- 正向变换过后,逆向还能变回来。
CAM 的生成器、判别器损失:
L
c
a
m
G
t
→
t
=
−
E
x
∼
X
s
[
log
(
η
s
(
x
)
)
]
+
E
x
∼
X
t
[
log
(
1
−
η
s
(
x
)
)
]
L
c
a
m
D
t
=
E
x
∼
X
t
[
(
η
D
t
(
x
)
)
2
]
+
E
x
∼
X
s
[
log
(
1
−
η
D
t
(
G
s
→
t
(
x
)
)
)
2
]
\begin{aligned}L_{cam}^{G_{t\to t}}&=-\mathrm{E}_{_{x\sim X_s}}\big[\log\big(\eta_s\big(x\big)\big)\big]+\mathrm{E}_{_{x\sim X_t}}\big[\log\big(1-\eta_s\big(x\big)\big)\big]\\\\L_{_{cam}}^{D_t}&=\mathrm{E}_{_{x\sim X_t}}\big[\big(\eta_{D_t}\big(x\big)\big)^2\big]+\mathrm{E}_{_{x\sim X_s}}\big[\log\big(1-\eta_{_{D_t}}\big(G_{_{s\to t}}\big(x\big)\big)\big)^2\big]\end{aligned}
LcamGt→tLcamDt=−Ex∼Xs[log(ηs(x))]+Ex∼Xt[log(1−ηs(x))]=Ex∼Xt[(ηDt(x))2]+Ex∼Xs[log(1−ηDt(Gs→t(x)))2]
优化目标: min G s → t , G t → s , η s , η t max D s , D t , η D s , η D t λ 1 L g a n + λ 2 L c y c l e + λ 3 L i d e n t i t y + λ 4 L c a m \min_{G_{s\to t},G_{t\to s},\eta_s,\eta_t}\max_{D_s,D_t,\eta_{D_s},\eta_{D_t}}\lambda_1L_{gan}+\lambda_2L_{cycle}+\lambda_3L_{identity}+\lambda_4L_{cam} minGs→t,Gt→s,ηs,ηtmaxDs,Dt,ηDs,ηDtλ1Lgan+λ2Lcycle+λ3Lidentity+λ4Lcam
- 权重: λ 1 = 1 , λ 2 = 10 , λ 3 = 10 , λ 4 = 1000. \begin{aligned}\lambda_1=1,\lambda_2=10,\lambda_3=10,\lambda_4=1000.\end{aligned} λ1=1,λ2=10,λ3=10,λ4=1000.
![用最少数量的箭引爆气球[中等]](https://img-blog.csdnimg.cn/direct/7b1313d956dc4aa1a66c61bb7585b4f0.png)