用最少数量的箭引爆气球[中等]

news2024/9/21 19:05:50

优质博文：IT-BLOG-CN

一、题目

有一些球形气球贴在一堵用XY平面表示的墙面上。墙面上的气球记录在整数数组points，其中points[i] = [xstart, xend]表示水平直径在xstart和xend之间的气球。你不知道气球的确切y坐标。一支弓箭可以沿着x轴从不同点完全垂直地射出。在坐标x处射出一支箭，若有一个气球的直径的开始和结束坐标为xstart，xend，且满足xstart ≤ x ≤ xend，则该气球会被引爆。可以射出的弓箭的数量没有限制。弓箭一旦被射出之后，可以无限地前进。

给你一个数组points，返回引爆所有气球所必须射出的最小弓箭数。

示例 1：
输入：points = [[10,16],[2,8],[1,6],[7,12]]
输出：2
解释：气球可以用2支箭来爆破:
-在x = 6处射出箭，击破气球[2,8]和[1,6]。
-在x = 11处发射箭，击破气球[10,16]和[7,12]。

示例 2：
输入：points = [[1,2],[3,4],[5,6],[7,8]]
输出：4
解释：每个气球需要射出一支箭，总共需要4支箭。

示例 3：
输入：points = [[1,2],[2,3],[3,4],[4,5]]
输出：2
解释：气球可以用2支箭来爆破:
-在x = 2处发射箭，击破气球[1,2]和[2,3]。
-在x = 4处射出箭，击破气球[3,4]和[4,5]。

1 <= points.length <= 105
points[i].length == 2
-231 <= xstart < xend <= 231 - 1

二、代码

排序 + 贪心： 我们首先随机地射出一支箭，再看一看是否能够调整这支箭地射出位置，使得我们可以引爆更多数目的气球。

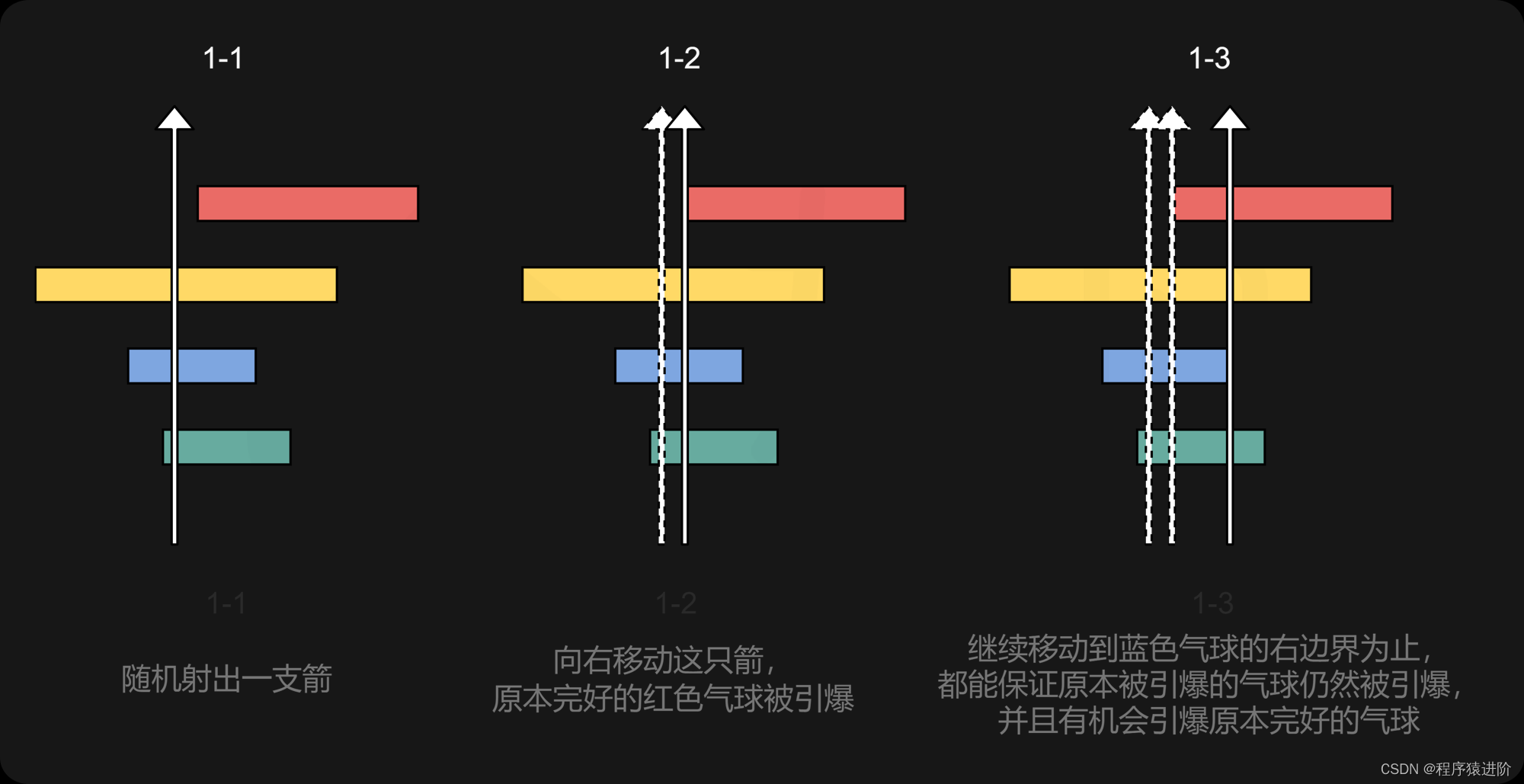
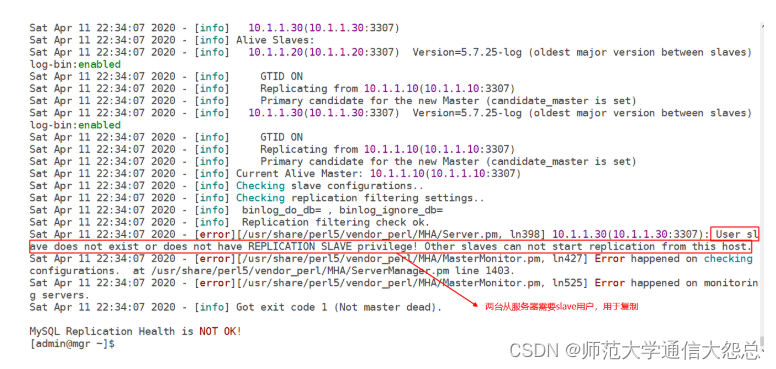
如图1-1所示，我们随机射出一支箭，引爆了除红色气球以外的所有气球。我们称所有引爆的气球为「原本引爆的气球」，其余的气球为「原本完好的气球」。可以发现，如果我们将这支箭的射出位置稍微往右移动一点，那么我们就有机会引爆红色气球，如图1-2所示。那么我们最远可以将这支箭往右移动多远呢？我们唯一的要求就是：原本引爆的气球只要仍然被引爆就行了。这样一来，我们找出原本引爆的气球中右边界位置最靠左的那一个，将这支箭的射出位置移动到这个右边界位置，这也是最远可以往右移动到的位置：如图1-3所示，只要我们再往右移动一点点，这个气球就无法被引爆了。

为什么「原本引爆的气球仍然被引爆」是唯一的要求？别急，往下看就能看到其精妙所在。

因此，我们可以断定：一定存在一种最优（射出的箭数最小）的方法，使得每一支箭的射出位置都恰好对应着某一个气球的右边界。

这是为什么？我们考虑任意一种最优的方法，对于其中的任意一支箭，我们都通过上面描述的方法，将这支箭的位置移动到它对应的「原本引爆的气球中最靠左的右边界位置」，那么这些原本引爆的气球仍然被引爆。这样一来，所有的气球仍然都会被引爆，并且每一支箭的射出位置都恰好位于某一个气球的右边界了。

有了这样一个有用的断定，我们就可以快速得到一种最优的方法了。考虑所有气球中右边界位置最靠左的那一个，那么一定有一支箭的射出位置就是它的右边界（否则就没有箭可以将其引爆了）。当我们确定了一支箭之后，我们就可以将这支箭引爆的所有气球移除，并从剩下未被引爆的气球中，再选择右边界位置最靠左的那一个，确定下一支箭，直到所有的气球都被引爆。

我们可以写出如下的伪代码：

let points := [[x(0), y(0)], [x(1), y(1)], ... [x(n-1), y(n-1)]]，表示 n 个气球
let burst := [false] * n，表示每个气球是否被引爆
let ans := 1，表示射出的箭数

将 points 按照 y 值（右边界）进行升序排序

while burst 中还有 false 值 do
    let i := 最小的满足 burst[i] = false 的索引 i
    for j := i to n-1 do
        if x(j) <= y(i) then
            burst[j] := true
        end if
    end for
end while

return ans

这样的做法在最坏情况下时间复杂度是O(n^2)，即这n个气球对应的区间互不重叠，while循环需要执行n次。那么我们如何继续进行优化呢？

事实上，在内层的j循环中，当我们遇到第一个不满足x(j)≤y(i)的j值，就可以直接跳出循环，并且这个y(j)就是下一支箭的射出位置。为什么这样做是对的呢？我们考虑某一支箭的索引it以及它的下一支箭的索引jt，对于索引在jt之后的任意一个可以被it引爆的气球，记索引为j0，有：x(j0)≤y(it)由于y(it)≤y(jt)显然成立，那么x(j0)≤y(jt)也成立，也就是说：当前这支箭在索引jt（第一个无法引爆的气球）之后所有可以引爆的气球，下一支箭也都可以引爆。因此我们就证明了其正确性，也就可以写出如下的伪代码：

let points := [[x(0), y(0)], [x(1), y(1)], ... [x(n-1), y(n-1)]]，表示 n 个气球
let pos := y(0)，表示当前箭的射出位置
let ans := 1，表示射出的箭数

将 points 按照 y 值（右边界）进行升序排序

for i := 1 to n-1 do
    if x(i) > pos then
        ans := ans + 1
        pos := y(i)
    end if
end for

return ans

这样就可以将计算答案的时间从O(n^2)降低至O(n)。

class Solution {
    public int findMinArrowShots(int[][] points) {
        if (points.length == 0) {
            return 0;
        }
        Arrays.sort(points, new Comparator<int[]>() {
            public int compare(int[] point1, int[] point2) {
                if (point1[1] > point2[1]) {
                    return 1;
                } else if (point1[1] < point2[1]) {
                    return -1;
                } else {
                    return 0;
                }
            }
        });
        int pos = points[0][1];
        int ans = 1;
        for (int[] balloon: points) {
            if (balloon[0] > pos) {
                pos = balloon[1];
                ++ans;
            }
        }
        return ans;
    }
}