目录
- 四个子空间 Four subspaces
- 基和维数 Basis& Dimension
- 新向量空间 New vector space
本讲讨论矩阵的四个基本子空间以及他们之间的关系。
四个子空间 Four subspaces
任意的 m x n 矩阵 A 都定义了四个子空间。
- 列空间 Column space C(A)
矩阵 A 的列空间是 A 的列向量的线性组合在 R m R^m Rm空间中构成的子空间。 - 零空间 Nullspace N(A)
矩阵 A 的零空间是 Ax=0 的所有解 x 在 R n R^n Rn空间中构成的子空间。 - 行空间 Row space C(
A
T
A^T
AT)
矩阵 A 的行空间是 A 的行向量的线性组合在 R n R^n Rn空间中构成的子空间,也就是矩阵 AT的列空间。 - 左零空间 Left nullspace N(
A
T
A^T
AT)
我们称矩阵 AT的零空间为矩阵 A 的左零空间,它是 R m R^m Rm空间中的子空间。
基和维数 Basis& Dimension
-
列空间
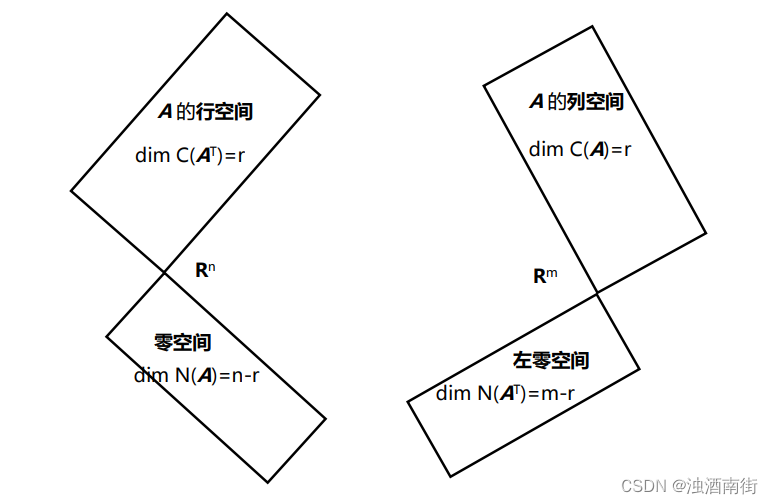
矩阵 A 的 r 个主元列构成了列空间 C(A)的一组基。dim C(A)=r -
零空间
Ax=0 的一组特解对应于矩阵 A 的 n-r 个自由列,并构成了零空间的一组基。dim N(A)=n-r -
行空间
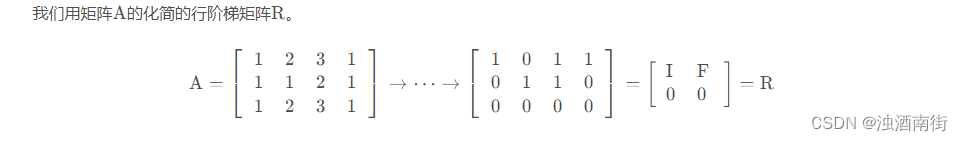
尽管矩阵 A 和矩阵 R 的列空间不同,但两者行空间相同。R 的行向量来自于 A的行向量的线性组合,因为消元操作是可逆的,所以 A 的向量也可以表示为 R 行向量的线性组合。 R 的前 r 行阶梯型“行向量”就是矩阵 A 行空间 C( A T A^T AT)的一组基。dim C( A T A^T AT)=r -
左零空间
矩阵 A T A^T AT有 m 列,而其秩为 r,因此其自由列数目为 m-r。所以 dim N( A T A^T AT)=m-r。 左零矩阵是满足 A T A^T ATy=0 的所有向量 y 的集合。称之为左零矩阵是因为该式可写作 y T y^T yTA=0,而 y 出现在矩阵 A 左侧。
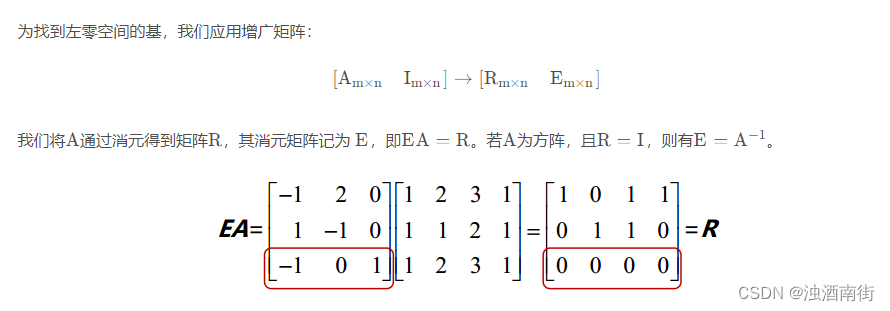
以“行操作”的观点来看矩阵 E 和 A 的乘法,则矩阵 E 最下面的 m-r 个行向量使得矩阵 A 的行向量线性组合成为 0,也就是矩阵 R 最下面的 m-r 个零向量。本例中,m-r=1。
矩阵 E 的这 m-r 个行向量满足 y T y^T yTA=0,它组成了矩阵 A 左零空间的一组基。
新向量空间 New vector space
所有 3X3 矩阵构成的集合是一个向量空间,符合对于线性运算封闭,称之为 M。
M 的子空间包括: 所有的上三角阵,所有的对称阵,所有的对角阵
对角阵是前两个子空间的交集,其维数为 3,具有以下一组基:
[
1
0
0
0
0
0
0
0
0
]
[
0
0
0
0
1
0
0
0
0
]
[
0
0
0
0
0
0
0
0
1
]
\begin{bmatrix} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix} \begin{bmatrix} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{bmatrix} \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix}
100000000
000010000
000000001