Decision tree
知识树
Knowledge tree

一个小故事
A story
挑苹果:
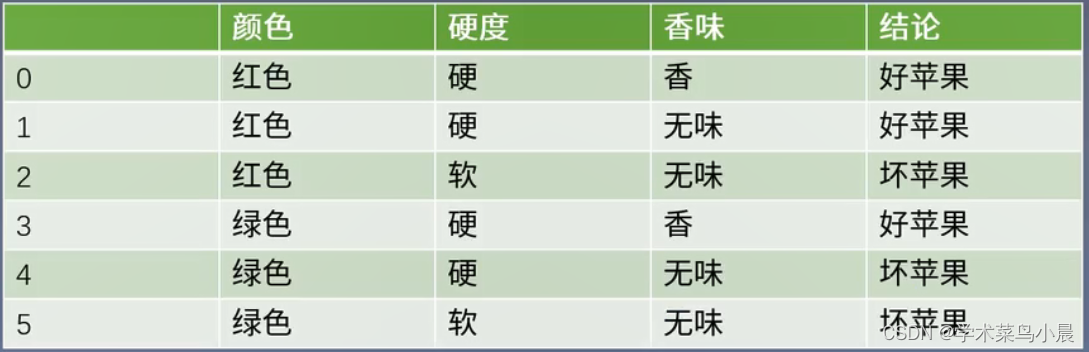
根据这些特征,如颜色是否是红色、硬度是否是硬、香味是否是香,如果全部满足绝对是好苹果,或者红色+硬但是无味也是好苹果,从上图可以看出来,只要做足够的循环判断即可得到结果。
如下图:

一步步走下来,就能挑到好苹果。这就是决策树
-
最顶端的叫根节点,所有样本的预测都是从根节点开始。
-
每一个圆形节点表示判断,每个节点只对样本的某个属性进行判断。
-
圆形节点是标记节点,走到圆形节点表示判断结束,将圆形节点中的标签作为对应的预测结果。
如何构建决策树:
-
构建的决策树按顺序对每个特征进行判断(低效)
-
每个判断节点都尽可能让一半进入A分支,另一半进入B分支(高效)
引入新的知识,信息熵
信息熵
Information entropy
-
每走一步,我们都在确定苹果的好坏。
-
在根节点时,我们对苹果的好坏一无所知。
-
经过对颜色的判断后,如果是红色,我们明白好坏的概率是1/2。虽然还包含了1/2的不确定性。
-
如果苹果红色的前提下又硬,我们100%确定它是好苹果。此时不确定性坍塌为0。
-
这是一个减少不确定性的过程。
从整体来讲,我们希望决策树每走一步,不确定性都下降的快一些,让我们的判断步数无限小。
什么是信息的不确定性?
就是信息熵
在信息论与概率统计中,熵(entropy)是表示随机变量不确定性的度量,设X是一个取有限个值的离散随机变量,其概率分布为

则随机变量X的熵定义为

面试可能会问到这个公式,还有交叉熵、相对熵
熵越大,则随机变量的不确定性越大。其中0 ≤ H(P) ≤ log n
举例计算
Example
假设投色子,6个的概率分别是1/6,计算如下:
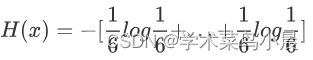
其中6个1/6(log左边的六分之一)加起来就是1

则最终=log6
这也解释了为什么上面H(P) ≤ log n
另外,均由分布的时候,熵最大,因为所有可能都是一样的,如上面的6个面都是1/6。
如果有1个坏苹果和9个好苹果时,我们可以认为大部分都是坏苹果。内部并不混乱,确定性很大,熵很小。
信息增益
Information gain
表示得知特征X的信息而使得类Y的信息的不确定性减少的程度。
特征A对训练集D的信息增益g(D,A),定义为集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差,即:g(D, A) = H(D) - H(D|A)
当前的信息熵等于划分完(如划分成两个)的信息熵之和。
信息增益算法
输入:训练数据集D和特征A
输出:特征A对训练数据集D的信息
-
计算数据集D的经验熵H(D)

-
计算特征A对数据集D的经验条件熵H(D|A)

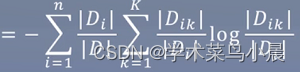
-
计算信息增益

举个例子
Example
是否信贷
| ID | 年龄 | 有工作 | 有自己房子 | 信贷情况 | 类别 |
|---|---|---|---|---|---|
| 1 | 青年 | 否 | 否 | 一般 | 否 |
| 2 | 青年 | 否 | 否 | 好 | 否 |
| 3 | 青年 | 是 | 否 | 好 | 是 |
| 4 | 青年 | 是 | 是 | 一般 | 是 |
| 5 | 青年 | 否 | 否 | 一般 | 否 |
| 6 | 中年 | 否 | 否 | 一般 | 否 |
| 7 | 中年 | 否 | 否 | 好 | 否 |
| 8 | 中年 | 是 | 是 | 好 | 是 |
| 9 | 中年 | 否 | 是 | 非常好 | 是 |
| 10 | 中年 | 否 | 是 | 非常好 | 是 |
| 11 | 老年 | 否 | 是 | 非常好 | 是 |
| 12 | 老年 | 否 | 是 | 好 | 是 |
| 13 | 老年 | 是 | 否 | 好 | 是 |
| 14 | 老年 | 是 | 否 | 非常好 | 是 |
| 15 | 老年 | 否 | 否 | 一般 | 否 |
对上表所给的训练数据集D,根据信息增益准则选择最优特征。首先计算经验熵H(D)

计算类别:一共15个类别,9个是,6个否
然后计算各特征对数据集D的信息增益,分别以A1,A2,A3,A4表示年龄、有工作、有自己房子和信贷情况4个特征,则
-
首先计算年龄

H(D)=0.971上面计算了,H(D1)青年,H(D2)中年,H(D3)老年
-
计算有工作

H(D)=0.971,H(D1)是有工作,H(D2)是无工作
-
计算有无房子
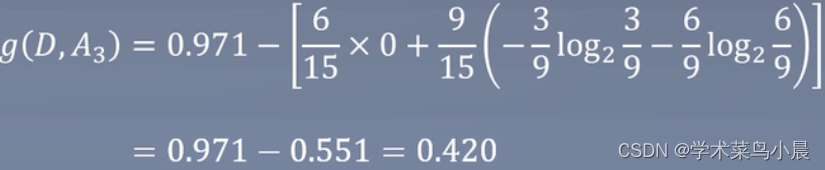
-
计算信贷情况

有无房子是作为信贷的第一个划分,下降的最快
信息增益比
Information gain ratio
信息增益比:
如果以信息增益为划分依据,存在偏向选择取值较多的特征,信息增益是对这一问题进行矫正。
举例:
如上面的例子,后面加入了身份证这个特征,身份证又是唯一的,算法对样本画了个15叉树,一层就搞定了全部的分类。
这样会造成一个问题,划分会倾向于特征取值数目较多的,即分的更快。
但在预测集上就出现很大的问题了,即预测集的身份证肯定也是唯一的。
定义:
特征A对训练数据集D的信息增益比

定义为其信息增益g(D,A)与训练数据集D关于特征A的经验熵H(D)之比:
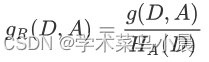
计算:
如上面的年龄,有3个类(青年、中年、老年),
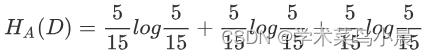
信息增益比和信息增益的区别就是除以

决策树的构建
Build the decision tree

C4.5算法,大体相同,只不过计算的是信息增益比,而不是信息增益。我们通常也是用C4.5作为决策树的算法,其区别也就在于多了个分母。
总结
Summarization
-
决策树的核心思想:以树结构为基础,每个节点对某特征进行判断,进入分支,直到到达叶节点。
-
决策树构造的核心思想:让信息熵快速下降,从而达到最少的判断次数获得标签。
-
判断信息熵下降速度的方法:信息增益。
-
构建决策树算法:ID3(使用信息增益)、C4.5(使用使用信息增益比)。
-
信息增益会导致节点偏向选取取值角度的特征的问题。
关于第5点的补充,统计学习和西瓜书都是给的这个解释,但还有另一种解释,就是信息增益导致大数问题——>概率是否准确的问题。