大家好，这里是大话硬件。
我们来回顾一下前面8讲的内容，主要对下面的知识点进行了分析：
系统框图

反馈环节传递函数

功率级传递函数

PWM级传递函数

传递函数计算

如果我们把开关电源看成是不同的电路模块拼接而成，现在已经知道了每个模块的传递函数，那么接下来的事情很简单，按照闭环控制系统求解传递函数的方法求解就行。

整个系统闭环起来就是下面这样:

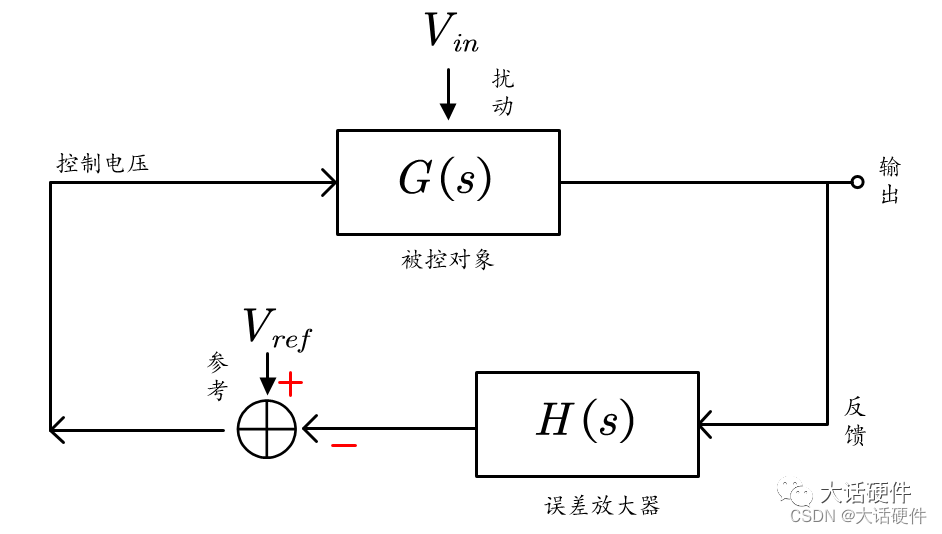
要求解上面系统的传递函数，就必须知道输入和输出。输出都知道是输出电压，但输入是什么呢？

从上面的框图可以看出 ，其实系统的输入有两个，一个是输入电压Vin，另外一个是参考电压Vref。

这么说可能不够形象，我们找个电源芯片的规格书看一下。

这个框图可以看出，电源内部会产生一个稳定的参考电压，将这个电压作为输入，输入到环路中。

假如我们将输入电压作为整个系统的输入，输出就是输出电压，那么传递函数就是输出/输入，其实这个在前面的文章中就已经求解出来了，也就是功率级的传递函数。

所以，如果输入电压是系统的输入，输入只经过了系统的一部分。

假设我们将参考电压作为整个系统的输入，输出还是输出电压，那么传递函数;

化简：

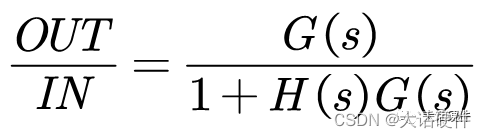
因此，如果参考电压是系统的输入，参考电压会经过环路。所以，整个系统的输入是参考电压，这里和我们常规的理解可能不一样，需要从传递函数的角度理解一下。

有了上面的结论，再把前面每个模块的传递函数级联起来，就可以得到开关电源系统的传递函数。当然，研究开关电源的传递函数不是目的，目的是判断电源系统是否稳定。

针对传递函数的分母

如果分母为0，那么传递函数的值就是无穷大，也就是说在输入信号为0的时候，输出也会存在，也就是我们常说的自激振荡。

要使系统不出现自激振荡，就需要满足一定的增益和相位条件，因此就引出了开关电源的稳定性判据。之前的文章分析过，这里不再赘述。

而分母出现零的条件是
幅值：

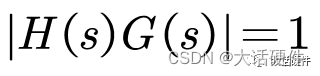
相位：

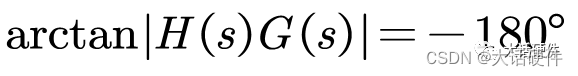
从增益和相位使分母为零的条件看稳定判据，其实稳定性判据就是要避免上述增益和相位的呈现！

分析到这里，我想很多人可能还是不太理解环路补偿到底是怎么一回事，下面我用比较好理解的方式概述一下。

第一步： 对于一个固定的电源系统，我们很容易求出控制到功率级的传递函数；

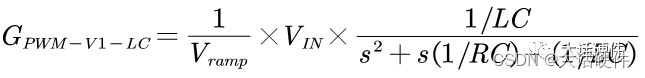
第二步： 我们把控制到输出传递函数的波特图画出来，此时有相位和增益；

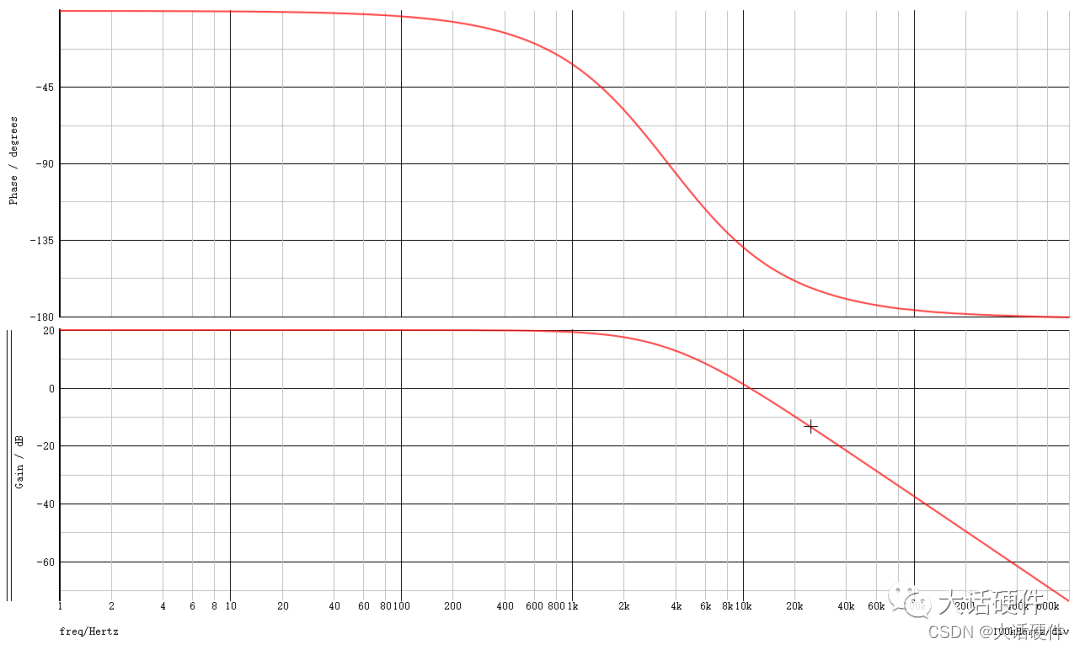
第三步： 我们已经掌握了一个电源要稳定需要什么样的稳定性条件；

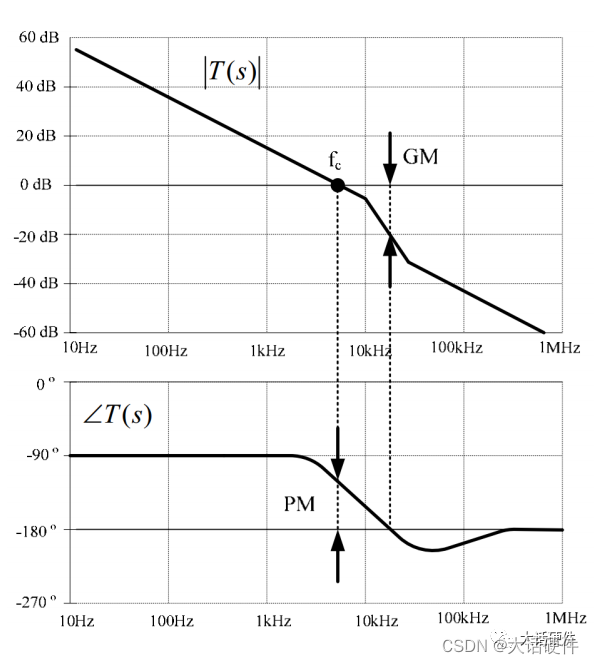
第四步： 观察第三步想要的增益和相位和实际第二步的增益和相位之间的差距，在什么频率需要增加增益，在什么位置需要提升相位，需要增加几个极点，几个零点，看图说话就能判断出来。

第五步：经过第四步的分析，基本知道了补偿系统需要提供哪些特性，因此利用放置零极点法，很容易将H（s）的特征表示出来；

第六步：结合我们之前分析的电压型和电流型分别有3种形态，通过放置合适的零极点来满足第5步的H（s）；

将符合要求的H（s）加入到反馈中，整个系统就会变得稳定，也就是实现了想要的增益和相位。

以上就是对开关电源环路补偿的理解。没有非常深的理论，也没有较多的公式，先帮大家建立起对环路补偿这件事到底是什么样的认知，有了这样的理解后，后面再针对一些细节进行分析会容易很多。