代数多重网格

你好！代数多重网格一个很有意思的话题。

问题定义

很多问题都可以抽象为求解下列优化的问题：

对于图像问题，一方面由于绝大多数模型都只会建立某个像素与它局部之间的关系，因此线性方程组的系数矩阵$A$通常满足某种特定的稀疏性；另一方面，由于图像分辨率较高，因此线性方程组维度实际上极大，导致快速计算难度较大。
因此，这个问题的****最终核心在于：如何快速求解一个稀疏大规模的对称正定的线性方程组。

迭代法的优畧

对于简单迭代法，如雅可比迭代，高斯-塞德尔迭代等，都存在高频快速收敛，低频难以收敛的问题。 简单来说，对于柏松问题：
在这里插入图片描述

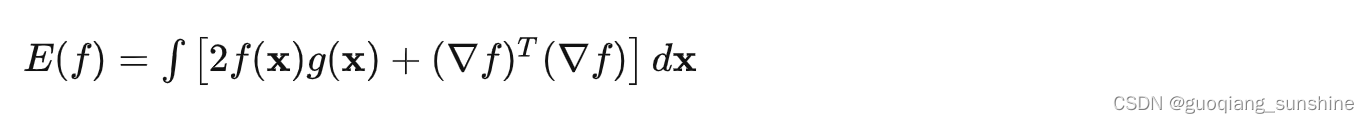
几何多重网格

为了解决低频收敛慢的问题，多重网格算法应运而生。 核心思想在于，在细网格上的低频可以变为粗网格上的高频。 注意到对于$ \lambda_{k}$ ，如果N变为N/2实际上可以认为频率变为了原来的两倍，那么收敛性自然会变好。 因此，我们可以先在细网格上迭代，消除了高频误差，然后放到粗网格迭代，消除细网格上的低频误差，然后再在粗网格上refine最终结果，大致流程如下图：

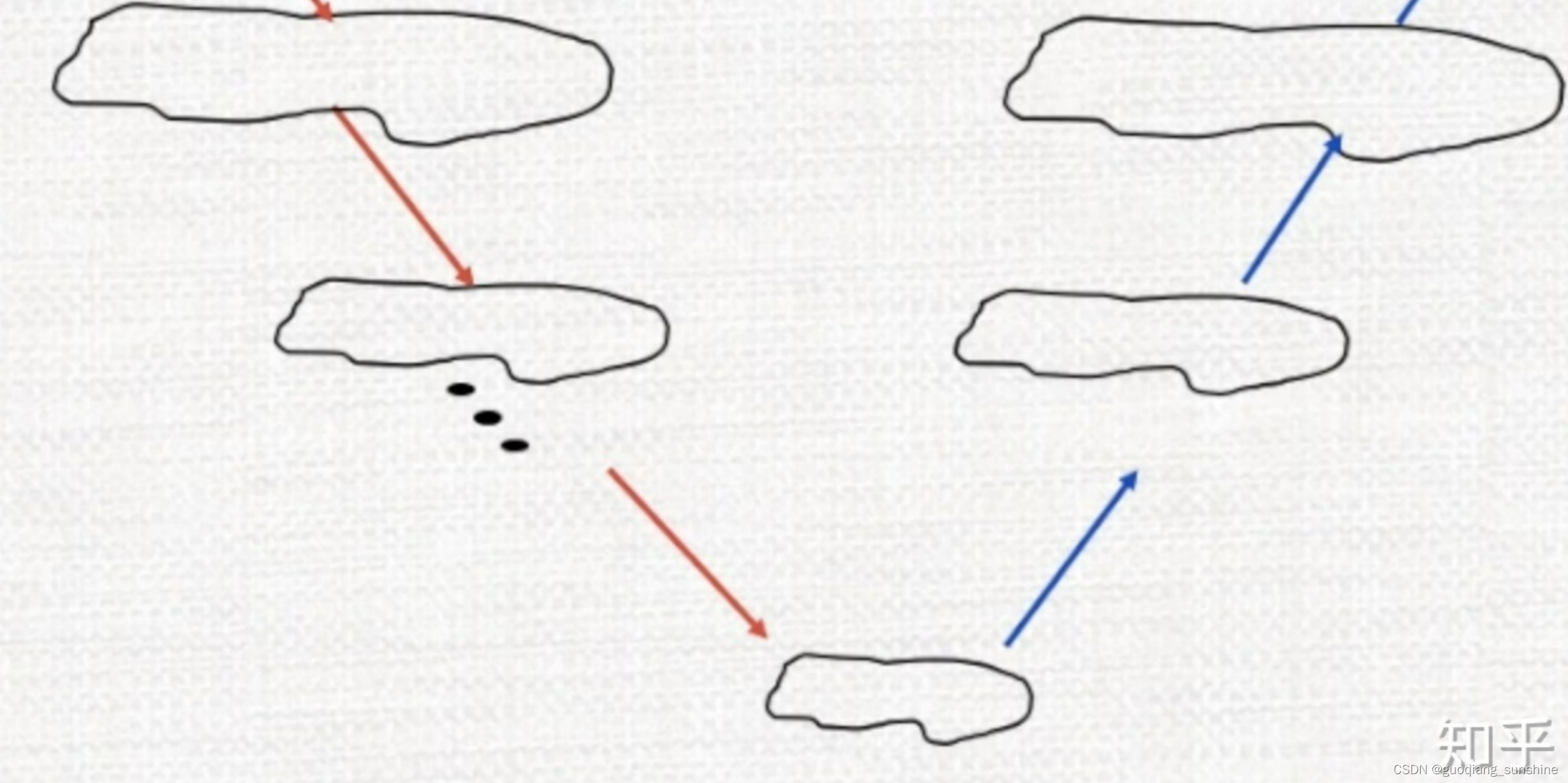
这个方法实际上是比较简单的，网格如下所示：

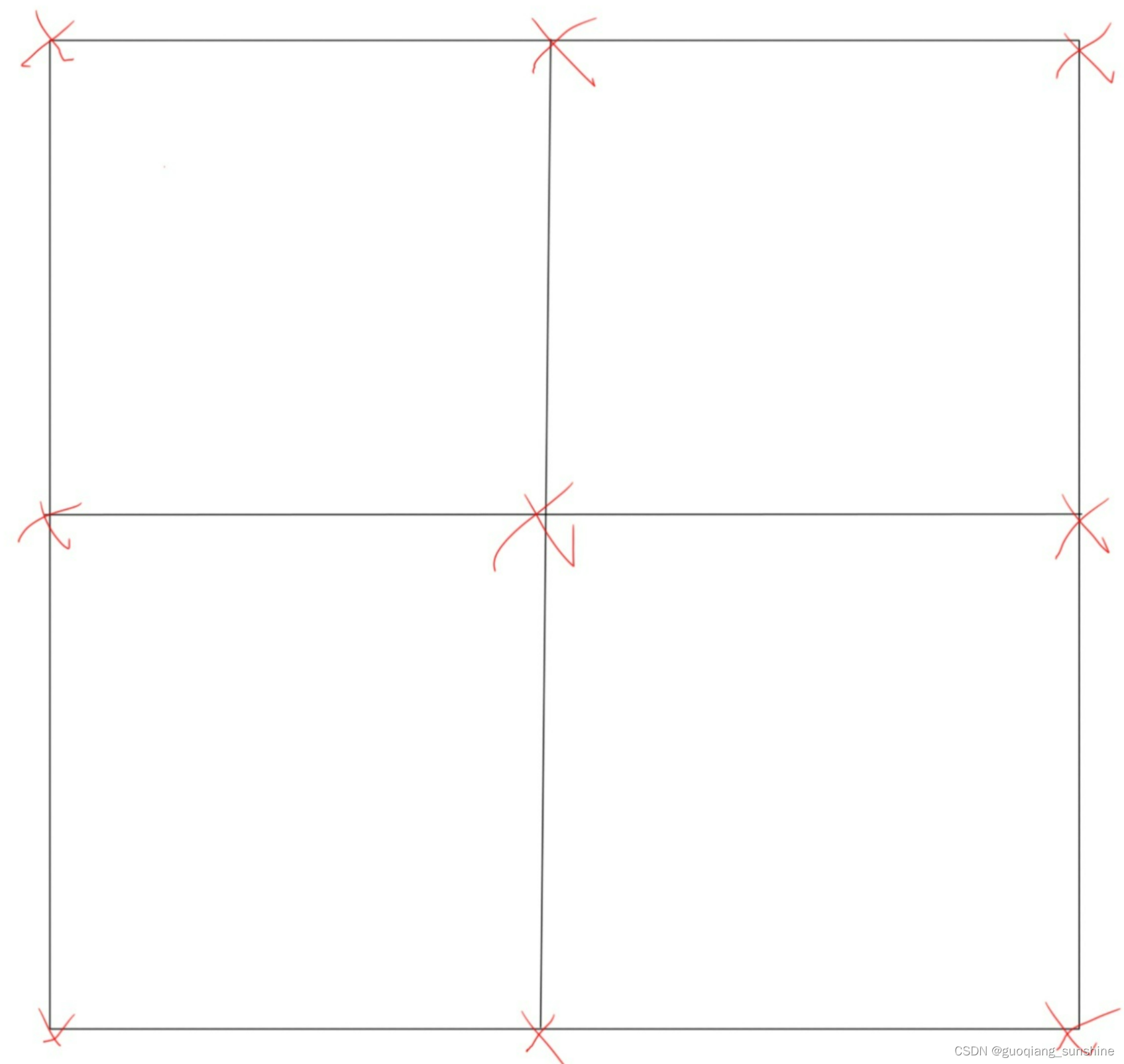
红色的点代表粗网格上的节点，如果我们将网格细化，那么，可以得到细网格的点：

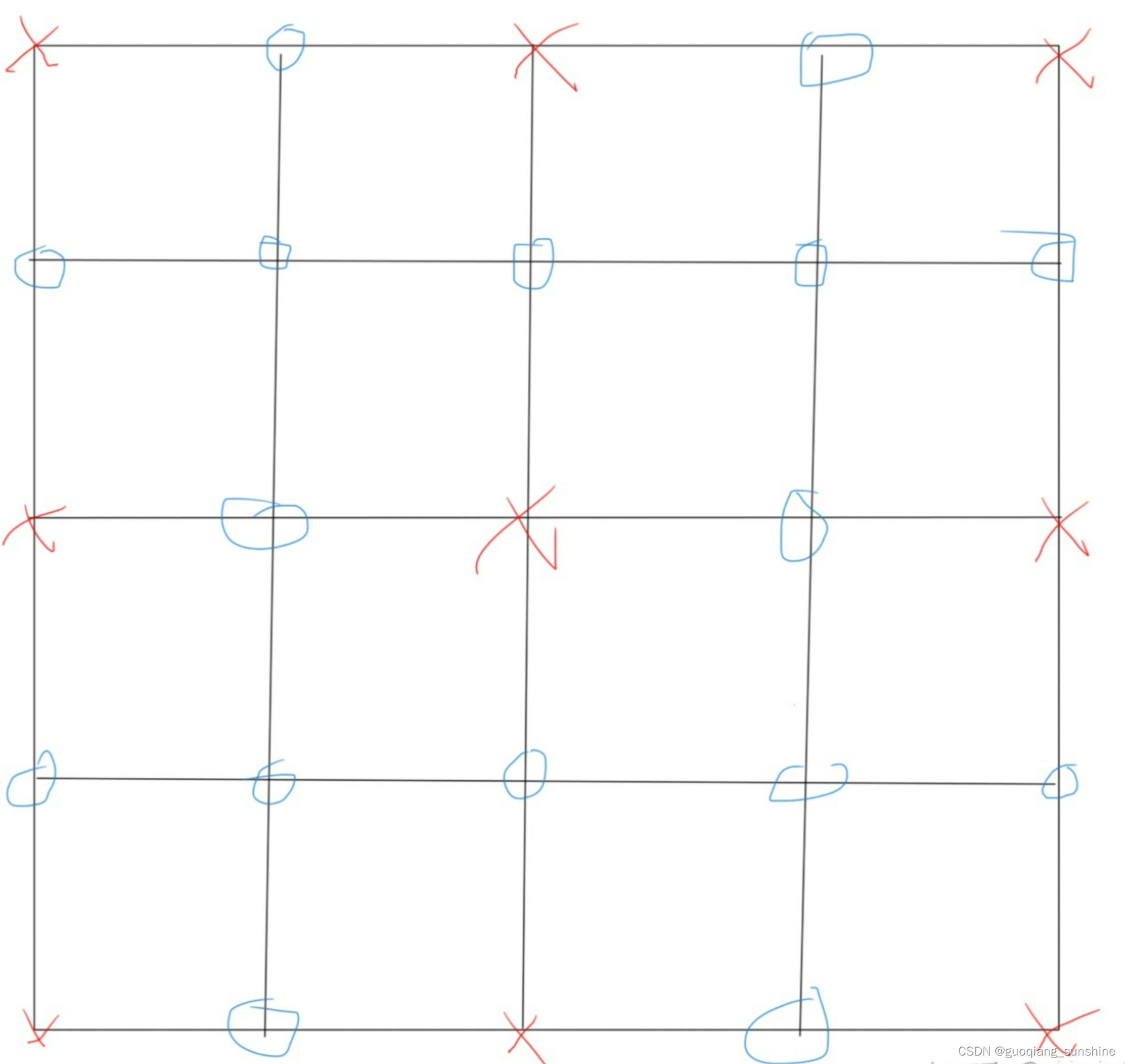
这些点的值通过粗网格插值而来，也就是说，几何多重网格实际上是依赖于实际的网格，人为设定了粗网格和细网格，从而设置的一种多重网格算法。

注意到这种方法细网格上的节点上一定有粗网格上的节点，因此原来如果粗细网格原来是同一个点，只需要将粗网格上的点赋值到细网格上，如果是新的点，那么需要对它进行插值，假设这个矩阵为$S,f_k$ 表示第k层网格上的节点，那么 $f_k=S\ast f_{k-1}$ ，因此我们只需要求解线性方程组：
$$A_{k-1}{f}_{k-1}=g_{k-1}$$
之后插值即可。

但实际上这样做是不对的。回到最初的问题，我们要消除的是低频误差，也就是“光滑”误差， 在粗网格上迭代后的结果实际上和光滑没有太多关系，我们迭代后的结果，实际上是消除了高频的误差，也就是将误差变得光滑了。 因此，我们将误差传到粗网格上实际上是更为合理的，因此我们最终的迭代思路实际上是不断修正误差，即：
$$f_k=f_0+\sum _{k=1}^M{e}_k$$
其中 $e_k$ 代表每层网格给出的插值后的补偿误差。
那么，如何建立误差方程呢？
定义残差:
$$E_k=A{f}_k-b$$
由此，我们有误差方程：$A{e}_k=E_k$
由于我们希望将低频误差放到粗网格上进行消除，因此我们实际上将$e_k$ “限制”到了粗网格上计算，然后再插值回粗网格上进行“误差补偿”。

最终，我们实际上计算了：
$$K_{k-1}{e}_{k-1}^{{}^{\prime }}=E_{k-1}$$
然后插值得到 $e_{k-1}=S\ast e_{k-1}^{{}^{\prime }}$
最后补偿到 f 上。

代数多重网格

是否有一种方法可以依赖于系数矩阵本身的特性，从而设计一种多重网格方法，与实际网格无关，从而得到更好的收敛性呢？实际上是有的，这个方法就是代数多重网格。 由于我们现在没有了实际网格，那么实际上为了使用多重网格技术，我们需要回答两个问题：

1. 要选择哪些节点为粗网格上的节点
2. 如何插值
   对于问题1，实际上我们是需要准从两个原则：得到的粗网格节点能够通过插值表示细网格节点，或者说粗网格节点一定原来有和细网格节点相连。另一方面，我们希望粗节点能够尽量少，从而求解线性方程组的规模可以更小。 对于这个问题有个经典方法: 即Ruge提出来的方法

对于问题2，回答了两个子问题：

1. 插值公式长什么样
   2)粗网格上的线性方程组长什么样

通常如果插值矩阵为$S_k$ ，那么粗网格上的线性方程组的系数矩阵构建为:KaTeX parse error: Expected group after '_' at position 2: S_̲^{T}_k A_kS_k

因此实际上核心还是在于如何插值。

假设 $a_{ij}$表示连接i和j节点的边的权重，同时我们认为残差几乎为0，由此可以得到:

$$r_i=a_{ii}{e}_i+\sum a_{ij}{e}_j\approx 0$$
由此:

$$a_{ii}{e}_i\approx -\sum a_{ij}{e}_j$$

由于这些边连接的节点可以分为3类：

细网格上的节点 $e_f$
粗网格上的节点 $e_c$
连接极弱的节点 $e_w$
若用C表示粗节点误差集合，F表示细节点误差集合，W表示弱连接集合，可以将求和部分分为三块：

$$a_{ii}{e}_i\approx -\sum _{j\in C}{a}_{ij}{e}_j-\sum _{j\in F}{a}_{ij}{e}_j$$
由于弱连接集合的连接已经足够弱，因此我们强制认为这部分的$e_j=e_i$ ,由此可以得到新的近似公式：

$$(a_{ii}+\sum _{j\in W}{a}_{ij})e_i\approx -\sum _{j\in C}{a}_{ij}{e}_j-\sum _{j\in F}{a}_{ij}{e}_j$$
对于粗网格上的$e_j$实际上在粗网格上已经算出，而细网格上的$e_j$ 实际上是没有的。 对于这部分有连接的细网格上的$e_j$ ，我们找到和它相连的所有粗网格的节点$e_{jc}$ ，通过公式：
$$e_j=\frac{\sum a_{j,jc}{e}_{jc}}{\sum a_{j,jc}}$$

对它进行近似计算。