题目

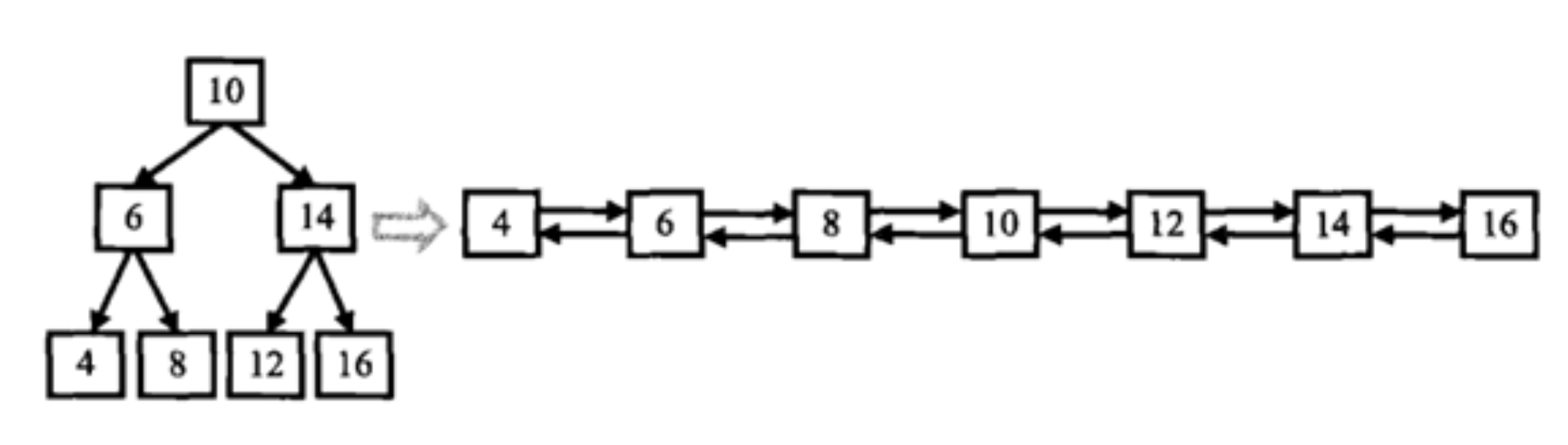
输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。如下图所示：

数据范围：输入二叉树的节点数0≤n≤1000，二叉树中每个节点的值0≤val≤1000.
要求：空间复杂度O(1)（即在原树上操作），时间复杂度 O(n)

注意:

1.要求不能创建任何新的结点，只能调整树中结点指针的指向。当转化完成以后，树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继。

2.返回链表中的第一个节点的指针。

3.函数返回的TreeNode，有左右指针，其实可以看成一个双向链表的数据结构。

4.你不用输出双向链表，程序会根据你的返回值自动打印输出。

输入描述：

二叉树的根节点

返回值描述：

双向链表的其中一个头节点。

示例1

输入：{10,6,14,4,8,12,16}

返回值：From left to right are:4,6,8,10,12,14,16;From right to left are:16,14,12,10,8,6,4;

说明：输入题面图中二叉树，输出的时候将双向链表的头节点返回即可。

示例2

输入：{5,4,#,3,#,2,#,1}

返回值：From left to right are:1,2,3,4,5;From right to left are:5,4,3,2,1;

说明：

                    5
                  /
                4
              /
            3
          /
        2
      /
    1

树的形状如上图。

---

思路

对于二分搜索树BST上的任意节点，左树中的所有节点值<根节点值<右树中的所有节点值，对其进行中序遍历，可得到升序集合。

递归将二叉树转为排序的双向链表：先转换左子树，并将转换后的左链表的尾节点与原树根节点相连；再转换右子树，并将原树根节点与转换后的右链表首节点相连。

---

代码

/**
public class TreeNode {
    int val = 0;
    TreeNode left = null;
    TreeNode right = null;

    public TreeNode(int val) {
        this.val = val;

    }
}
*/

public class Solution {
    //递归方法语义：传入一个BST的根节点，就可以将其转换为双向链表，且返回链表头
    public TreeNode Convert(TreeNode pRootOfTree) {
        //边界
        if(pRootOfTree == null || (pRootOfTree.left == null && pRootOfTree.right == null)) {
            return pRootOfTree;
        }

        //先转换左子树
        TreeNode left = Convert(pRootOfTree.left);
        //将转换后的左链表的尾节点与原树的根节点相连
        TreeNode leftTail = left;
        while(leftTail != null && leftTail.right != null) {
            leftTail = leftTail.right;
        }
        //此时leftTail指向左链表的尾节点，连接左链表尾节点和原树根节点
        //判空
        if(leftTail != null) {
            leftTail.right = pRootOfTree;
            pRootOfTree.left = leftTail;
        }

        //继续转换右子树
        TreeNode right = Convert(pRootOfTree.right);
        //将原树的根节点和转换后的右链表的首节点相连
        if(right != null) {
            right.left = pRootOfTree;
            pRootOfTree.right = right;
        }
        return left == null ? pRootOfTree : left;
    }
}