✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,matlab项目合作可私信。
🍎个人主页:Matlab科研工作室
🍊个人信条:格物致知。
更多Matlab仿真内容点击👇
智能优化算法 神经网络预测 雷达通信 无线传感器
信号处理 图像处理 路径规划 元胞自动机 无人机 电力系统
⛄ 内容介绍
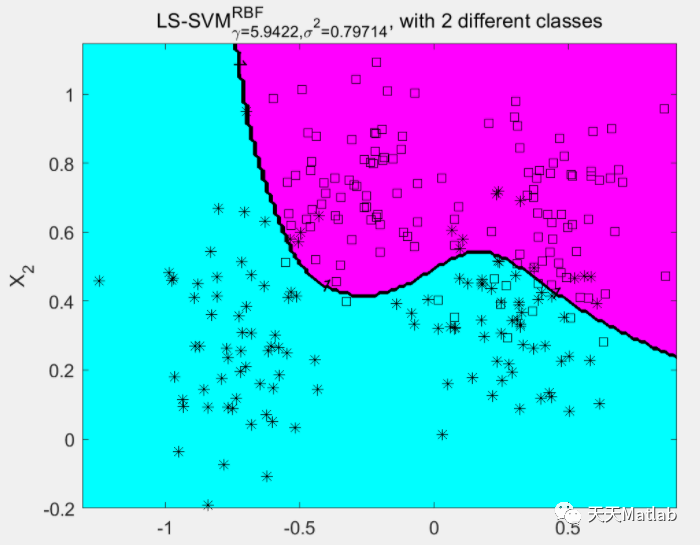
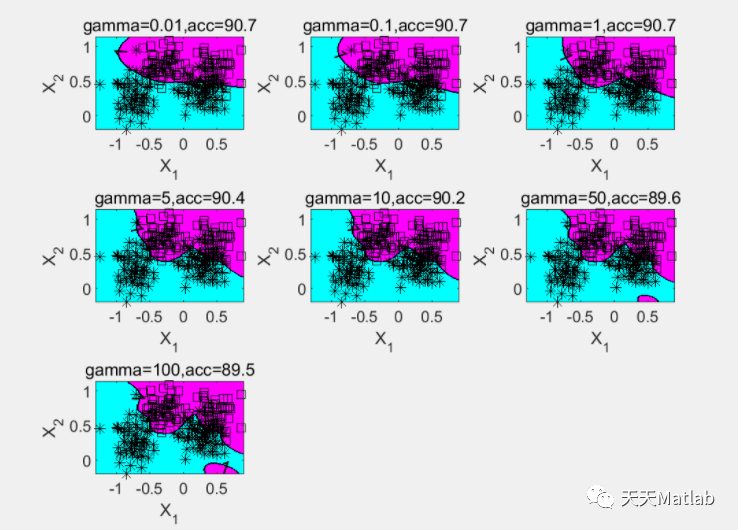
最小二乘支持向量机是支持向量机的一种改进,它是将传统支持向量机中的不等式约束改为等式约束, 且将误差平方和(SumSquaresError)损失函数作为训练集的经验损失,这样就把解二次规划问题转化为求解线性方程组问题, 提高求解问题的速度和收敛精度。
常用的核函数种类:
2、LSSVM工具箱的使用方法
2.1 最小二乘支持向量机Matlab工具箱下载链接:https://www.esat.kuleuven.be/sista/lssvmlab/(毫无疑问下载最新版本)
2.2 将LS-SVM文件添加到matlan使用路径中,便可直接使用。
具体使用步骤:
1 导入训练数据:load 读取mat文件和ASCII文件;xlsread读取.xls文件;csvread读取.csv文件。
2 数据预处理:效果是加快训练速度。
方法有:归一化处理(把每组数据都变为 - 1~ +1之间的数, 所涉及到的函数有premnmx, post mnmx, tramnmx)
标准化处理(把每组数据都化为均值为 0, 方差为 1的一组数据, 所涉及到的函数有 prestd,poatstd, trastd)
主成分分析 (进行正交处理, 减少输入数据的维数, 所涉及到的函数有 prepca, trapca)
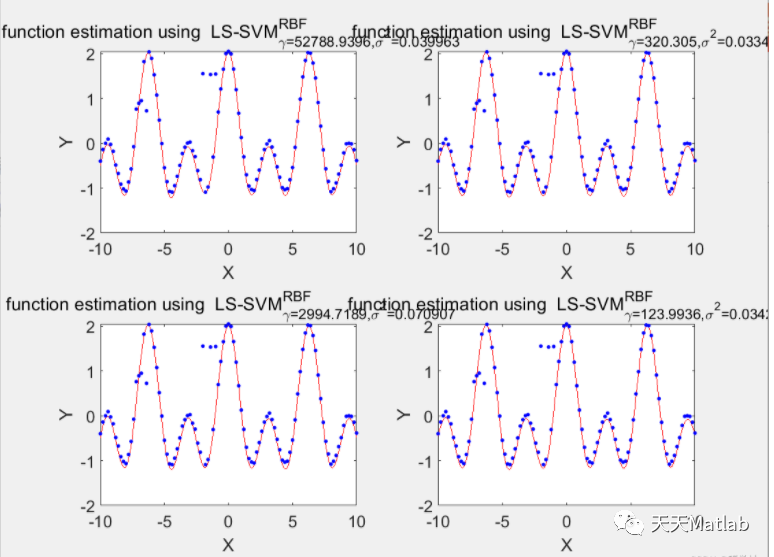
3 LS-SVM lab用于函数回归主要用到 3个函数, trainlssvm函数用来训练建立模型, simlssvm函数用于预估模型, plotlssvm函数是 LS-SVM lab工具箱的专用绘图函数。
⛄ 部分代码
clc;
disp('This is a simple demo, solving a simple regression task using');
disp('LS-SVMlab and constructing confidence intervals. A dataset is constructed in the right formatting. The');
disp('data are represented as matrices where each row contains one');
disp('datapoint: ');
disp(' ');
disp('press <ENTER> key'); pause
disp(' ');
disp('>> X = (-3:0.02:3)'';');
X = (-3:0.02:3)';
disp('>> Y = sinc(X)+0.1.*randn(length(X),1);');
eval('Y = sinc(X)+0.1.*randn(length(X),1);',...
'Y = sin(pi.*X+12345*eps)./(pi*X+12345*eps)+0.1.*randn(length(X),1);');
disp('>> X');
X
disp('>> Y');
Y
disp('In order to make an LS-SVM model, we need 2 extra parameters: gamma');
disp('(gam) is the regularization parameter, determining the trade-off');
disp('between the fitting error minimization and smoothness of the');
disp('estimated function. sigma^2 (sig2) is the kernel function');
disp('parameter of the RBF kernel. These can be found via cross-validation:');
disp(' ');
model = initlssvm(X,Y,'f',[],[],'RBF_kernel','o');
disp('>> model = tunelssvm(model,''simplex'',''crossvalidatelssvm'',{10,''mse''});');
model = tunelssvm(model,'simplex','crossvalidatelssvm',{10,'mse'});
disp(' ');
disp('press <ENTER> key'); pause
disp(' ');
disp('Training the model ');
disp(' ');
disp('>> model = trainlssvm(model)');
model = trainlssvm(model);
disp(' ');
disp('Computation of Confidence Intervals ');
disp(' ');
disp('press <ENTER> key'); pause
disp('ci = cilssvm(model);')
ci = cilssvm(model);
disp('The LS-SVM result and confidence intervals can be displayed if the dimension of the input');
disp('data is 1 or 2. ');
disp(' ');
disp('>> plotlssvm(model);');
figure; plotlssvm(model);
disp(' ');
hold all
fill([X;flipud(X)],[ci(:,1);flipud(ci(:,2))],'c','FaceAlpha',0.5,'EdgeAlpha',1,'EdgeColor','w')
disp('All plotting is done with this simple command. It looks for the');
disp('best way of displaying the result.')
disp(' ');
disp(' This concludes the demo');
⛄ 运行结果
⛄ 参考文献
❤️ 关注我领取海量matlab电子书和数学建模资料
❤️部分理论引用网络文献,若有侵权联系博主删除
基于最小二乘支持向量机(LS-SVM)进行分类、函数估计、时间序列预测和无监督学习附Matlab代码
news2026/2/10 12:34:30
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/12696.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
线性回归(机器学习)
用神经网络的思维来看待线性回归 单层的神经网络,其实就是一个神经元,可以完成一些线性的工作,比如拟合一条直线,这用一个神经元就可以实现。 当变量多于一个时,两个变量的量和数值有可能差别很大,这种情况…
MicroApp的Vite项目,特别全面
目录
前言
简介
分离
修改基座
子应用修改
修改vite.config.js编辑
修改index.html
基座修改
处理子应用静态资源
效果
基座与子应用传值
在基座的MicroApp的index页面修改
在子应用的App.tsx文件进行useEffect的监听
效果编辑
去掉菜单栏头部
效果编辑 …
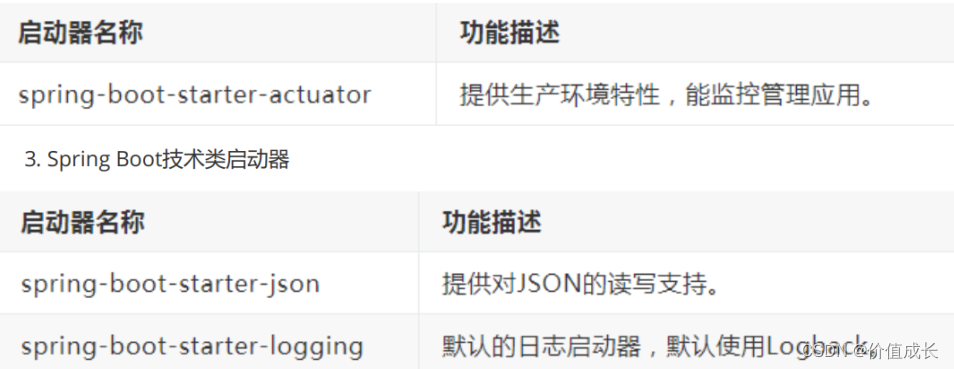
SpringBoot面试
0. Spring Boot 原理 Spring Boot 是由 Pivotal 团队提供的全新框架,其设计目的是用来简化新 Spring 应用的初始搭建以及开发过程。该框架使用了特定的方式来进行配置,从而使开发人员不再需要定义样板化的配置。通过这种方式,Spring Boot 致力…
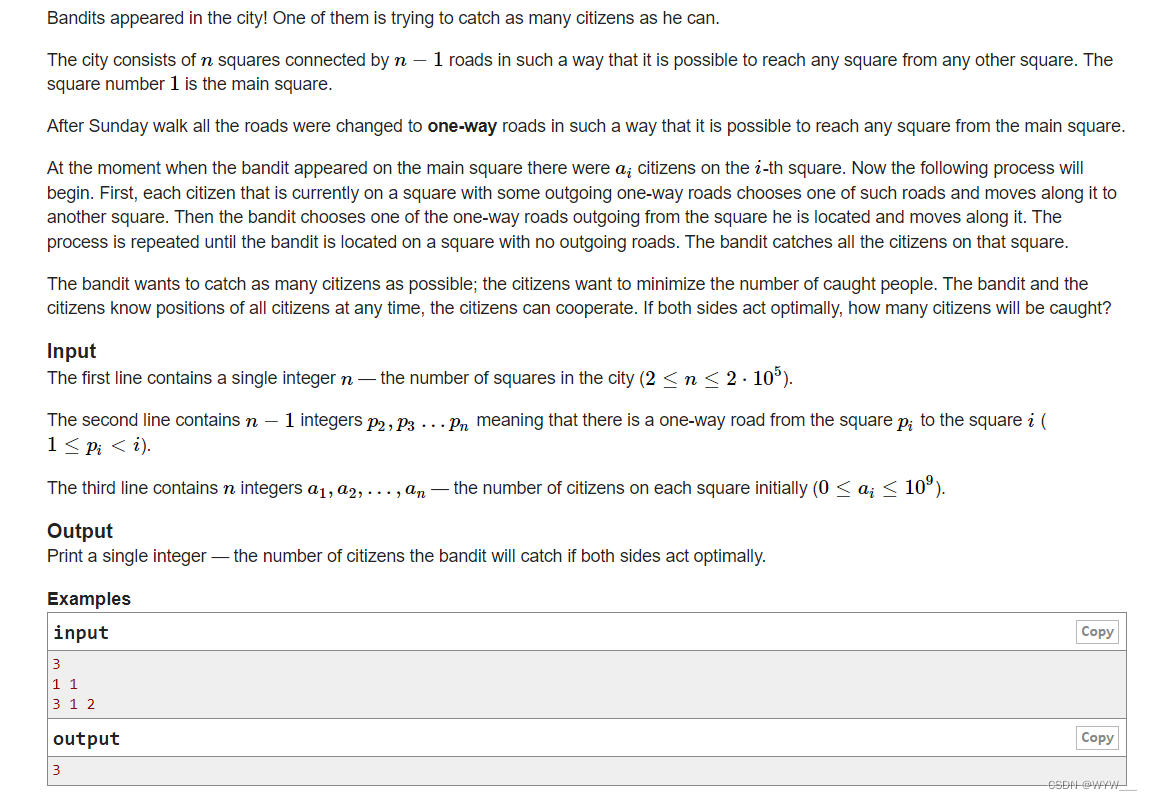
D. Bandit in a City(DFS + 叶子节点数目)
Problem - 1436D - Codeforces 输出标准输出 城市里出现了强盗! 他们中的一个正试图尽可能多地抓捕市民。
这个城市由n个广场组成,由n-1条道路连接,从任何其他广场都可以到达任何广场。1号广场是主广场。
星期天散步后,所有的道路都改为单行…
uni-app —— 小程序登录功能的相关实现
文章目录 前言一、示例图二、静态页面的搭建 1.登录页面的静态页面css样式设置2.我的页面的静态页面css样式设置三、登录页面的实现逻辑 1.进行表单验证的组件2.验证登录成功的思路3.具体代码实现一、示例图 二、静态页面的搭建
实现思路: 主要需要实现的功能点&am…
企业为什么做不好生产计划?
生产计划是企业对生产任务作出统筹安排,具体拟定生产产品的品种、数量、质量和进度的计划。是企业经营计划的重要组成部分,是企业进行生产管理的重要依据。既是实现企业经营目标的重要手段,也是组织和指导企业生产活动有计划进行的依据。企业…
【微服务】SpringCloud微服务注册源码解析
目录
一、前言
1、简述
2、SpringCloudCommons 项目
二、客户端服务注册
1、流程图
2、入口
2.1、客户端注册引入依赖
3、EurekaServiceRegistry服务注册机
3.1、EurekaServiceRegistry注册逻辑
4、ApplicationInfoManager
4.1、setInstanceStatus(InstanceStatus s…
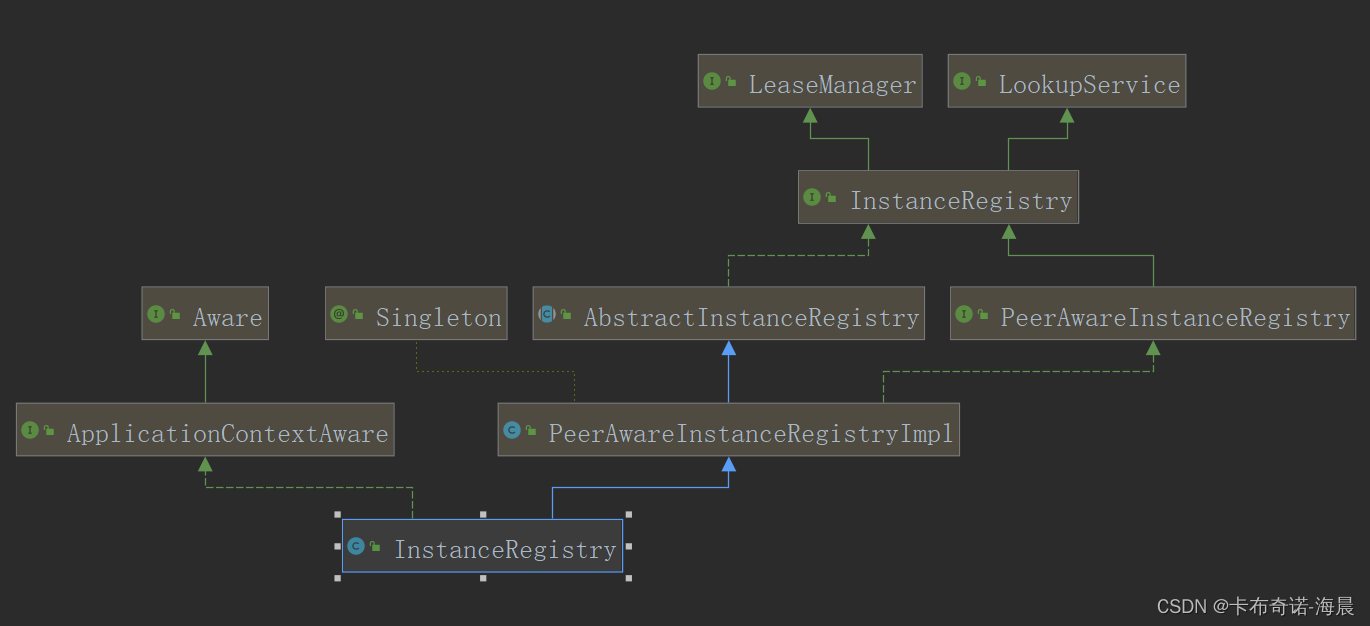
【区块链技术与应用】(七)
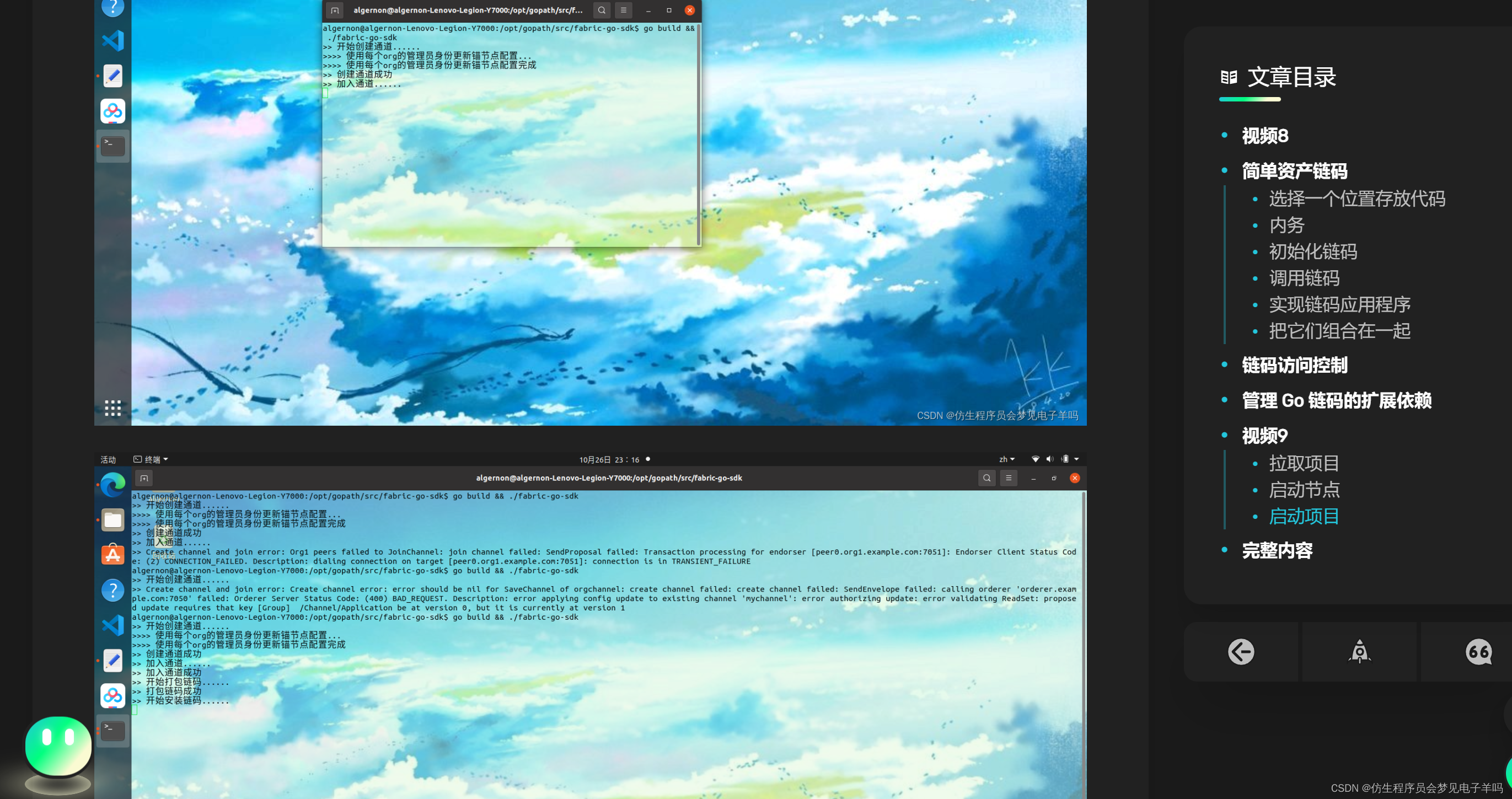
资料来源 https://pkg.go.dev/github.com/hyperledger/fabric-sdk-go#section-readme https://github.com/hyperledger/fabric-sdk-go https://wiki.hyperledger.org/display/fabric https://github.com/hyperledger/fabric-samples 书接上回,补充getway链码分析
上…
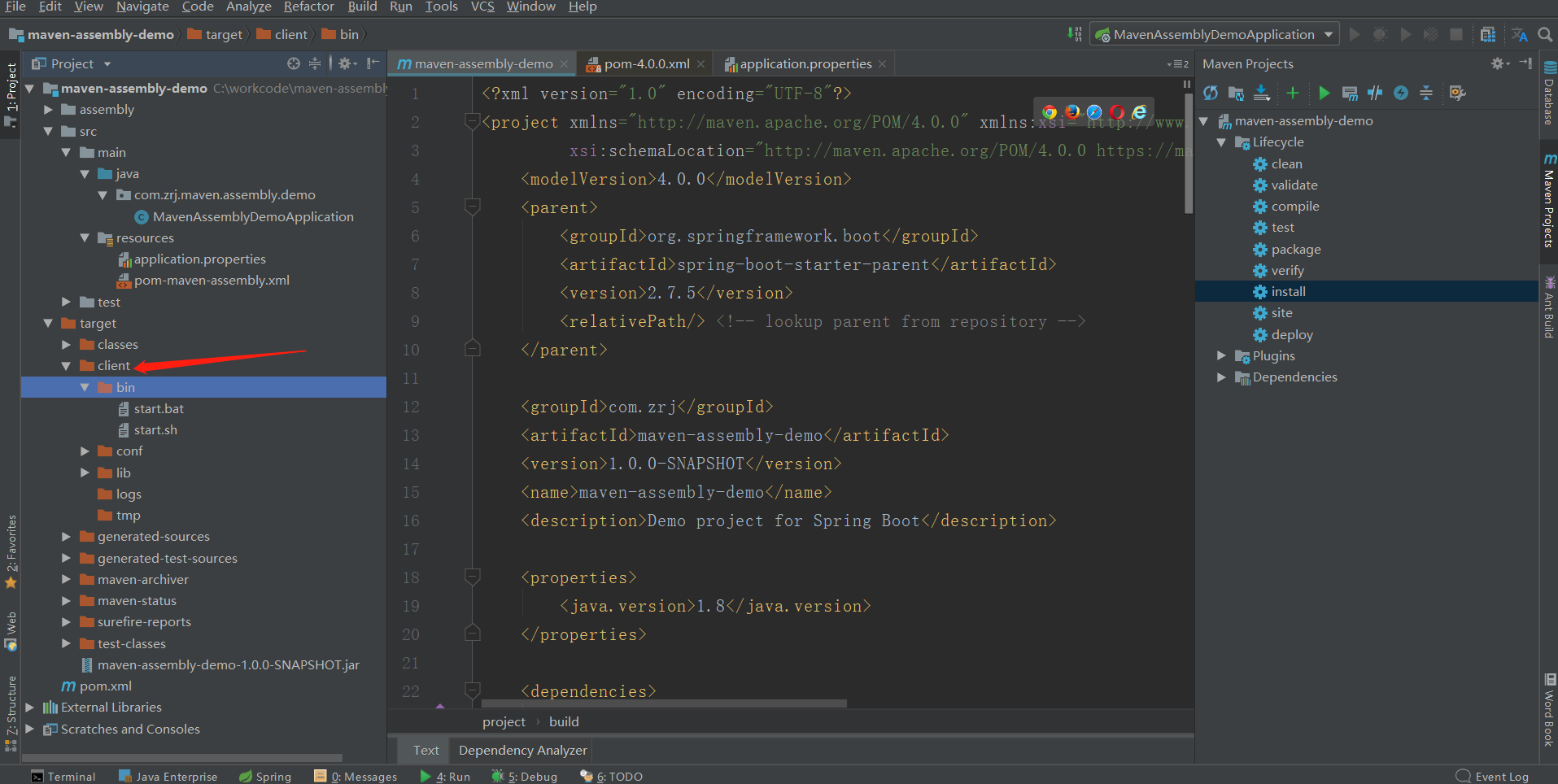
maven assembly打包生成Java应用启动脚本bat和sh
1. maven插件介绍
springboot应用通过maven插件appassembler-maven-plugi生成启动脚本bat和sh。根据官网介绍,这个插件主要用于生成启动 java应用程序的脚本,能将项目依赖jar能够打包目录中,并且它们加入启动脚本类路径中。
主要命令 appas…
springboot瑞吉外卖
创建数据库,项目初始化静态资源不在static目录下,如何映射结果类登录过滤器拦截路径全局异常处理器分页查询消息转换器修改禁用分页编辑公共字段自动填充使用ThreadLocal新增用户绑定的数据不可删除上传下载前端传递的数据,不在同一张表时,DT…
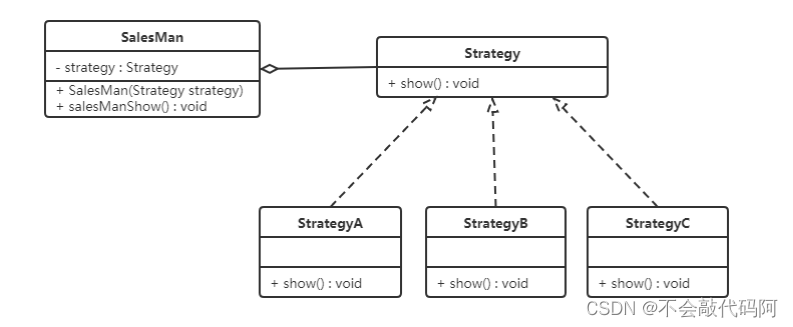
java设计模式之策略模式
一:策略模式
1.什么是策略模式? 模板方法模式是一种行为设计模式, 它在超类中定义了一个算法的框架, 允许子类在不修改结构的情况下重写算法的特定步骤。 策略模式的基本介绍 1.策略模式(Strategy Pattern)中&#x…
【MQ基本概念 MQ的工作原理】
一、MQ基本概念 1、MQ概述 MQ全称Message Queue(消息队列),是在消息的传输过程中保存 消息的容器。多用于分布式系统之间进 行通信。 小结 MQ,消息 队列,存储消息的中间件 分布式系统通信两种方式:直接远程…
2022年数维杯D题 极端天气问题思路指导
D题损失评估与应对策略的研究三重拉尼娜事件下的极端气候灾害
很明显D题是一个数据收集➕数据处理类型题目,这与美赛中的E题题型相似。该题所涉及的极端天气与2021年小美赛极端天气题目高度相似。因此,我们首先对大家整理了去年小美赛极端天气的相关论文…
Kubeadm搭建kubernetes集群
Kubeadm搭建kubernetes集群
环境说明 | 角色 | ip | 操作系统 |组件 | | – | – | – | | master | 192.168.226.10 |centos8 | docker,kubectl,kubeadm,kubelet | | node1 | 192.168.226.20 |centos8 |docker,kubectlÿ…
【Hack The Box】windows练习-- Blackfield
HTB 学习笔记
【Hack The Box】windows练习-- Blackfield 🔥系列专栏:Hack The Box 🎉欢迎关注🔎点赞👍收藏⭐️留言📝 📆首发时间:🌴2022年11月17日🌴 &…
[Games 101] Lecture 10 Geometry 1 (Introduction)
Geometry 1 (Introduction)
Ways to Represent Geometry
隐式 (Implicit) 几何
只告诉点满足某种约束或关系,并不给出实际的点,也就是说,定义 f(x,y,z)0f(x,y,z) 0 f(x,y,z)0
例如,定义三维空间中的点,满足&#…
上海亚商投顾:信创概念掀涨停潮
上海亚商投顾前言:无惧大盘大跌,解密龙虎榜资金,跟踪一线游资和机构资金动向,识别短期热点和强势个股。 市场情绪指数早盘低开低走,沪指一度跌超1%,失守3100点关口,创业板指盘中跌逾2%ÿ…
软件工程毕业设计 SSM计算机毕设项目合集【源码+论文】
文章目录前言 题目1 : 基于SSM的网上租车系统 <br /> 题目2 : 基于SSM的药品管理系统 <br /> 题目3 : 基于SSM的药源药品商城保健品购物网站 <br /> 题目4 : 基于SSM的疫情防控物业管理系统 <br /> 题目5 : 基于SSM的音乐网站 <br />前言
&…
如何通过更好的文档管理减轻小型企业的压力
如何通过更好的文档管理减轻小型企业的压力
企业如何处理企业文档在很大程度上体现了企业以目前的形式茁壮成长的能力以及在当今的市场中成长为成熟的、有竞争力的实体的能力。
具体来说,在小型企业中,许多员工都需要承担多种职责,每一分钟…






![[Games 101] Lecture 10 Geometry 1 (Introduction)](https://img-blog.csdnimg.cn/img_convert/e6245309a23812900e2b5aa87e2fc004.png)