用神经网络的思维来看待线性回归

---

        单层的神经网络，其实就是一个神经元，可以完成一些线性的工作，比如拟合一条直线，这用一个神经元就可以实现。

        当变量多于一个时，两个变量的量和数值有可能差别很大，这种情况下，我们通常需要对样本特征数据做归一化，然后把数据喂给神经网络进行训练。

一元线性回归模型

---

回归分析是一种数学模型。当因变量和自变量为线性关系时，它是一种特殊的线性模型。

最简单的情形是一元线性回归，由大体上有线性关系的一个自变量和一个因变量组成，模型是：

 

 

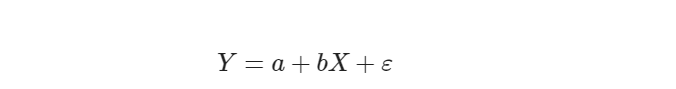
X 是自变量，Y 是因变量，ε 是随机误差，a 和 b 是参数，在线性回归模型中，a,b 是我们要通过算法学习出来的。

公式： 

 

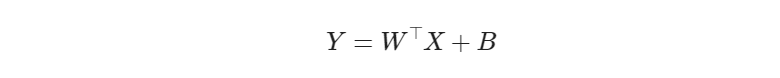
线性回归问题

---

我们接下来会用几种方法来解决这个问题：

1. 最小二乘法；
2. 梯度下降法；
3. 简单的神经网络法；
4. 更通用的神经网络算法；

 这三者的主要区别是样本数据 X 的形状定义，相应地会影响到 W 的形状定义。

最小二乘法

---

1、线性特性

所谓线性特性，是指估计量分别是样本观测值的线性函数，亦即估计量和观测值的线性组合 。

2、无偏性

无偏性，是指参数估计量的期望值分别等于总体真实参数  。

3、最小方差性

所谓最小方差性，是指估计量与用其它方法求得的估计量比较，其方差最小，即最佳。最小方差性又称有效性。这一性质就是著名的高斯一马尔可夫（ Gauss-Markov）定理。这个定理阐明了普通最小二乘估计量与用其它方法求得的任何线性无偏估计量相比，它是最佳的 [10]  。

代码实现

---

计算W值 

# method1
def method1(X,Y,m):
    x_mean = X.mean()
    p = sum(Y*(X-x_mean))
    q = sum(X*X) - sum(X)*sum(X)/m
    w = p/q
    return w

# method2
def method2(X,Y,m):
    x_mean = X.mean()
    y_mean = Y.mean()
    p = sum(X*(Y-y_mean))
    q = sum(X*X) - x_mean*sum(X)
    w = p/q
    return w

# method3
def method3(X,Y,m):
    p = m*sum(X*Y) - sum(X)*sum(Y)
    q = m*sum(X*X) - sum(X)*sum(X)
    w = p/q
    return w

计算b值

# calculate_b_1
def calculate_b_1(X,Y,w,m):
    b = sum(Y-w*X)/m
    return b

# calculate_b_2
def calculate_b_2(X,Y,w):
    b = Y.mean() - w * X.mean()
    return b

梯度下降法

---

数学原理

线性函数：

 

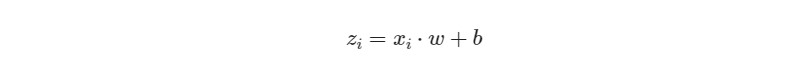
损失函数（Loss Function）：

 

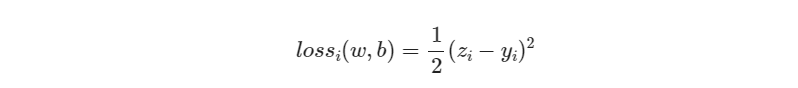
梯度下降法和最小二乘法的模型及损失函数是相同的

都是一个线性模型加均方差损失函数，模型用于拟合，损失函数用于评估效果。

两者的区别在于：最小二乘法从损失函数求导，直接求得数学解析解，而梯度下降以及后面的神经网络，都是利用导数传递误差，再通过迭代方式一步一步（用近似解）逼近真实解。

梯度下降法代码的实现

---

if __name__ == '__main__':

    reader = SimpleDataReader()
    reader.ReadData()
    X,Y = reader.GetWholeTrainSamples()

    eta = 0.1
    w, b = 0.0, 0.0
    for i in range(reader.num_train):
        # get x and y value for one sample
        xi = X[i]
        yi = Y[i]
        # 公式1
        zi = xi * w + b
        # 公式3
        dz = zi - yi
        # 公式4
        dw = dz * xi
        # 公式5
        db = dz
        # update w,b
        w = w - eta * dw
        b = b - eta * db

    print("w=", w)    
    print("b=", b)

神经网络法

---

神经网络做线性拟合的原理，即：

1. 初始化权重值
2. 根据权重值放出一个解
3. 根据均方差函数求误差
4. 误差反向传播给线性计算部分以调整权重值
5. 是否满足终止条件？不满足的话跳回2

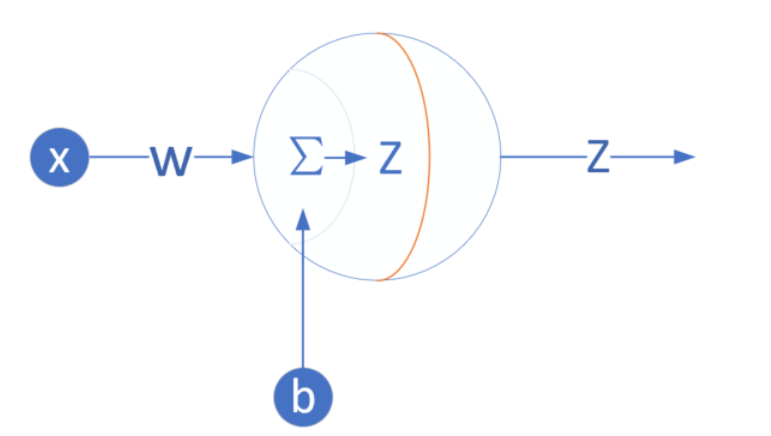
 输入层

---

 神经元在输入层的输入特征

权重 w,b

---

一元线性问题，所以 w,b 都是标量。

输出层

---

输出层 1 个神经元，线性预测公式是：

zi = xi ⋅ w + b

z 是模型的预测输出，y 是实际的样本标签值，下标 i 为样本。

 反向传播

---

 

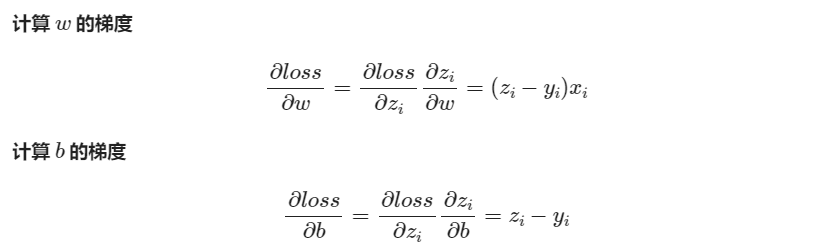
定义类

class NeuralNet(object):
    def __init__(self, eta):
        self.eta = eta
        self.w = 0
        self.b = 0

前向计算

def __forward(self, x):
    z = x * self.w + self.b
    return z

反向传播

def __backward(self, x,y,z):
        dz = z - y
        db = dz
        dw = x * dz
        return dw, db

梯度更新

def __update(self, dw, db):
        self.w = self.w - self.eta * dw
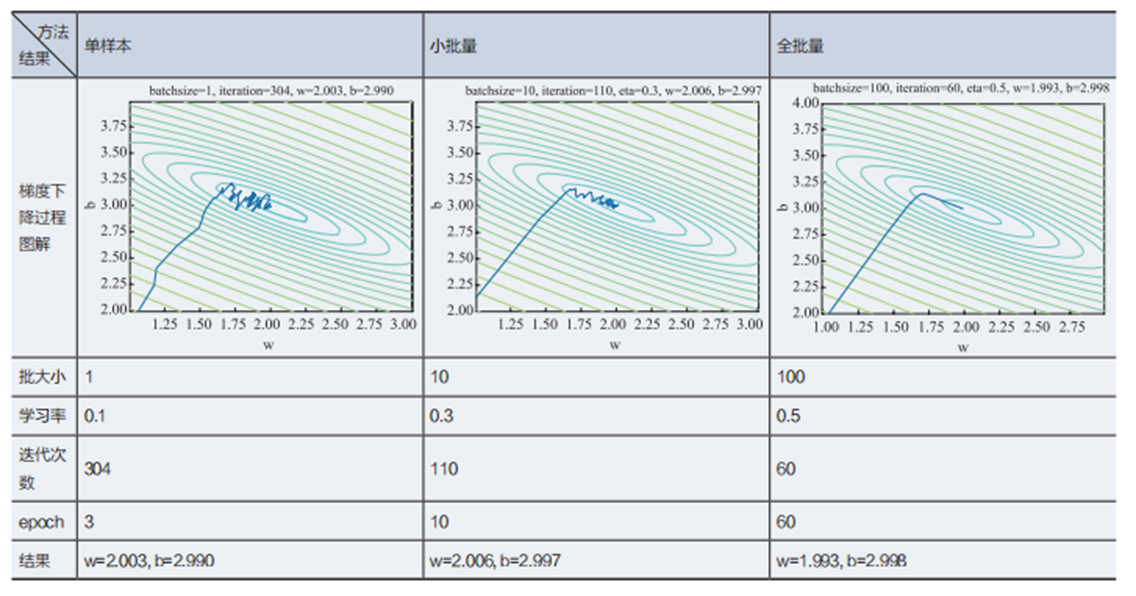
        self.b = self.b - self.eta * db

梯度下降的三种形式

---

单样本随机梯度下降、小批量样本梯度下降、全批量样本梯度下降