Geometry 1 (Introduction)

Ways to Represent Geometry

隐式 (Implicit) 几何

• 只告诉点满足某种约束或关系，并不给出实际的点，也就是说，定义

$$f(x,y,z)=0$$

• 例如，定义三维空间中的点，满足，$x^2+y^2+z^2=1$
• 判断一个面有哪些点是困难的，判断一个点与面的位置关系是容易的

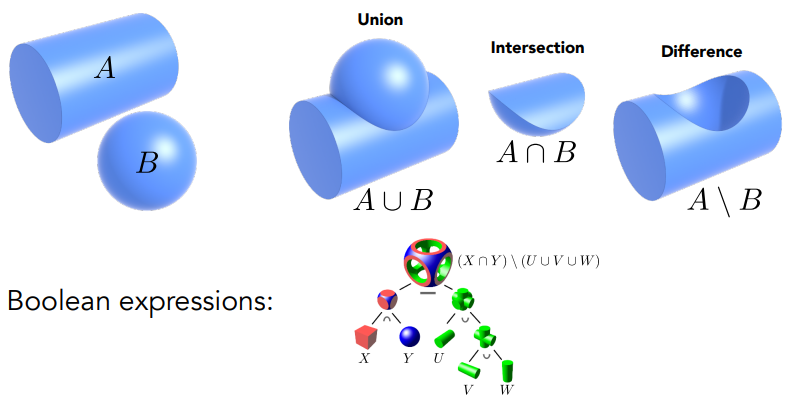
Constructive Solid Geometry

使用布尔运算拼接基本几何体

Distance Functions

对于任何一个几何，不描述它的表面，描述空间中的任何一个点到这个表面的任意点最近距离（可以是正的或者负的）

Level Set Methods

找到 $f(x)=0$ 的曲线就是物体的边界

Fractals 分形

自相似，自己和自己的某个部分非常像

Implicit Representations‘ Pros & Cons

Pros：

• compact description (e.g., a function)
• certain queries easy (inside object, distance to surface)
• good for ray-to-surface intersection (more later) ：和光线求交容易
• for simple shapes, exact description / no sampling error
• easy to handle changes in topology (e.g., fluid)

Cons:

• difficult to model complex shapes

显式 (Explicit) 几何

• 通过参数映射的方式定义空间中的点

$$f:{\mathbb{R}}^2\to {\mathbb{R}}^3;(u,v)\mapsto (x,y,z)$$

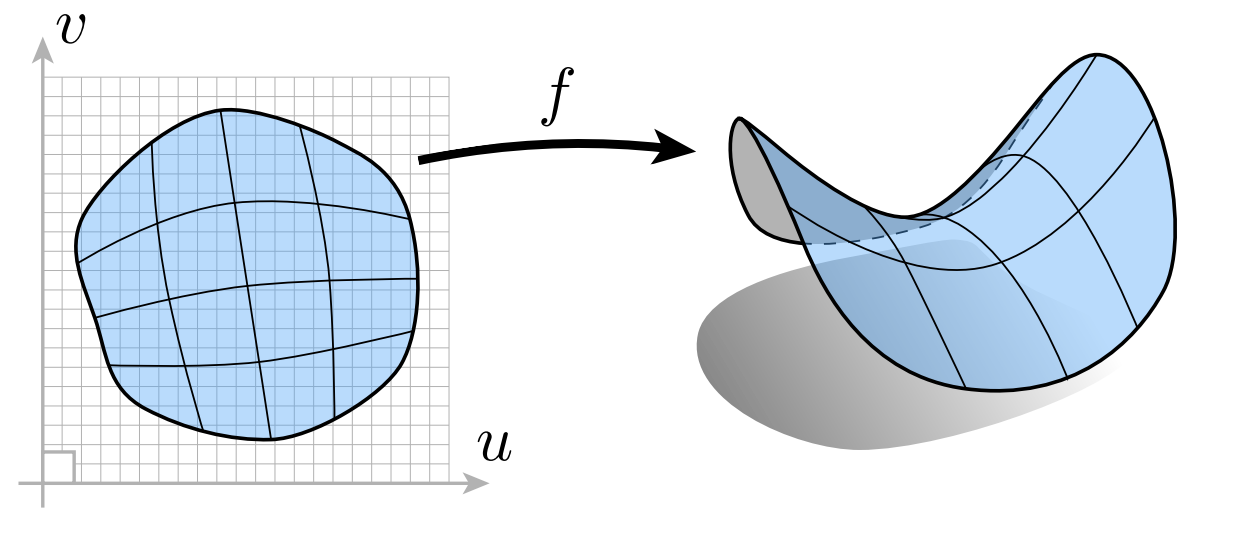
• 判断一个面有哪些点是容易的，判断一个点与面的位置关系是困难的

Point Cloud 点云

• 使用 $(x,y,z)$ 的列表表示点
• 经常需要将点云转化成三角形面

Polygon Mesh

• 使用多边形（尤其是三角形存储）
• 在图形学中得到最广泛应用的显式表示

The Wavefront Object File (.obj) Format

• 描述空间中的点、法线、材质、坐标、连接关系的文本文件