论文信息

论文地址：https://arxiv.org/pdf/2210.17168.pdf

Abstract

论文提出了一种token-level的自蒸馏对比学习(self-distillation contrastive learning)方法。

1. Introduction

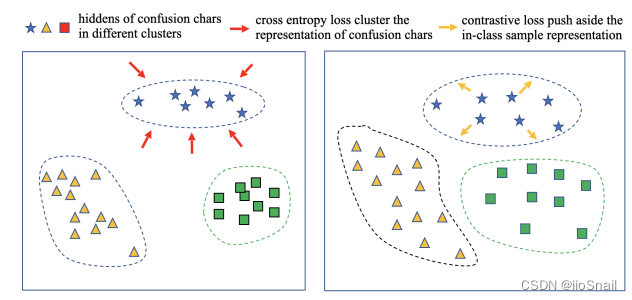
传统方法使用BERT后，会对confusion chars进行聚类，但使用作者提出的方法，会让其变得分布更均匀。

confusion chars: 指的应该是易出错的字。

2. Methodology

2.1 The Main Model

作者提取特征的方式：① 先用MacBERT得到hidden states，然后用word embedding和hidden states进行点乘。写成公式为：

$$\mathbf{H}=\mathbf{MacBERT}(\mathbf{X})\cdot \mathbf{W}$$

这里的 $W$ 应该就是BERT最前面的embedding层对X编码后的向量。

后面就是正常接个输出层再计算CrossEntropyLoss

2.2 Contrastive Loss

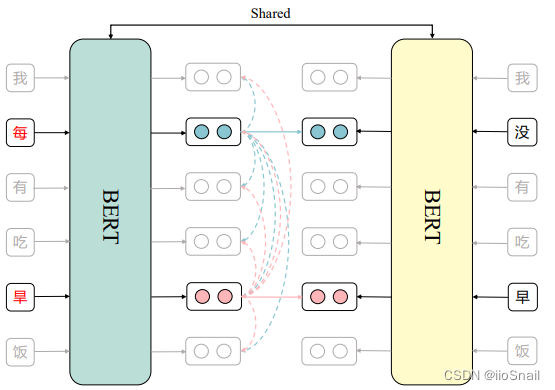
基本思路：让错字token的特征向量和其对应正确字的token特征向量距离越近越好。这样BERT就能拿着错字，然后编码出对应正确字的向量，最后的预测层就能预测对了。

作者的做法：

1. 错误句子从左边进入BERT，正确句子从右边进入BERT
2. 对于错字，进行对比学习，让其与对应的正确字的特征向量距离越近越好。即每这个错字的正样本为没。
3. 将错误句子的其他token作为错字的负样本，使错字token的特征向量与其他向量的距离越远越好。上图中，每字有5个负样本，即我、有、吃、旱、饭

上图中双头实线(↔)表示这两个token要距离越近越好，双头虚线表示这两个token要距离越远越好

损失函数公式如下：

$$L_c=-\sum _{i=1}^n\mathbb{L}\left({\tilde{x}}_i\right)\log \frac{\exp \left(\mathrm{sim}\left({\tilde{h}}_i,h_i\right)/\tau \right)}{{\sum }_{j=1}^n\exp \left(\mathrm{sim}\left({\tilde{h}}_i,h_j\right)/\tau \right)}$$

其中：

• $n$ : 为n个token
• $\mathbb{L}\left({\tilde{x}}_i\right)$: 当 $x_i$为错字时，$\mathbb{L}\left({\tilde{x}}_i\right)=1$，否则为 $0$。即只算错字的损失。
• $\text{sim}(\cdot )$：余弦相似度函数
• ${\tilde{h}}_i$: 正确句子(右边BERT)输出的token的特征向量
• $h_i$：错误句子(左边BERT)输出的token的特征向量
• $\tau$：温度超参

上面损失使用CrossEntropyLoss实现。

作者还为右边的BERT增加了一个Loss $L_y$，目的是让右边可以输出它的输入，即copy-paste任务。

最终的损失如下：

$$L=L_x+\alpha L_y+\beta L_c$$

2.3 Implementation Details(Hyperparameters)

• BERT：MacBERT
• optimizer: AdamW
• 学习率: 7e-5
• batch_size: 48
• $\lambda$: 0.9 （TODO，作者说的这个lambda不知道是啥）
• $\alpha$: 1
• $\beta$: 0.5
• $\tau$: 0.9
• epoch: 20次

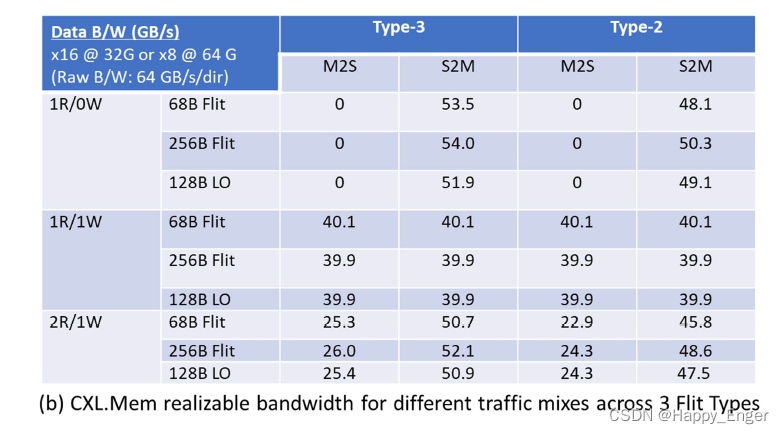
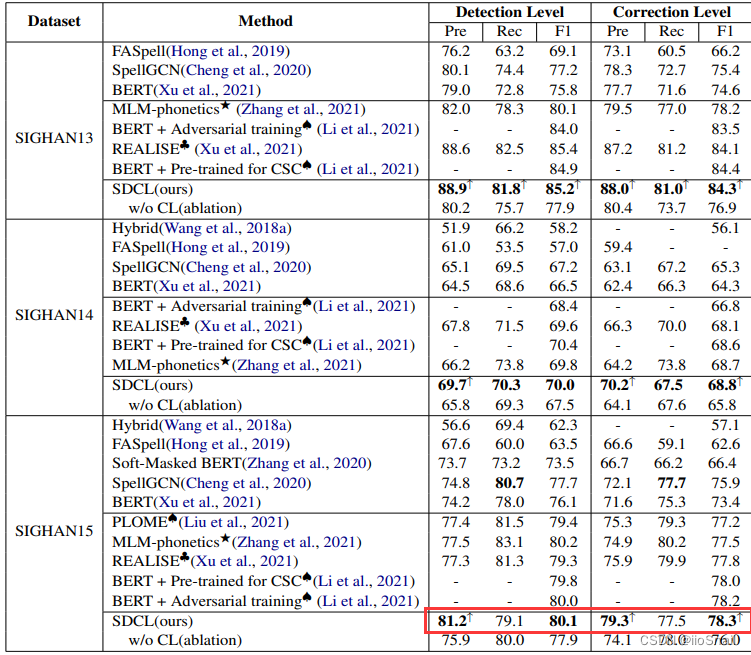
3. Experiments

代码实现

import torch
import torch.nn as nn
from transformers import BertTokenizerFast, BertForMaskedLM
import torch.nn.functional as F


class SDCLModel(nn.Module):

    def __init__(self):
        super(SDCLModel, self).__init__()
        self.tokenizer = BertTokenizerFast.from_pretrained('hfl/chinese-macbert-base')
        self.model = BertForMaskedLM.from_pretrained('hfl/chinese-macbert-base')

        self.alpha = 1
        self.beta = 0.5
        self.temperature = 0.9

    def forward(self, inputs, targets=None):
    	"""
    	inputs: 为tokenizer对原文本编码后的输入，包括input_ids, attention_mask等
    	targets：与inputs相同，只不过是对目标文本编码后的结果。
    	"""
        if targets is not None:
        	# 提取labels的input_ids
            text_labels = targets['input_ids'].clone()
            text_labels[text_labels == 0] = -100  # -100计算损失时会忽略
        else:
            text_labels = None
		
        word_embeddings = self.model.bert.embeddings.word_embeddings(inputs['input_ids'])
        hidden_states = self.model.bert(**inputs).last_hidden_state
        logits = self.model.cls(hidden_states * word_embeddings)

        if targets:
            loss = F.cross_entropy(logits.view(logits.shape[0] * logits.shape[1], logits.shape[2]), text_labels.view(-1))
        else:
            loss = 0.

        return logits, hidden_states, loss

    def extract_outputs(self, outputs):
        logits, _, _ = outputs
        return logits.argmax(-1)

    def compute_loss(self, outputs, targets, inputs, detect_targets, *args, **kwargs):
        logits_x, hidden_states_x, loss_x = outputs
        logits_y, hidden_states_y, loss_y = self.forward(targets, targets)

        # FIXME
        anchor_samples = hidden_states_x[detect_targets.bool()]
        positive_samples = hidden_states_y[detect_targets.bool()]
        negative_samples = hidden_states_x[~detect_targets.bool() & inputs['attention_mask'].bool()]

        # 错字和对应正确的字计算余弦相似度
        positive_sim = F.cosine_similarity(anchor_samples, positive_samples)
        # 错字与所有batch内的所有其他字计算余弦相似度
        # （FIXME，这里与原论文不一致，原论文说的是与当前句子的其他字计算，但我除了for循环，不知道该怎么写）
        negative_sim = F.cosine_similarity(anchor_samples.unsqueeze(1), negative_samples.unsqueeze(0), dim=-1)

        sims = torch.concat([positive_sim.unsqueeze(1), negative_sim], dim=1) / self.temperature
        sim_labels = torch.zeros(sims.shape[0]).long().to(self.args.device)

        loss_c = F.cross_entropy(sims, sim_labels)

        self.loss_c = float(loss_c)  # 记录一下

        return loss_x + self.alpha * loss_y + self.beta * loss_c

    def get_optimizer(self):
        return torch.optim.AdamW(self.parameters(), lr=7e-5)

    def predict(self, src):
        src = ' '.join(src.replace(" ", ""))
        inputs = self.tokenizer(src, return_tensors='pt').to(self.args.device)
        outputs = self.forward(inputs)
        outputs = self.extract_outputs(outputs)[0][1:-1]
        return self.tokenizer.decode(outputs).replace(' ', '')

个人总结

值得借鉴的地方

1. 作者并没有直接使用BERT的输出作为token embedding，而是使用点乘的方式融合了BERT的输出和word embeddings