一、向量的点乘

向量的点乘（dot）是一个标量积，也叫向量的内积、数量积。

点乘公式：

有向量a b

a=(a1,a2,a3,...,an)

b=(b1,b2,b3,...,bn);

那么向量a(dot)b=a1b1+a2b2+a3b3+....+anbn

从上面我们能可以看出，点乘得到的结果只是一个数值

注意：点乘的基础是两个向量有相同的维度

 点乘的几何意义

几何意义：一个向量在另外一个向量上的投影，也可以计算出两个向量之间夹角

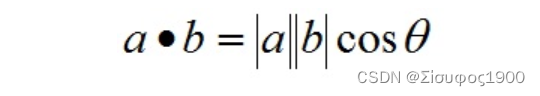
 余弦定理：

点乘推导过程：

 因此：

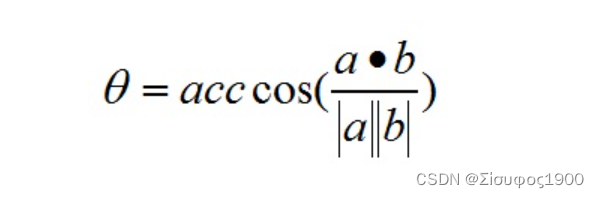
 性质：

1. a⋅b>0则方向基本相同，夹角在0°到90°之间
2. a⋅b=0则正交，相互垂直
3. a⋅b<0则方向基本相反，夹角在90°到180°之间

二、向量的叉乘

向量的叉乘是一个向量积，我们也经常称之为向量叉乘积或者外积

在空间中有两个向量： a=(x1,y1,z1) ， b=(x2,y2,z2)， a 与 b之间夹角为 θ。

从代数角度计算：

a×b=(y1z2−z1y2,z1x2−x1z2,x1y2−y1x2)

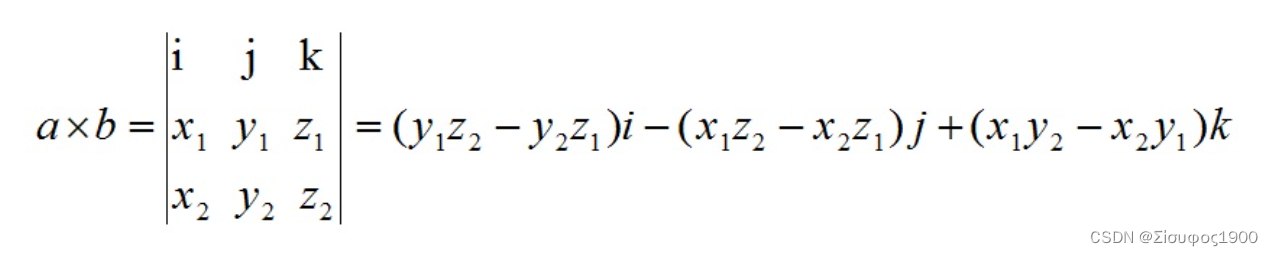
 其中i=(1,0,0),j=(0,1,0),k=(0,0,1);

几何意义：

在三维几何中，向量a和向量b的叉乘结果是一个向量，更为熟知的叫法是法向量，该向量垂直于a和b向量构成的平面。

 

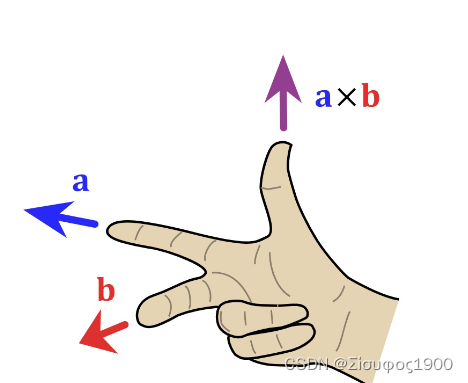
a×b=|a||b|sin⁡θ

性质:

1、a×b=-b×a

2、a×a=0

3、a×（b×c）=a×b+a×c