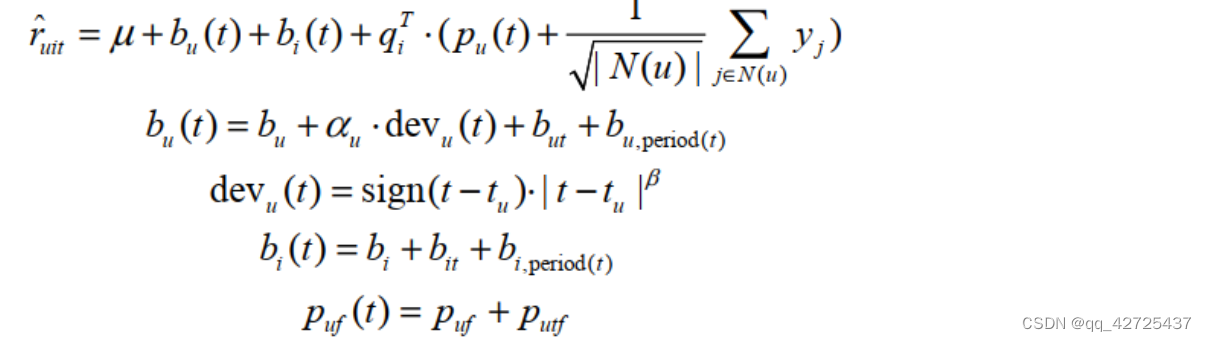SVD recommendation systems
为什么在推荐系统中使用SVD
一个好的推荐系统一定有小的RMSE
R
M
S
E
=
1
m
∑
i
=
1
m
(
Y
i
−
f
(
x
i
)
2
RMSE = \sqrt{\frac{1}{m} \sum_{i=1}^m(Y_i-f(x_i)^2}
RMSE=m1i=1∑m(Yi−f(xi)2
希望模型能够在已知的ratings上有好的结果的同时,也希望在未知ratings上能够表现很好(比如用户还没有见过一部电影)。ratings的意思见:GLOCAL-K
假设有m个items,n个users,我们可以对rating matrix R进行近似,这里R有m行,n列
R
≈
Q
⋅
P
T
R \approx Q \cdot P^T
R≈Q⋅PT
其中Q为mk,P^T为kn,这个可以理解为隐空间是k维。
这样我们就可以利用Q和P去预测R中的缺失值。
r
^
x
i
=
q
i
⋅
p
x
T
=
∑
f
q
i
f
⋅
p
x
f
\hat{r}_{xi} = q_i \cdot p_x^T = \sum_fq_{if} \cdot p_{xf}
r^xi=qi⋅pxT=f∑qif⋅pxf
SVD的介绍SVD
在这里
A
=
R
,
Q
=
U
,
P
T
=
Σ
V
T
A = R,\\ Q=U,\\ P^T=\Sigma V^T
A=R,Q=U,PT=ΣVT
我们知道SVD可以得到最小的重建损失(Sum of Squared Errors):
min
U
,
V
,
Σ
∑
i
,
j
∈
A
(
A
i
j
−
[
U
Σ
V
T
]
i
j
)
2
\min_{U,V,\Sigma}\sum_{i,j\in A}(A_{ij}-[U\Sigma V^T]_{ij})^2
U,V,Σmini,j∈A∑(Aij−[UΣVT]ij)2
- SSE和RMSE是相关的
R M S E = 1 c S S E RMSE = \frac{1}{c}\sqrt{SSE} RMSE=c1SSE
也就是说SVD也最小化RMSE - 但是SVD是所有entrys的,目前R是有缺失值,所以做出改变。
目标函数:
m i n P , Q ∑ ( i , x ) ∈ R ( r x i − q i ⋅ p x T ) 2 min_{P,Q}\sum_{(i,x)\in R}(r_{xi}-q_i \cdot p^T_x)^2 minP,Q(i,x)∈R∑(rxi−qi⋅pxT)2
防止过拟合,需要正则化
m i n P , Q ∑ ( i , x ) ∈ R ( r x i − q i ⋅ p x T ) 2 + λ [ ∑ x ∣ ∣ p x ∣ ∣ 2 + ∑ i ∣ ∣ q i ∣ ∣ 2 ] min_{P,Q}\sum_{(i,x)\in R}(r_{xi}-q_i \cdot p^T_x)^2+\lambda [\sum_x||p_x||^2+\sum_i||q_i||^2] minP,Q(i,x)∈R∑(rxi−qi⋅pxT)2+λ[x∑∣∣px∣∣2+i∑∣∣qi∣∣2]
增加偏执的SVD
每个人都有自己的打分准则,有的人打分就很高,有的人打分偏低,同样的像一些经典电影就会有很高的评分,所以需要增加偏置来解决这个问题。
r
^
u
i
=
μ
+
b
i
+
b
u
+
p
u
⋅
q
i
T
\hat{r}_{ui} = \mu + b_i+ b_u+p_u \cdot q_i^T
r^ui=μ+bi+bu+pu⋅qiT
其中,
μ
\mu
μ表示全局均值,bu表示用户偏见,bi表示物品偏见。
如果一个用户比网站全局评分小0.5分,那么bu=-0.5,u=3.5,泰坦尼克号的平均分比全局平均分要高1分bi=1.
SVD++
最特别的是加了隐式反馈,不仅考虑评分值,还考虑用户对哪些电影进行了评分,1表示评分,0表示未评分
r
^
u
i
=
μ
+
b
i
+
b
u
+
(
p
u
+
∣
N
(
u
)
∣
−
0.5
∑
i
∈
N
(
u
)
y
i
)
⋅
q
i
T
\hat{r}_{ui} = \mu + b_i+ b_u+(p_u+|N(u)|^{-0.5}\sum_{i \in {N(u)}}y_i) \cdot q_i^T
r^ui=μ+bi+bu+(pu+∣N(u)∣−0.5i∈N(u)∑yi)⋅qiT
其中
∣
N
(
u
)
∣
|N(u)|
∣N(u)∣表示行为物品集,y_j表示物品j所表达的隐式反馈。
timeSVD++
增加了时间的考虑,因为对电影的喜爱会根据时间变化,同时一个电影也会随着时间变化,变得更受欢迎或不受欢迎。