单结晶体管
- 单结晶体管的结构和等效电路
- 工作原理和特性曲线
- 应用举例
单结晶体管的结构和等效电路
在一个低掺杂的N型硅棒上利用扩散工艺形成一个高掺杂P区,在P区与N区接触面形成PN结,就构成单结晶体管(UJT)。其结构示意图如下图所示。

P型半导体引出的电极为发射极e;N型半导体的两端引出两个电极,分别为基极
b
1
b\tiny 1
b1和基极
b
2
b\tiny 2
b2。单结晶体管因有两个基极,故也称为双基极晶体管。其符号如下图所示。

单结晶体管的等效电路图如下图所示,发射极所接P区与N型硅棒形成的PN结等效为二极管D;N型硅棒因掺杂浓度很低而呈现高电阻,二极管阴极与基极
b
2
b\tiny 2
b2之间的等效电阻为
r
b
2
\large r\tiny b2
rb2,与基极
b
1
b\tiny 1
b1之间的等效电阻为
r
b
1
\large r\tiny b1
rb1;
r
b
1
\large r\tiny b1
rb1的阻值受e -
b
1
b\tiny 1
b1间电压的控制,所以等效为可变电阻。

工作原理和特性曲线
单结集体管的发射极电流
i
E
i\tiny E
iE和e -
b
1
b\tiny 1
b1间电压
u
E
B
1
{\large u}{\tiny EB1}
uEB1的关系曲线称为特性曲线。特性曲线的测试电路如下图所示,虚线框内为单结晶体管的等效电路。

当
b
2
b\tiny 2
b2 -
b
1
b\tiny 1
b1间加电源
V
B
B
V\tiny BB
VBB,且发射极开路时,A点电位为
U
A
=
r
b
1
r
b
1
+
r
b
2
∗
V
B
B
=
η
V
B
B
{U\tiny A}=\frac {{\large r}{\tiny b1}}{{\large r}{\tiny b1}+{\large r}{\tiny b2}}*{V\tiny BB}={\eta}{V\tiny BB}
UA=rb1+rb2rb1∗VBB=ηVBB
式中
η
\eta
η称为单结晶管的分压比,其数值主要与管子的结构有关,一般在0.5 ~ 0.9之间。基极
b
2
b\tiny 2
b2的电流为
I
B
2
=
V
B
B
r
b
1
+
r
b
2
{I\tiny B2}=\frac {V\tiny BB}{{\large r}{\tiny b1}+{\large r}{\tiny b2}}
IB2=rb1+rb2VBB
当e -
b
1
b\tiny 1
b1间电压
u
E
B
1
{\large u}{\tiny EB1}
uEB1为零时,二极管承受反向电压,其值
u
E
A
=
−
η
V
B
B
{\large u}{\tiny EA}={-\eta V\tiny BB}
uEA=−ηVBB。发射极的电流
i
E
i\tiny E
iE为二极管的反向电流,记作
I
E
O
I\tiny EO
IEO。若缓慢增大
u
E
B
1
{\large u}{\tiny EB1}
uEB1,则二极管端电压
u
E
A
{\large u}{\tiny EA}
uEA随之增大;根据PN结的反向特性可知,只有当
u
E
A
{\large u}{\tiny EA}
uEA接近零时,
i
E
=
0
{i\tiny E}=0
iE=0。若
u
E
B
1
{\large u}{\tiny EB1}
uEB1继续增大,使PN结正向电压大于开启电压时,则
i
E
{i\tiny E}
iE变为正向电流,从发射极e流向基极
b
1
b\tiny 1
b1。此时,空穴浓度很高的P区向电子浓度很低的硅棒的A -
b
1
b\tiny 1
b1区注入的非平衡少子;由于半导体材料的电阻与其载流子的浓度紧密相关,注入的载流子使
r
b
1
r\tiny b1
rb1减小;而且
r
b
1
r\tiny b1
rb1的减小,使其压降减小,导致PN结正向电压增大,
i
E
i\tiny E
iE必然随之增大,注入的载流子将更多,于是
r
b
1
r\tiny b1
rb1进一步减小;当
i
E
i\tiny E
iE增大到一定程度时,二极管的导通电压将变化不大,此时
u
E
B
1
{\large u}{\tiny EB1}
uEB1将因
r
b
1
r\tiny b1
rb1的减小而减小,表现出负电阻特性。
所谓负电阻特性,是指输入电压(即
u
E
B
1
{\large u}{\tiny EB1}
uEB1)增大到某一数值后,输入电流(即发射极电流
i
E
i\tiny E
iE)越大,输入端的等效电阻越小的特性。
一旦单结晶体管进入负阻工作区域,输入电流的
i
E
i\tiny E
iE的增加只受输入回路外部电阻的限制,除非将输入回路开路或将
i
E
i\tiny E
iE减小到很小的数值,否则管子将始终保持导通状态。
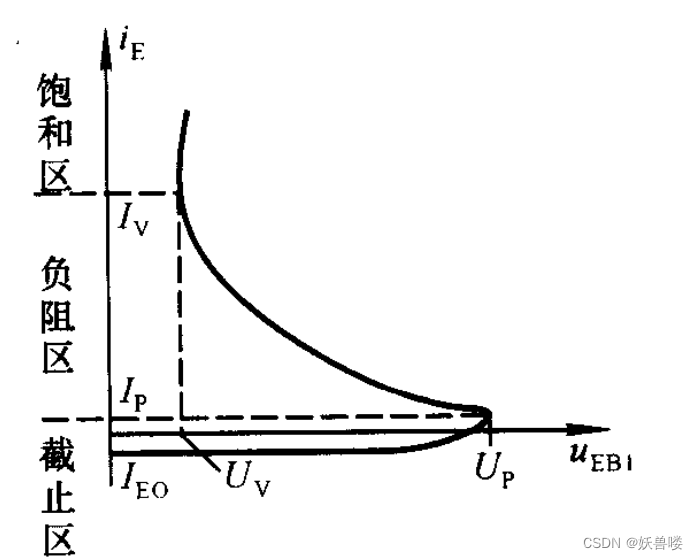
单结晶晶体管的特性曲线图如下图所示。当
u
E
B
1
=
0
{\large u}{\tiny EB1}=0
uEB1=0时,
i
E
=
I
E
O
{i\tiny E}=I{\tiny EO}
iE=IEO;当
u
E
B
1
{\large u}{\tiny EB1}
uEB1增大到
U
P
U\tiny P
UP(峰点电压)时,PN结开始正向导通,
U
P
=
u
A
+
U
o
n
{U\tiny P}={u\tiny A}+{U\tiny on}
UP=uA+Uon,
u
A
{u\tiny A}
uA如下式所示,
U
A
=
r
b
1
r
b
1
+
r
b
2
∗
V
B
B
=
η
V
B
B
{U\tiny A}=\frac {{\large r}{\tiny b1}}{{\large r}{\tiny b1}+{\large r}{\tiny b2}}*{V\tiny BB}={\eta}{V\tiny BB}
UA=rb1+rb2rb1∗VBB=ηVBB
U
o
n
{U\tiny on}
Uon为PN结的开启电压,此时
i
E
=
I
P
{i\tiny E}={I\tiny P}
iE=IP(峰点电流);
u
E
B
1
{\large u}{\tiny EB1}
uEB1再增大一点,管子就进入负阻区,随着
i
E
i\tiny E
iE增大,
r
b
1
r\tiny b1
rb1减小,
u
E
B
1
{\large u}{\tiny EB1}
uEB1减小,直至
u
E
B
1
=
U
V
{\large u}{\tiny EB1}={U\tiny V}
uEB1=UV(谷点电压),
i
E
=
I
V
{i\tiny E}=I{\tiny V}
iE=IV(谷点电流),
U
V
U{\tiny V}
UV取决于PN结的导通电压和
r
b
1
r\tiny b1
rb1的饱和电阻
r
S
r\tiny S
rS;当
i
E
i\tiny E
iE再增大,管子进入饱和区。单结晶体管的三个工作区域如下图所示。
单结晶体管的负阻特性广泛应用与定时电路和振荡电路中。除了单结晶体管外,具有负阻特性的器件还有隧道二极管、
λ
\lambda
λ双极性晶体管、负阻场效应管等等。
应用举例
下图所示为单结晶体管组成的振荡电路。所谓振荡,是指在没有输入信号的情况下,电路输出一定频率、一定幅值的电压或电流信号。

上图所示电路中,当合闸通电时,电容C上的电压为零,管子截止,电源
V
B
B
V\tiny BB
VBB通过电阻R对C充电,随时间增长电容上电压
u
C
u \tiny C
uC(即
u
E
B
1
{\large u}{\tiny EB1}
uEB1)逐渐增大,一旦
u
E
B
1
{\large u}{\tiny EB1}
uEB1增大到峰点电压
U
P
{U}{\tiny P}
UP后,管子进入负阻区,输入端等效电阻急剧减小,使C通过管子的输入回路迅速放电,
i
E
{i}{\tiny E}
iE随之迅速减小,一旦
u
E
B
1
{\large u}{\tiny EB1}
uEB1减小到谷点电压
U
V
{U}{\tiny V}
UV后,管子截止;电容又开始充电。上述过程循环往返,只有当断电时才会停止,因而产生振荡。由于充电时间常数远大于放电时间常数,当稳定振荡时,电容上电压的波形如下图所示。