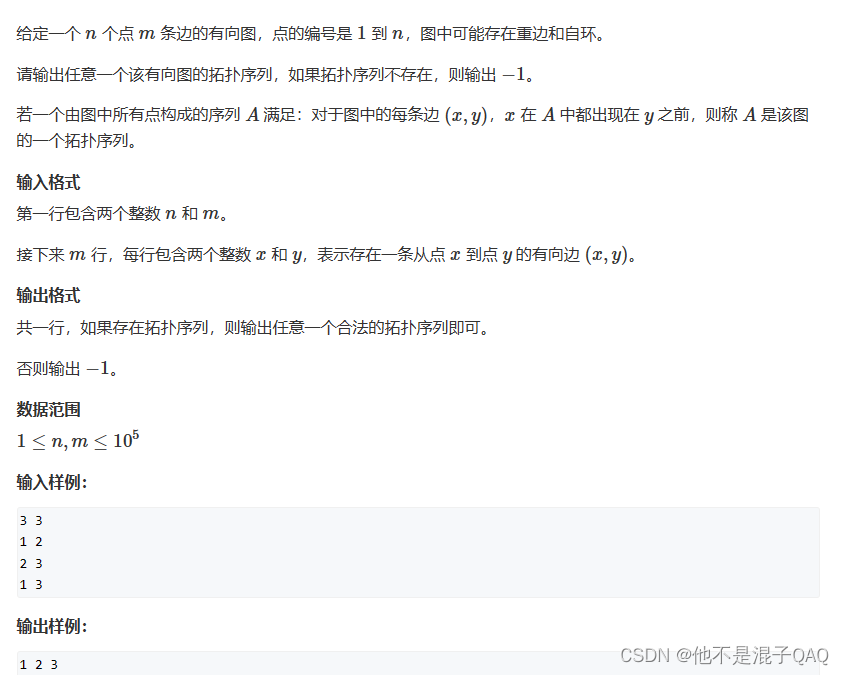
848. 有向图的拓扑序列 - AcWing题库

 昨天看了这道题L3-031 千手观音 拓扑排序+哈希表_他不是混子QAQ的博客-CSDN博客

就想着也用这道题的stl方法来试下

先来我的这个笨笨的方法，就当练习stl了，后面还有一个简便的stl

STL知识点(刚知道：

对于vector中是否有tmp这个元素 : count(v.begin(),v.end(),tmp)  

而对于map : m.count(tmp) 

还有一个就是 for (auto &[k,v] : d) 的使用 （见方法1）

 拓扑排序：

记录入度，先将入度为0的点放入队列，将队列的点依次出列，找出这个点发出的边，删除边，更新点的入度，再将入度为零的点入队，依次循环，直到队列空。如果存在拓扑排序，则存入了n个点，少于n个则不存在拓扑排序。

用队列来实现，如果要字典序输出的话，那么就优先队列实现

#include<bits/stdc++.h>
#include<unordered_map>
using namespace std;
int n, m;

unordered_map<string, vector<string>> g;//邻接表
unordered_map<string, int>d;//入度
queue<string> q;
int main()
{
	cin >> n >> m;
	while (m--)
	{
		string a, b;
		cin >> a >> b;
		if (!count(g[a].begin(), g[a].end(), b))//防止重复的边增加入度
		{
			g[a].push_back(b);
			d[b]++;
		}
		if (!d.count(a)) d[a] = 0;
        //这行很有必要，因为是map<string,string> 无这行d[a]就存不了
	}

	vector<string> res;
	for (auto &[k,v] : d)//先找到入度为0的点，存入队列中去
		if (v == 0) q.push(k);
	while (q.size())
	{
		string s = q.front();
		res.push_back(s);
		q.pop();
		for (auto& u : g[s])
			if (--d[u] == 0)
				q.push(u);

	}
	if (res.size() < n)
	{
		cout << -1 << endl;
		return 0;
	}
	else
	{
		for (auto x : res)
			cout << x << " ";
	}

	system("pause");
}

 因为这题给的是int类型的，直接用vector<int>g[N]存邻接表就好了

下面的这个就显得很简洁了，但是上面的代码可以来存字符串的情况（毕竟是千手观音那道题过来的）。

#include<bits/stdc++.h>
using namespace std;
const int N = 100010;
int n, m;
vector<int> g[N];
int d[N];
queue<int> q;
int main()
{
	cin >> n >> m;
	while (m--)
	{
		int a, b;
		cin >> a >> b;
		g[a].push_back(b);
		d[b]++;//显现出和map的区别了，这里全局变量自动为0，而map得判断下
	}
	for (int i = 1;i <= n;i++)
		if (!d[i]) q.push(i);
	
	vector<int> res;

	while (q.size())
	{
		int u = q.front();
		q.pop();
		res.push_back(u);
		for (auto x : g[u])
			if (--d[x] == 0) 
				q.push(x);
	}
	if(res.size()<n)
	{
		cout <<-1<< endl;
		return 0;
	}
	for (auto x : res) 
		cout << x << " ";
	
}

数组模拟队列的代码：

#include<bits/stdc++.h>
using namespace std;
const int N = 100010;
int n, m;
int h[N], e[N], ne[N], idx;
int q[N],d[N];

void add(int a, int b)
{
	e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

bool topsort()
{
	int hh = 0, tt = -1;

	for (int i = 1;i <= n;i++)
		if (!d[i]) q[++tt] = i;

	while (hh <= tt)
	{
		int t = q[hh++];
		for (int i = h[t];i != -1;i = ne[i])
		{
			int j = e[i];
			if (--d[j] == 0)
				q[++tt] = j;
		}
	}
	return tt == n - 1;
}
int main()
{
	cin >> n >> m;
	memset(h, -1, sizeof h);
	while (m--)
	{
		int a, b;
		cin >> a >> b;
		add(a, b);
		d[b]++;
	}
	if (!topsort()) cout << -1;
	else
		for (int i = 0;i < n;i++) cout << q[i] << " ";
}