KMP算法核心剖析：

关于KMP算法，建议先了解 BF算法

KMP算法是用来解决字符串匹配问题的高级算法，看完这篇文章，你应该能理解KMP算法。

KMP算法和BF算法唯一的区别在于：主串的ｉ　并不会回退，子串的ｊ也不会回退到０位置。

KMP算法的核心在于求出子串的next数组

所谓的next数组，其实存放的就是子串回退的位置的下标。

下面来演示如何求出一个子串的next 数组
假设有一个字符串：“ababcabcdab”, 求该字符串的next数组：

规定：next[0] = -1 , next[1] = 0

下面就来求next[2] ，next[3]…

如上图：
那么next[2]如何求呢？

来看下面：
规则：

1、规则:找到匹配成功部分的两个相等的真子串(不包含本身)，一个以下标0字符开始，另一个以j - 1下标字符结尾。
2、不管什么数据next[0] =-1;next[1]= 0;在这里，我们以下标来开始，而说到的第几个第几个是从1开始;

第二点已经说过，那么第一点是什么意思呢？
看下面：
对于p数组：该数组存有上面举例的字符串： ababcabcdab ,
p[2] = a， 求这个位置的next 值，根据规则1，找到匹配成功部分的两个相等的真子串，一个下标0 字符开始， 另一个是j-1 结尾

意思就是一个串从下标0开始，另一个串从下标1结尾，对于p[2] , p[0] = a, p[2-1] = b，没有两个相等的真子串，即长度为0 ，故next[2] = 0。

看不懂没关系，继续看下面：
求next[3]：，p[0] = a,p[3-1] = a，所以该子串是以a开始，另一个串以a结尾，所以只有a 和 a 这两个串匹配，长度为1 ，故next[3] = 1;

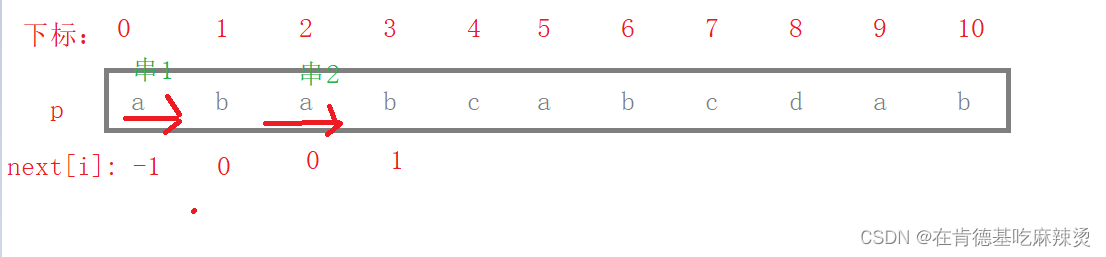
求next[4]：，p[0]= a,p[4-1] = b，该两串以a开始，以b结尾，故有两个串是ab和ab匹配，长度为2，所以next[4] = 2;

求next[5]：，p[0] = a,p[5-1] = c,该两串一个以a开始，一个以c结尾，找不出相等的两子串，故长度为0，所以next[5] = 0.

求next[6]：，p[0]= a,p[6-1] = a，该两串以a开始，另一个以a结尾，然而串1往后走，走到以a结尾是 aba， 串2往回走，走到以a开始是
abca ，两者不同，故长度只有a 和 a 两个串，长度为1，即next[6] = 1

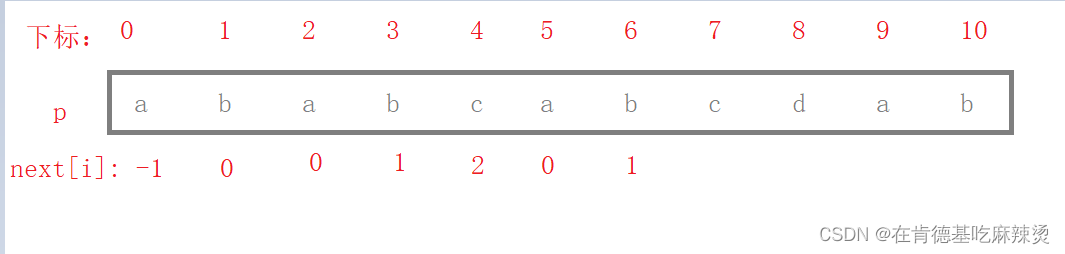
求next[7]：，p[0] = a,p[7-1] = b，该串以a开始，以b结尾，有这样的长度的，只有串1 为ab，串2 为ab ，如下图：

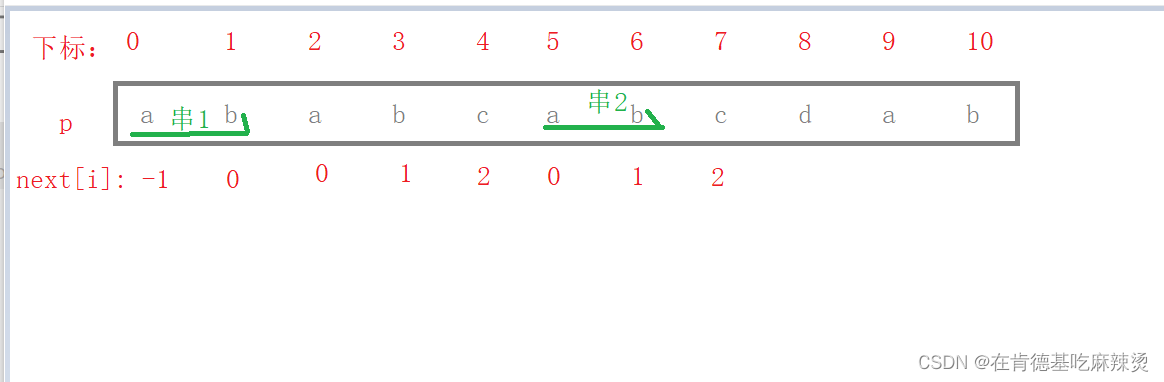
求next[8]，p[0] = a，p[8-1] = c ，由于c是新增的，故长度为0，没有相同的两串是以a开始，另一个以c结尾。next[8] = 0

求next[9]: p[0] = a , p[9-1] = d ，由于d也是新增的，没有相同的两串是一个以a开始，一个以d结尾，故长度为0 .
求next[10] ,p[0] = a,p[10-1] = a，一串以a开始，一串以a结尾，故只有这两个串a和a，故长度为1. next[10] = 1.

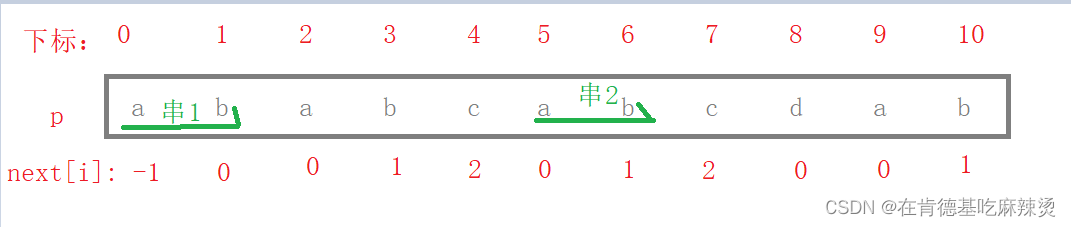
求完next数组后， KMP算法核心就结束了。

有一条规律：next[i]往后走的时候，后一个数如果比前一个数大，那一定是大一位 ， 如果比前一个数小，可能小1，2，…
重点是后一个数如果比前一个数大，那一定是大一位
由此我们可以得到另一条结论：

先看上图：假设i 和 k 的位置如上图：（k是如果在i的位置与主串不匹配，那么子串回退到的位置：就是k下标的位置。）
我们求next数组的时候，是肉眼来求的，但是当我们写代码的时候，next数组是一个个往后求的，所以这里，就是已知 i ，求 i+1的next数组，
情况1>>如果p[i] == p[k]，那么next[i+1] = k+1，(注意：i和k都是下标)
所以next[i+1] = 1+1 = 2。

情况2>> 如果p[i] !=p[k] , 那么k就不是我们要找的， 所以k需要继续回退，k回退到他所在的next[k] 位置，即 k = next[k]，next[k] = 0,
所以k继续回退到0位置，此时 p[i] == p[k] ,所以next[i+1] = k+1 = 0+1 = 1.

情况2其实就是继续回退，找到情况1。

上面这两条结论，就是我们要写代码时 要用到的结论，
但是我们正常来求next数组，是用肉眼来求的，不需要这些结论。

总结：

写代码求next数组时用到的两条结论：

情况1>>如果p[i] == p[k]，那么next[i+1] = k+1，(注意：i和k都是下标)
所以next[i+1] = 1+1 = 2。

情况2>> 如果p[i] !=p[k] , 那么k就不是我们要找的， 所以k需要继续回退，k回退到他所在的next[k] 位置，即 k = next[k]

下面就可以开始写代码了，

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<assert.h>

void GetNext(const char* sub, int*next,int len_sub)
{
	assert(sub);
	next[0] = -1;
	next[1] = 0;
	int j = 2;//j是下标->下标从0开始
	int k = 0;//k是下标
	while (j < len_sub)//所以这里没有等号
	{
		if (k==-1 || sub[j-1] == sub[k]) // 情况1
		{ // k==-1也就是极端情况，一开始匹配就不相等，既然不相等，长度就为0，next对应的长度就为0
			next[j] = k + 1;
			j++;
			k++;
		}
		else //情况2
		{
			k = next[k];
		}
	}
}

先来趁热打铁，求next数组。

看不懂代码先不急，看看上图，
我们求的是j 所对应的next数组的值，现在知道了 j-1 了，故从j-1开始比较，（也因为j 是下标，下标从0开始 ）

会求next数组，也就成功了%60

int KMP(const char* str, const char* sub , int pos)
{
	assert(str && sub);
	int len_str = strlen(str);
	int len_sub = strlen(sub);
	if (len_str == 0)
	{
		return -1;//主串长度为0,找不到
	}
	if (len_sub == 0)
	{
		return 0;//子串长度为0，返回主串起始位置
	}
	if (pos<0 || pos>=len_sub)
	{
		return -1;//参数不在主串长度的有效范围内
	}
	int* next = (int*)malloc(sizeof(int) * len_sub);
	GetNext(sub,next,len_sub);
	//求子串的next数组

	int i = pos;//记录主串位置
	int j = 0;//记录子串位置

	while (i < len_str && j< len_sub)
	{
		if (j==-1 || str[i] == sub[j])
		{//j==-1是极端情况，即一开始匹配就不相等，
			i++;
			j++;
		}
		else
		{
			j = next[j];//j回退到next[j]的位置
		}
	}
	if (j >= len_sub)
	{
		return i - j;//子串找完了，找到了
	}
	return -1;//退出循环只有两者情况，不是上面那种，就是找完主串都找不到
}


int main()
{
	printf("%d\n", KMP("abbbcdef", "bbc", 0));
	return 0;
}

这是剩下的%40，情况与BF算法类似，你可以尝试着运行，看看结果正确与否。