什么是归并排序:
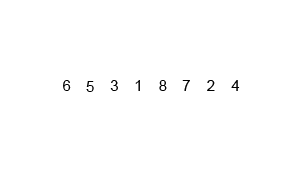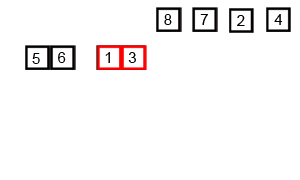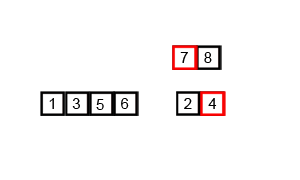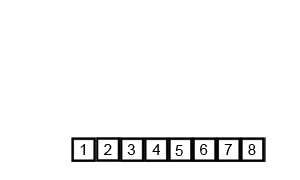
归并排序是一种基于分治法的排序算法。它的基本思想是将待排序的序列分成若干个子序列,分别进行排序,然后再将已排序的子序列合并成一个有序的序列。
基本思想:
归并排序是用分治思想,分治模式在每一层递归上有三个步骤:
- 分解(Divide):将n个元素分成个含n/2个元素的子序列。
- 解决(Conquer):用合并排序法对两个子序列递归的排序。
- 合并(Combine):合并两个已排序的子序列已得到排序结果。
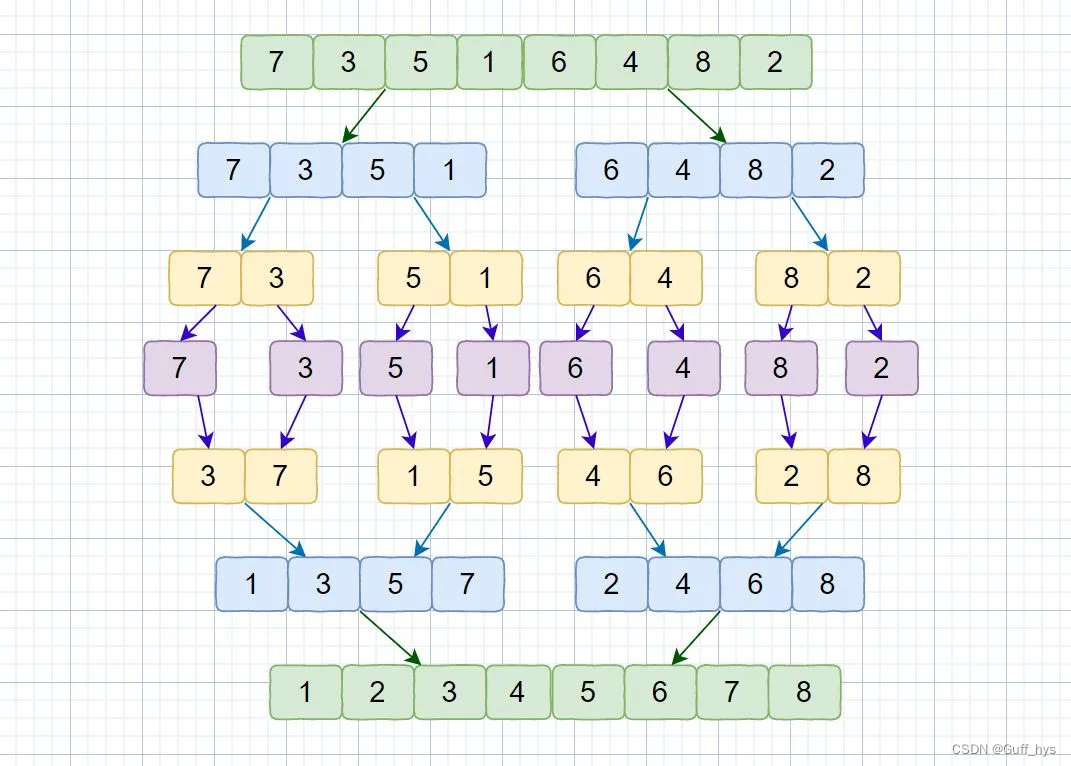
具体来说,归并排序的过程如下:
1. 将待排序的序列不断地二分,直到每个子序列只包含一个元素。
2. 将相邻的子序列两两合并,合并过程中按照大小顺序将元素逐个放入临时数组中。
3. 不断重复上述步骤,直到所有子序列合并成一个有序的序列。
归并排序的时间复杂度为O(nlogn),它是一种稳定的排序算法,适合对大规模数据进行排序。
归并排序的优点包括:
1. 时间复杂度稳定:归并排序的时间复杂度为O(nlogn),在大多数情况下都能保持这个性能。
2. 稳定性:归并排序是一种稳定的排序算法,相同元素的相对位置不会改变。
3. 适合大规模数据:归并排序适合对大规模数据进行排序,因为它的时间复杂度不会随着数据规模的增加而大幅度增加。
缺点包括:
1. 需要额外空间:归并排序需要额外的空间来存储临时数组,因此空间复杂度较高。
2. 不适合小规模数据:在数据规模较小的情况下,归并排序的性能可能不如其他排序算法,因为它需要不断地进行数组分割和合并操作。
3. 实现复杂:相对于其他简单的排序算法,归并排序的实现可能比较复杂,需要理解递归和合并的过程。
代码:
def merge_sort(alist):
n=len(alist)
if n <= 1:
return alist
mid=n//2
left_li = merge_sort(alist[:mid])
right_li = merge_sort(alist[mid:])
left_pointer,right_pointer=0,0
result=[]
while left_pointer<len(left_li) and right_pointer<len(right_li):
if left_li[left_pointer] <= right_li[right_pointer]:
result.append(left_li[left_pointer])
left_pointer += 1
else:
result.append(right_li[right_pointer])
right_pointer+=1
result += left_li[left_pointer:]
result += right_li[right_pointer:]
return result
if __name__=="__main__":
print(merge_sort([214,1,234,3,57,43,23,234]))