数据结构-考研难点代码突破（C++实现无向图图最小生成树算法（Prim，Kruskal）图解操作细节（引自C语言中文网））

news2024/11/19 18:21:23

以代码的方式复习考研数据结构知识点，这里在考研不以代码为重点，而是以实现过程为重点

文章目录

  • 1. 无向图最小生成树算法
    • Kruskal算法
      • C++代码实现
    • Prim算法
      • C++代码实现

1. 无向图最小生成树算法

常见基本概念记忆：

生成树定义：
无向图中一个连通图的最小连通子图称为生成树。（用最少的边把所有顶点连接起来）。n个顶点的连通图的生成树有n-1条边。

路径长度：对于不带权图为路径的边个数。带权图为路径所有边权值的和

最小生成树：所有生成树中，路径长度最小的生成树。

所以生成树一定是连通图。这个定义是在无向图的基础上开展的。

连通图：无向图中，若顶点A、B存在路径，称为A、B连通。若图中的任意两点都是连通的，则称此图为连通图。

构造最小生成树的方法：Kruskal算法和Prim算法。这两个算法都采用了逐步求解的贪心策略。

最小生成树的性质

  1. 最小生成树不是唯一的，即最小生成树的树形不唯一，田中可能有多个最小生成树。

    当图G中的各边权值互不相等时，G的最小生成树是唯一的；

    若无向连通图G的边数比顶点数少1，即G本身是一棵树时，则G的最小生成树就是它本身。

  2. 最小生成树的边的权值之和总是唯一的，虽然最小生成树不唯一，但其对应的边的权值之和总是唯一的，而且是最小的。

  3. 最小生成树的边数为顶点数减1。

Kruskal算法

克鲁斯卡尔算法查找最小生成树的方法是：将连通网中所有的边按照权值大小做升序排序，从权值最小的边开始选择，只要此边不和已选择的边一起构成环路，就可以选择它组成最小生成树。对于 N 个顶点的连通网，挑选出 N-1 条符合条件的边，这些边组成的生成树就是最小生成树。

Kruskal算法时间复杂度与图的边有关，与顶点无关，为O(ElogE)
Kruskal算法适合边稀疏而顶点较多的图

eg：C语言中文网
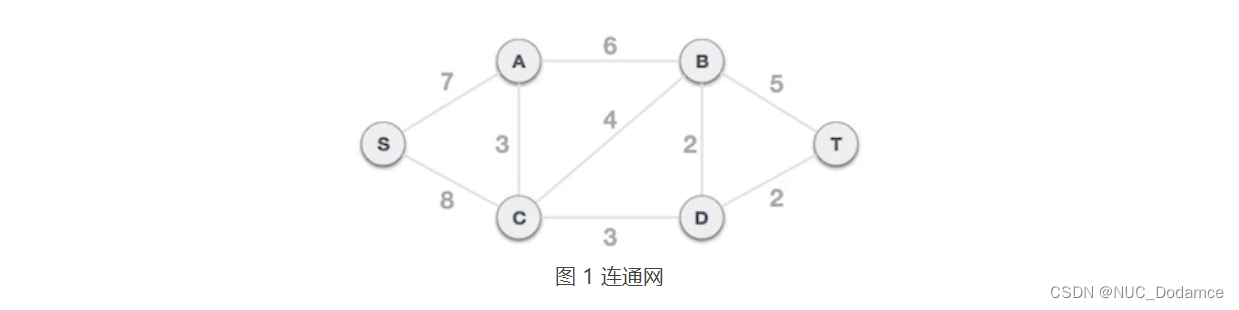
在这里插入图片描述

具体实现步骤：

  1. 将连通网中的所有边按照权值大小做升序排序

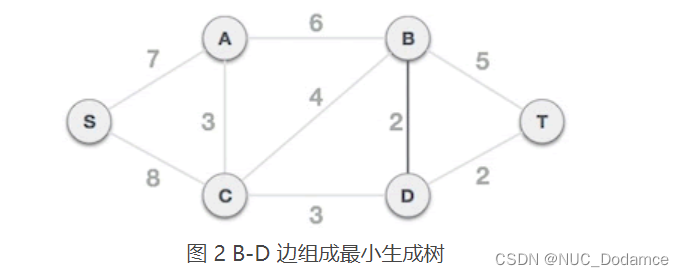
    在这里插入图片描述

  2. 从 B-D 边开始挑选，由于尚未选择任何边组成最小生成树，且 B-D 自身不会构成环路，所以 B-D 边可以组成最小生成树。

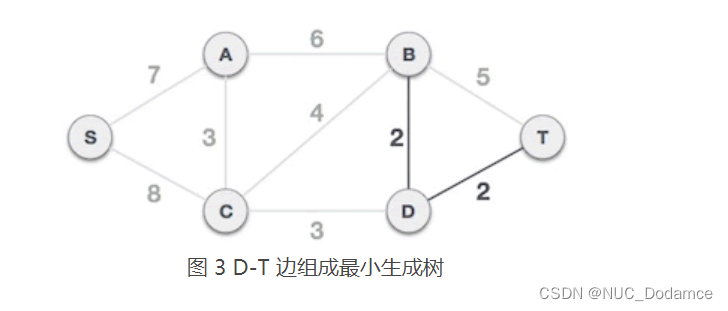
    在这里插入图片描述

  3. D-T 边不会和已选 B-D 边构成环路，可以组成最小生成树

    在这里插入图片描述

  4. A-C 边不会和已选 B-D、D-T 边构成环路，可以组成最小生成树
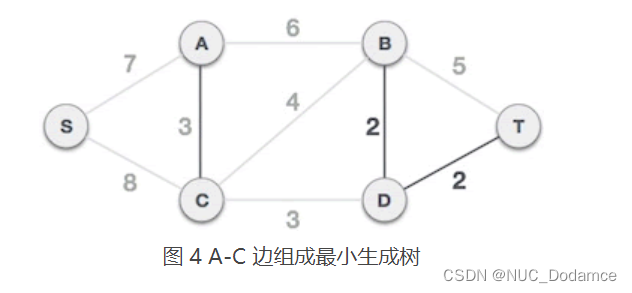
    在这里插入图片描述

  5. C-D 边不会和已选 A-C、B-D、D-T 边构成环路，可以组成最小生成树

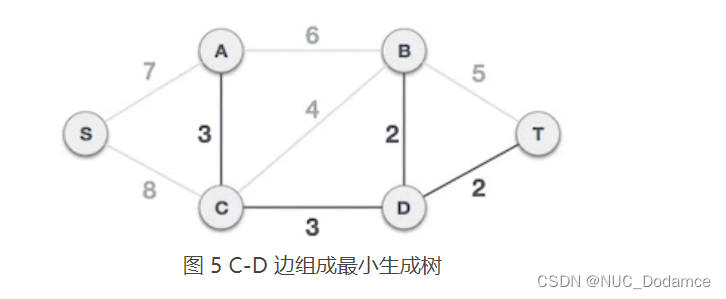
    在这里插入图片描述

  6. C-B 边会和已选 C-D、B-D 边构成环路，因此不能组成最小生成树

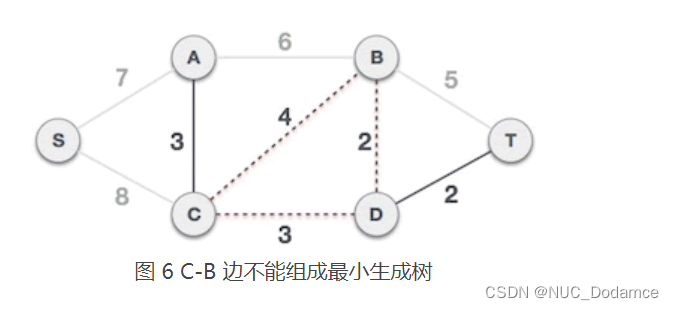
    在这里插入图片描述

  7. B-T 、A-B、S-A 三条边都会和已选 A-C、C-D、B-D、D-T 构成环路，都不能组成最小生成树。而 S-A 不会和已选边构成环路，可以组成最小生成树。

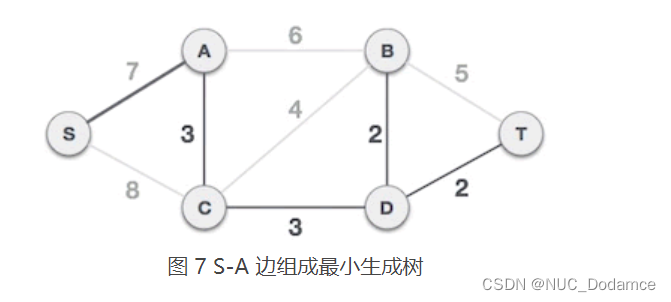
    在这里插入图片描述

综上所述构造的最小生成树为：
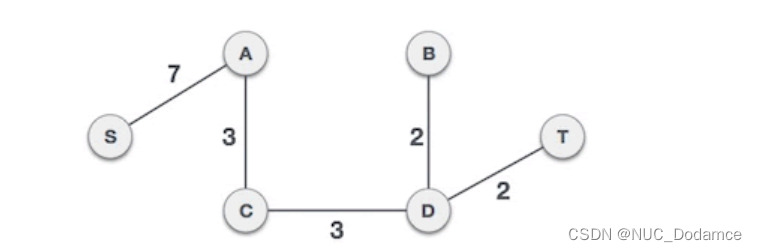
在这里插入图片描述

C++代码实现

  1. 权值从小到大排序使用C++优先级队列完成。默认大顶堆，我们这里要使用小顶堆
  2. 判断图是否产生闭环，可以采用并查集的方式。如果这个边的顶点在并查集中，则说明如果添加这条边的话就构成环

数据结构-难点突破（C++实现并查集+路径优化，详解哈夫曼编码树）

为了简单，这里的图全部采用邻接矩阵存储，算法整体难度不高

并查集代码：

// 构建并查集

#include <assert.h>
#include <vector>
#include <stdio.h>

class UnionFindSet
{
private:
    // 数组的下标保存的是并查集的数据，数组的值记录的是并查集这个节点的父节点下标
    std::vector<int> ufs;

public:
    UnionFindSet(size_t size)
    {
        ufs.resize(size, -1);
    }

    // x和y所在的两个集合合并
    void Union(int x, int y)
    {
        assert(x < ufs.size() && y < ufs.size());
        int root_x = FindRoot(x);
        int root_y = FindRoot(y);

        if (root_x != root_y)
        {
            // 不在一棵树上
            ufs[root_x] += ufs[root_y];
            ufs[root_y] = root_x;
        }
    }

    // 找data的根
    int FindRoot(int data)
    {
        int root = data;
        while (ufs[root] >= 0)
        {
            root = ufs[root];
        }

        // 找到根后，这里做优化，降低并查集树的高度
        // 把这个节点到根节点路径上的所有节点插入到根节点上
        while (data != root)
        {
            int parent = ufs[data];
            ufs[data] = root;
            data = parent;
        }
        return root;
    }

    // 获取并查集中树的个数
    int GetTreeSize()
    {
        int ret = 0;
        for (int i = 0; i < ufs.size(); i++)
        {
            if (ufs[i] < 0)
                ret += 1;
        }
        return ret;
    }

    // 打印并查集信息
    void PrintUfs()
    {
        for (int i = 0; i < ufs.size(); i++)
        {
            printf("%2d ", i);
        }
        printf("\n");
        for (int i = 0; i < ufs.size(); i++)
        {
            printf("%2d ", ufs[i]);
        }
        printf("\n");
    }

    //判断两个点是否在一个集合中
    bool IsSameSet(int left, int right) {
        return FindRoot(left) == FindRoot(right);
    }
};

无向图，邻接矩阵，Kruskal算法：

// 邻接矩阵法存储图结构

#include <iostream>
#include <assert.h>
#include <map>
#include <vector>
#include <stdio.h>
#include <queue>

#include "UnionFindSet.h"

// v:图顶点保存的值。w:边的权值 max:最大权值，代表无穷。flag=true代表有向图。否则就是无向图
template <class v, class w, w max = INT_MAX, bool flag = false>
class graph
{
private:
    std::vector<v> _verPoint;            // 顶点集合
    std::map<v, int> _indexMap;          // 顶点与下标的映射
    std::vector<std::vector<w>> _matrix; // 邻接矩阵

    int _getPosPoint(const v &point)
    {
        if (_indexMap.find(point) != _indexMap.end())
        {
            return _indexMap[point];
        }
        else
        {
            std::cout << point << " not found" << std::endl;
            return -1;
        }
    }

public:
    graph() = default;
    // 根据数组来开辟邻接矩阵
    graph(const std::vector<v> &src)
    {
        _verPoint.resize(src.size());
        for (int i = 0; i < src.size(); i++)
        {
            _verPoint[i] = src[i];
            _indexMap[src[i]] = i;
        }

        // 初始化邻接矩阵
        _matrix.resize(src.size());
        for (int i = 0; i < src.size(); i++)
        {
            _matrix[i].resize(src.size(), max);
        }
    }
    // 添加边的关系,输入两个点，以及这两个点连线边的权值。
    void AddEdge(const v &pointA, const v &pointB, const w &weight)
    {
        // 获取这个顶点在邻接矩阵中的下标
        int posA = _getPosPoint(pointA);
        int posB = _getPosPoint(pointB);
        _matrix[posA][posB] = weight;
        if (!flag)
        {
            // 无向图,邻接矩阵对称
            _matrix[posB][posA] = weight;
        }
    }

    // 打印邻接矩阵
    void PrintGraph()
    {
        // 打印顶点对应的坐标
        typename std::map<v, int>::iterator pos = _indexMap.begin();
        while (pos != _indexMap.end())
        {
            std::cout << pos->first << ":" << pos->second << std::endl;
            pos++;
        }
        std::cout << std::endl;

        // 打印边
        printf("  ");
        for (int i = 0; i < _verPoint.size(); i++)
        {
            std::cout << _verPoint[i] << " ";
        }
        printf("\n");

        for (int i = 0; i < _matrix.size(); i++)
        {
            std::cout << _verPoint[i] << " ";
            for (int j = 0; j < _matrix[i].size(); j++)
            {
                if (_matrix[i][j] == max)
                {
                    // 这条边不通
                    printf("∞ ");
                }
                else
                {
                    std::cout << _matrix[i][j] << " ";
                }
            }
            printf("\n");
        }
        printf("\n");
    }
    // -------------------------------------Kruskal--------------------------------------------
    typedef graph<v, w, max, flag> self;

    // 代表图的一条边
    struct edge
    {
        size_t src;
        size_t dst;
        w weight;
        edge(size_t _src, size_t _dst, w _weight)
        {
            this->src = _src;
            this->dst = _dst;
            this->weight = _weight;
        }
    };

    // 小堆排序规则，从小到打排序
    struct rules
    {
        bool operator()(const edge &left, const edge &right)
        {
            return left.weight > right.weight;
        }
    };

    // 最小生成树，返回最小生成树权值，传入一个图，这个参数是输入输出参数，函数结束后，minTree是图的最小生成树
    w kruskal(self &minGraph)
    {
        size_t size = _verPoint.size();
        minGraph._verPoint = _verPoint;
        minGraph._indexMap = _indexMap;

        // 初始化最小生成树的邻接矩阵
        minGraph._matrix.resize(size);
        for (size_t i = 0; i < size; i++)
        {
            minGraph._matrix[i].resize(size, max);
        }

        std::priority_queue<edge, std::vector<edge>, rules> queue;

        // 将所有的边添加到优先级队列中,因为是无向图的边,所以只需要遍历一半数组即可
        for (size_t i = 0; i < size; i++)
        {
            for (size_t j = 0; j < i; j++)
            {
                if (_matrix[i][j] != max)
                {
                    queue.push(edge(i, j, _matrix[i][j]));
                }
            }
        }

        // 选出n-1条边
        int dstSize = 0;
        w total = w();
        // 创建并查集来标记是否成环,大小为图顶点个数。
        UnionFindSet unionSet(size);

        while (!queue.empty())
        {
            edge MinEdge = queue.top();
            queue.pop();
            // 判断这条边顶点是否在并查集中，在并查集中构成环，不符合最小生成树定义。
            if (!unionSet.IsSameSet(MinEdge.src, MinEdge.dst))
            {
                // 打印选的边测试
                //std::cout << _verPoint[MinEdge.src] << "->" << _verPoint[MinEdge.dst] << " 权值：" << MinEdge.weight << "\n";

                minGraph.AddEdge(_verPoint[MinEdge.src], _verPoint[MinEdge.dst], MinEdge.weight);
                unionSet.Union(MinEdge.src, MinEdge.dst);

                dstSize += 1;
                total += MinEdge.weight;
            }
        }

        if (dstSize != size - 1)
        {
            // 没有找到生成树
            std::cout << "没有找到生成树" << std::endl;
            return w();
        }
        return total;
    }
};

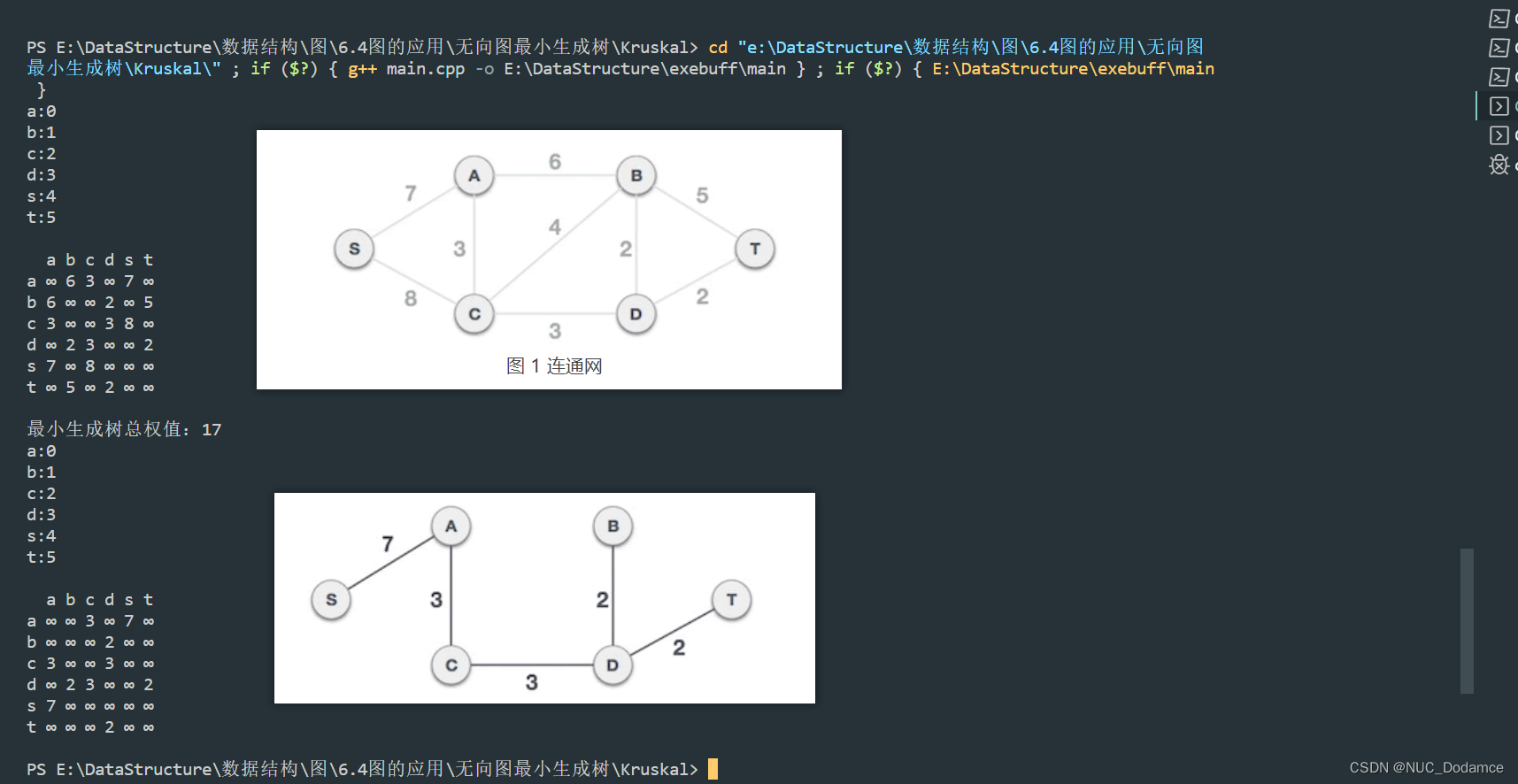
测试代码与结果图

#include "matrix.h"

using namespace std;

int main(int argc, char const *argv[])
{
    vector<char> vet = {'a', 'b', 'c', 'd', 's', 't'};
    graph<char, int> Graph(vet);
    Graph.AddEdge('a', 'b', 6);
    Graph.AddEdge('b', 't', 5);
    Graph.AddEdge('t', 'd', 2);
    Graph.AddEdge('d', 'c', 3);
    Graph.AddEdge('c', 's', 8);
    Graph.AddEdge('s', 'a', 7);
    Graph.AddEdge('c', 'a', 3);
    Graph.AddEdge('c', 's', 8);
    Graph.AddEdge('b', 'd', 2);
    Graph.PrintGraph();

    graph<char, int> minGraph;
    cout << "最小生成树总权值：" << Graph.kruskal(minGraph) << endl;
    minGraph.PrintGraph();
    return 0;
}

在这里插入图片描述

Prim算法

与Kruskal算法类似，Prim算法也是通用最小生成树算法的一个特例。
Prim算法的工作原理与Dijkstra最短路径算法类似，也是使用局部贪心。

Prim算法：
开始指出一个起点，从起点开始找最小生成树。Prim算法将所有顶点分成两部分：已经选入的点，未选入的点。算法思路是从未选入部分顶点中选出一个点，再从选入的点中选择一个。这两个点的关系是：直接相连构成边，且这条边是所有选择中权值最小的。将选则的点添加到已经选择部分顶点集合中。

Prim算法的时间复杂度为 O(N2)，不依赖于边，依赖顶点个数，因此它适用于求解边稠密的图的最小生成树

具体实现步骤：
eg：C语言中文网
在这里插入图片描述

  1. 将图中的所有顶点分为 A 类和 B 类，初始状态下，A = {}，B = {A, B, C, D, S, T}。
  2. 从 B 类中任选一个顶点，假设选择 S 顶点，将其从 B 类移到 A 类，A = {S}，B = {A, B, C, D, T}。从 A 类的 S 顶点出发，到达 B 类中顶点的边有 2 个，分别是 S-A 和 S-C，其中 S-A 边的权值最小，所以选择 S-A 边组成最小生成树，将 A 顶点从 B 类移到 A 类，A = {S, A}，B = {B, C, D, T}。

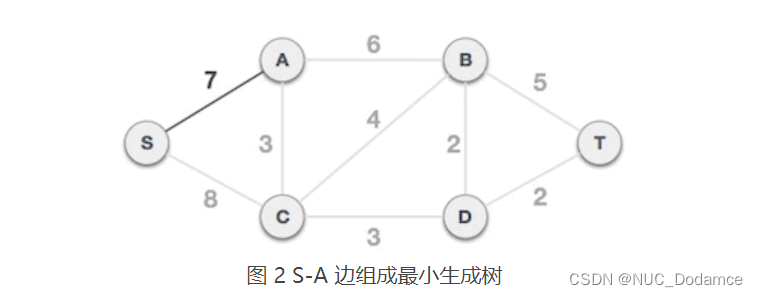
在这里插入图片描述

  1. 从 A 类中的 S、A 顶点出发，到达 B 类中顶点的边有 3 个，分别是 S-C、A-C、A-B，其中 A-C 的权值最小，所以选择 A-C 组成最小生成树，将顶点 C 从 B 类移到 A 类，A = {S, A, C}，B = {B, D, T}。
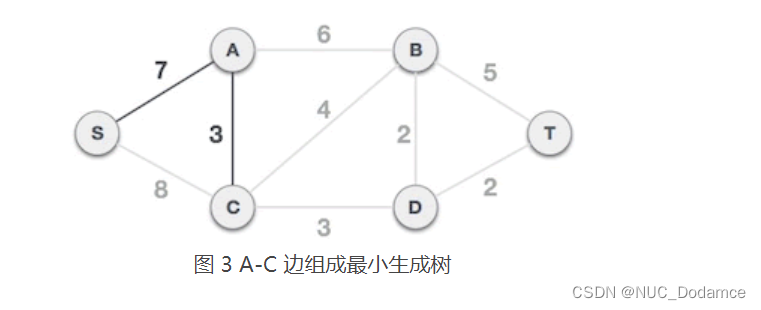
    在这里插入图片描述
  2. 从 A 类中的 S、A、C 顶点出发，到达 B 类顶点的边有 S-C、A-B、C-B、C-D，其中 C-D 边的权值最小，所以选择 C-D 组成最小生成树，将顶点 D 从 B 类移到 A 类，A = {S, A, C, D}，B = {B, T}。
    在这里插入图片描述
  3. 从 A 类中的 S、A、C、D 顶点出发，到达 B 类顶点的边有 A-B、C-B、D-B、D-T，其中 D-B 和 D-T 的权值最小，任选其中的一个，例如选择 D-B 组成最小生成树，将顶点 B 从 B 类移到 A 类，A = {S, A, C, D, B}，B = {T}。
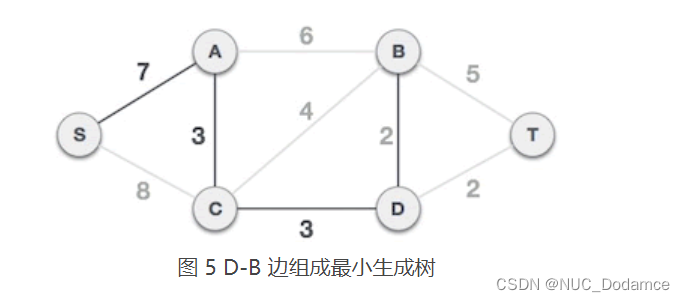
    在这里插入图片描述
  4. 从 A 类中的 S、A、C、D、B 顶点出发，到达 B 类顶点的边有 B-T、D-T，其中 D-T 的权值最小，选择 D-T 组成最小生成树，将顶点 T 从 B 类移到 A 类，A = {S, A, C, D, B, T}，B = {}。

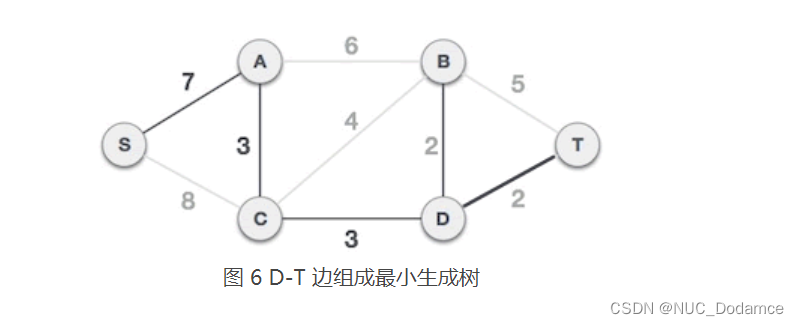
在这里插入图片描述
综上，使用Prim算法可以得出最小生成树为：
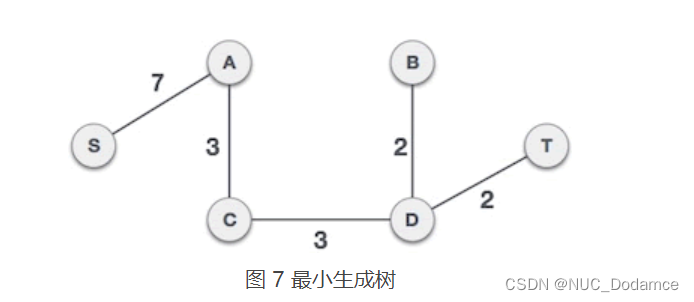
在这里插入图片描述

C++代码实现

通过上面的流程图分析可知，这个算法不需要并查集来判断是否成环。

但是这里处理时使用优先级队列，因为优先级队列开始时把顶点周围的所有边添加进去，而优先级队列又不支持指定删除元素。所以当优先级队列弹出最小权值边的时候，还需要判断这条边的两个顶点是不是在同一个数组，如果在同一个数组，说明这条边构成环。

在书写代码时，只要记得不要构成环即可，剩下步骤按照流程图走即可

无向图，邻接矩阵，Prim算法

// 邻接矩阵法存储图结构

#include <iostream>
#include <assert.h>
#include <map>
#include <vector>
#include <stdio.h>
#include <queue>

// v:图顶点保存的值。w:边的权值 max:最大权值，代表无穷。flag=true代表有向图。否则就是无向图
template <class v, class w, w max = INT_MAX, bool flag = false>
class graph
{
private:
    std::vector<v> _verPoint;            // 顶点集合
    std::map<v, int> _indexMap;          // 顶点与下标的映射
    std::vector<std::vector<w>> _matrix; // 邻接矩阵

    int _getPosPoint(const v &point)
    {
        if (_indexMap.find(point) != _indexMap.end())
        {
            return _indexMap[point];
        }
        else
        {
            std::cout << point << " not found" << std::endl;
            return -1;
        }
    }

public:
    graph() = default;
    // 根据数组来开辟邻接矩阵
    graph(const std::vector<v> &src)
    {
        _verPoint.resize(src.size());
        for (int i = 0; i < src.size(); i++)
        {
            _verPoint[i] = src[i];
            _indexMap[src[i]] = i;
        }

        // 初始化邻接矩阵
        _matrix.resize(src.size());
        for (int i = 0; i < src.size(); i++)
        {
            _matrix[i].resize(src.size(), max);
        }
    }
    // 添加边的关系,输入两个点，以及这两个点连线边的权值。
    void AddEdge(const v &pointA, const v &pointB, const w &weight)
    {
        // 获取这个顶点在邻接矩阵中的下标
        int posA = _getPosPoint(pointA);
        int posB = _getPosPoint(pointB);
        _matrix[posA][posB] = weight;
        if (!flag)
        {
            // 无向图,邻接矩阵对称
            _matrix[posB][posA] = weight;
        }
    }

    // 打印邻接矩阵
    void PrintGraph()
    {
        // 打印顶点对应的坐标
        typename std::map<v, int>::iterator pos = _indexMap.begin();
        while (pos != _indexMap.end())
        {
            std::cout << pos->first << ":" << pos->second << std::endl;
            pos++;
        }
        std::cout << std::endl;

        // 打印边
        printf("  ");
        for (int i = 0; i < _verPoint.size(); i++)
        {
            std::cout << _verPoint[i] << " ";
        }
        printf("\n");

        for (int i = 0; i < _matrix.size(); i++)
        {
            std::cout << _verPoint[i] << " ";
            for (int j = 0; j < _matrix[i].size(); j++)
            {
                if (_matrix[i][j] == max)
                {
                    // 这条边不通
                    printf("∞ ");
                }
                else
                {
                    std::cout << _matrix[i][j] << " ";
                }
            }
            printf("\n");
        }
        printf("\n");
    }
    // -------------------------------------Prim--------------------------------------------
    typedef graph<v, w, max, flag> self;

    // 代表图的一条边
    struct edge
    {
        size_t src;
        size_t dst;
        w weight;
        edge(size_t _src, size_t _dst, w _weight)
        {
            this->src = _src;
            this->dst = _dst;
            this->weight = _weight;
        }
    };

    // 小堆排序规则，从小到打排序
    struct rules
    {
        bool operator()(const edge &left, const edge &right)
        {
            return left.weight > right.weight;
        }
    };

    // 最小生成树，返回最小生成树权值，传入一个图，这个参数是输入输出参数，函数结束后，minTree是图的最小生成树
    // src:Prim算法传入的起始点
    w Prim(self &minGraph, const v &src)
    {
        size_t pos = _getPosPoint(src);

        // 初始化minTree
        minGraph._verPoint = _verPoint;
        minGraph._indexMap = _indexMap;
        size_t size = _verPoint.size();
        minGraph._matrix.resize(size);
        for (size_t i = 0; i < size; i++)
        {
            minGraph._matrix[i].resize(size, max);
        }

        std::vector<bool> A(size, false); // 已经加入的顶点的集合
        std::vector<bool> B(size, true);  // 未加入的顶点的集合
        A[pos] = true;
        B[pos] = false;

        // 从两个集合中选择两个点，构成权值最小的边
        std::priority_queue<edge, std::vector<edge>, rules> queue;
        // 将这个点连接的周围的点入队列
        for (int i = 0; i < size; i++)
        {
            if (_matrix[pos][i] != max)
            {
                queue.push(edge(pos, i, _matrix[pos][i]));
            }
        }

        // 选择权值最小的边
        size_t dstSize = 0;
        w total = w();

        while (!queue.empty())
        {
            edge minEdge = queue.top();
            queue.pop();

            // 如果这条边的两个点都在同一个集合中，那么说明构成环
            if (A[minEdge.dst])
            {
                // 构成环
                continue;
            }

            // DEBUG:
            //std::cout << minEdge.src << "->" << minEdge.dst << " 权值：" << minEdge.weight << "\n";

            minGraph.AddEdge(_verPoint[minEdge.src], _verPoint[minEdge.dst], minEdge.weight);

            A[minEdge.dst] = true;
            B[minEdge.dst] = false;

            dstSize += 1;
            total += minEdge.weight;
            if (dstSize == size - 1)
            {
                // size个点选了size-1条边，已经结束了
                break;
            }
            // 将minEdge.dst这个点周围的边(除了minEdge.dst->minEdge.src这条边)入队列，同时保证不构成环
            for (size_t i = 0; i < size; i++)
            {
                if (_matrix[minEdge.dst][i] != max && A[i] == false)
                {
                    queue.push(edge(minEdge.dst, i, _matrix[minEdge.dst][i]));
                }
            }
        }

        if (dstSize != size - 1)
        {
            // 没有找到生成树
            std::cout << "没有找到生成树" << std::endl;
            return w();
        }
        return total;
    }
};

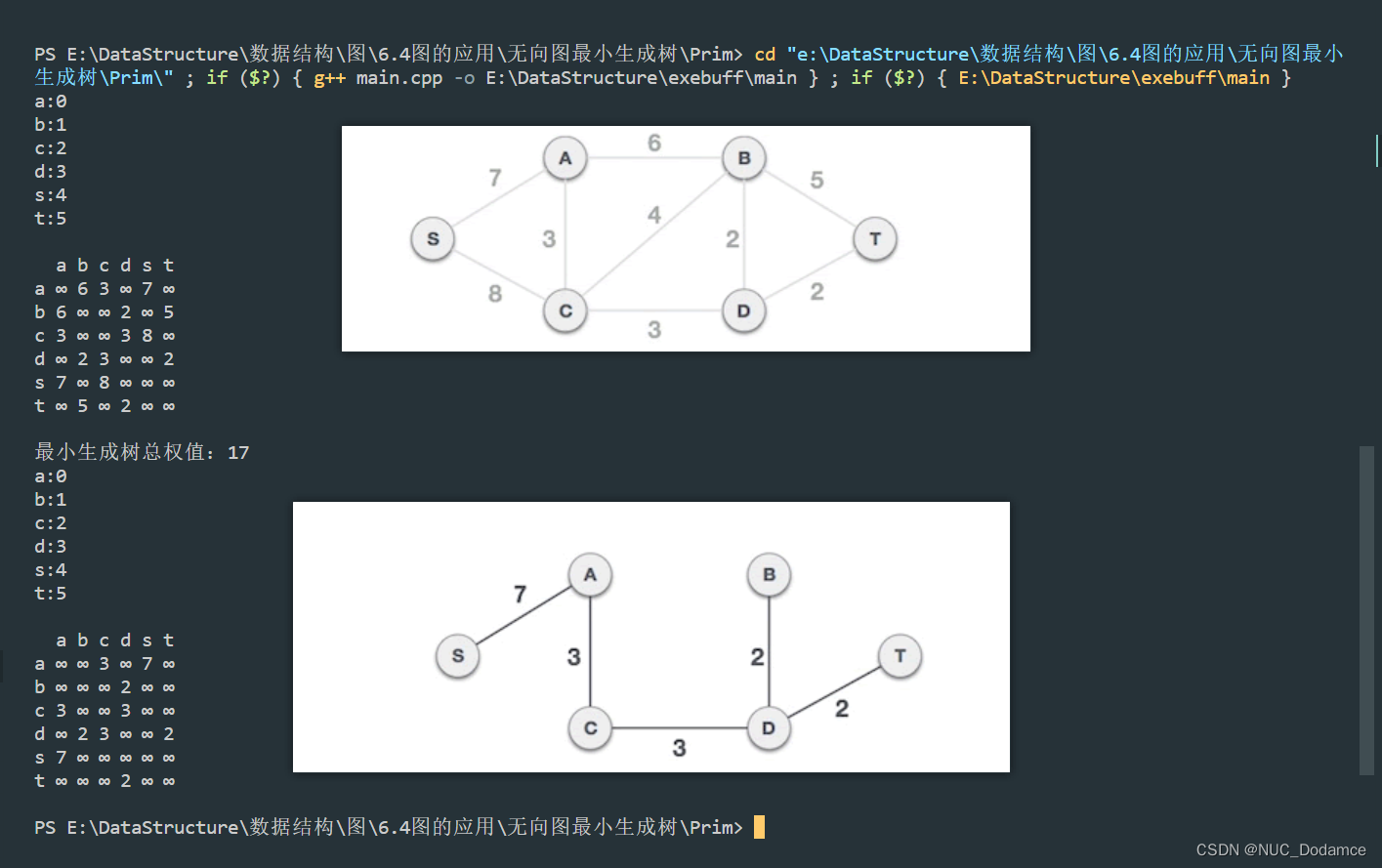
测试代码和结果

#include "matrix.h"

using namespace std;

int main(int argc, char const *argv[])
{
    vector<char> vet = {'a', 'b', 'c', 'd', 's', 't'};
    graph<char, int> Graph(vet);
    Graph.AddEdge('a', 'b', 6);
    Graph.AddEdge('b', 't', 5);
    Graph.AddEdge('t', 'd', 2);
    Graph.AddEdge('d', 'c', 3);
    Graph.AddEdge('c', 's', 8);
    Graph.AddEdge('s', 'a', 7);
    Graph.AddEdge('c', 'a', 3);
    Graph.AddEdge('c', 's', 8);
    Graph.AddEdge('b', 'd', 2);
    Graph.PrintGraph();

    graph<char, int> minGraph;
    cout << "最小生成树总权值：" << Graph.Prim(minGraph, 's') << endl;
    minGraph.PrintGraph();
    return 0;
}

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/124747.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

MySQL索引相关知识

MySQL索引相关知识

1、什么是索引&#xff1f; 索引是存储引擎用于提高数据库表的访问速度的一种数据结构。通过给字段​​添加索引​​​可以​​提高数据的读取速度​​​&#xff0c;提高项目的并发能力和抗压能力。​​索引优化​​​时mysql中的一种优化方式。索引的作用相当于​​图书的目录…
阅读更多...
一文搞懂Linux内核进程原理及系统调用机制

一文搞懂Linux内核进程原理及系统调用机制

进程四要素 有一段程序代其执行有进程专用的系统堆栈空间在内核有task_struct数据结构进程有独立的存储空间&#xff0c;拥有专有的用户空间 如果具备前三点缺少第四条&#xff0c;称为“线程”&#xff1b;如果完全没有用户空间&#xff0c;称为“内核线程”;如果共享用户空间…
阅读更多...
中国剩余定理

中国剩余定理

最近总是用到中国剩余定理&#xff0c;以前对于这个定理非常的模糊&#xff0c;有时间静下心来简单的学习一下中国剩余定理&#xff0c;文章没有深度&#xff0c;写下这篇博客以作记录。 中国剩余定理CRT前言一、描述二、中国剩余定理求解方法1.除以三余二2.除以五余三3.除以七…
阅读更多...
14. UserAgent 反爬是如何实现的，来看看这篇博客

14. UserAgent 反爬是如何实现的，来看看这篇博客

本篇博客实现 【爬虫训练场】 的第一个反爬案例&#xff0c;User-Agent 反爬。 文章目录什么是 User-Agent 反爬在 Python Flask 中实现 User-Agent 反爬什么是 User-Agent 反爬 User-Agent 反爬是一种防止网站被爬虫爬取的技术。 当爬虫向网站发送 HTTP 请求时&#xff0c;会…
阅读更多...
初识Kubernetes：（3）Kubernetes资源管理

初识Kubernetes：（3）Kubernetes资源管理

初识Kubernetes&#xff1a;&#xff08;3&#xff09;Kubernetes资源管理1 资源管理介绍2 YAML语法介绍2.1 YAML语法介绍2.2 YAML语法示例2.2.1 YAML常量2.2.2 对象2.2.3 数组3 资源管理方式3.1 资源管理方式3.2 命令式对象管理3.2.1 kubectl命令3.2.2 操作&#xff08;comman…
阅读更多...
操作系统期末考试必会题库2——进程管理

操作系统期末考试必会题库2——进程管理

1、某系统出现故障&#xff0c;通过相关指令查看&#xff0c;CPU占有率为0&#xff0c;内存有大量空余&#xff0c;但是用户在其程序中得不到任何相应&#xff0c;请从进程状态分析&#xff0c;当前用户所使用的进程可能是什么状态&#xff08;就绪&#xff0c;运行&#xff0c…
阅读更多...
BLE 蓝牙抓包分析

BLE 蓝牙抓包分析

1. 抓包工具 Ellisys & Ellisys Bluetooth Analyzer ​使用方法&#xff1a;https://blog.csdn.net/weixin_44260005/article/details/121216529​ 2. BLE数据样式 3. 数据分析 3.1 ble蓝牙协议栈 3.2 BLE连接过程 http://doc.iotxx.com/BLE%E6%8A%80%E6%9C%AF%E6%8F%AD%…
阅读更多...
如何用Alluxio加速云上深度学习训练？

如何用Alluxio加速云上深度学习训练？

欢迎来到【微直播间】&#xff0c;2min纵览大咖观点 随着企业数据量的不断增加&#xff0c;为了提高深度学习训练的准确性、加快速度并且降低成本&#xff0c;许多企业开始逐步在云上实施分布式训练的方案&#xff0c;本期内容将结合阿里、微软等实际应用案例&#xff0c;分享…
阅读更多...
容器安装mysql

容器安装mysql

1.自己配置仓库和挂载 仓库内容如下 挂载 2.安装工具包 yum install -y yum-utils 3.从阿里云添加docker仓库 yum-config-manager --add-repo https://mirrors.aliyun.com/docker-ce/linux/centos/docker-ce.repo 我们就能查看到 4.cd回主目录开始一系列安装 yum install d…
阅读更多...
软件测评师教程之软件测试基础＜一＞更新中...

软件测评师教程之软件测试基础＜一＞更新中...

目录一.软件测试分类(1)按照开发阶段划分(2)按照测试实施组织划分(3)按照测试技术划分二.软件测试过程模型(1)V模型(2)W模型(3)H模型(4)X模型(5)前置测试模型(6)测试模型的使用三.软件测试策略(1)测试信息流(2)分析设计阶段1.需求说明书评测2.概要设计说明书评测3.详细设计说明…
阅读更多...
手绘图说电子元器件-控制与保护器件

手绘图说电子元器件-控制与保护器件

控制与保护器件主要包括继电器、开关、接插件和保险器件等，是电子电路中经常使用的器件。 继电器 继电器是一种常用的控制器件，它可以用较小的电流来控制较大的电流，用低电压来控制高电压，用直流电来控制交流电等，并且可实现控制电路与被控电路之间的完全隔离。 继电…
阅读更多...
IPV6探测

IPV6探测

目录本机是否支持IPv6如何确认一个网站是否开启 IPv6在线工具&#xff1a;IP查询在线工具&#xff1a;IPv6连接测试在线工具&#xff1a;国家IPv6发展监测平台本地工具局域网设备探测pingMSFThc-Ipv6Ipv6-Toolkit端口探测MSFNmap【存在问题】参考领导提了个问题&#xff0c;怎么…
阅读更多...
Mybatis 解析mapper过程

Mybatis 解析mapper过程

Mapper配置的四种方式 配置方法一共有四种&#xff0c; 分别对应四种解析方式&#xff0c;从解析源码可以看出来 private void mapperElement(XNode parent) throws Exception { //添加接口映射器if (parent ! null) {for (XNode child : parent.getChildren()) { //获取所有…
阅读更多...
4.7W防削顶单声道D类音频功率放大器HT6872介绍

4.7W防削顶单声道D类音频功率放大器HT6872介绍

HT6872简介 HT6872是一款低EMI&#xff0c;防削顶失真&#xff0c;单声道免滤波D类音频功率放大器。在6.5V电源&#xff0c;10%THDN&#xff0c;4Ω负载条件下&#xff0c;输出4.71W功率&#xff0c;在各类音频终端应用中维持高效率并提供AB类放大器的性能。 HT6872的最大特点是…
阅读更多...
C++:设计一个保留字（或关键字）的统计程序,从源数据文件（C或C++语言程序）中，读取字符或字符串，与保留字文件中的保留字进行匹配比较，并统计计数。

C++:设计一个保留字（或关键字）的统计程序,从源数据文件（C或C++语言程序）中，读取字符或字符串，与保留字文件中的保留字进行匹配比较，并统计计数。

2.1题目&#xff1a; 设计一个保留字&#xff08;或关键字&#xff09;的统计程序 l建立保留字文件&#xff1b; l从源数据文件&#xff08;C或C语言程序&#xff09;中&#xff0c;读取字符或字符串&#xff0c;与保留字文件中的保留字进行匹配比较&#xff0c;并统计计数。…
阅读更多...
python数据分析（1）numpy基础

python数据分析（1）numpy基础

iamseancheney/python_for_data_analysis_2nd_chinese_version: 《利用Python进行数据分析第2版》 (github.com) NumPy的ndarray&#xff1a;一种多维数组对象 1.性质 NumPy最重要的一个特点就是其N维数组对象&#xff08;即ndarray&#xff09;&#xff0c;该对象是一个快速…
阅读更多...
73.qt quick-通用可拖拽表盘示例

73.qt quick-通用可拖拽表盘示例

截图如下所示: 效果如下所示: 源码已上传至专栏群(第一章底部获取)中,感兴趣的自行下载 demo使用介绍 控件自定义属性已经封装出来了,如下图所示: main.qml如下所示: import QtQuick 2.14 import QtQuick.Window 2.14 import QtQuick.Extras 1.4 import QtQuick.Layouts 1.1…
阅读更多...
微信小程序-会议OA项目03

微信小程序-会议OA项目03

目录 1.Flex布局简介 1.1 什么是flex布局 1.2 flex属性 2.轮播图--组件的使用 3.会议OA项目-首页 1.Flex布局简介 布局的传统解决方案&#xff0c;基于盒状模型&#xff0c;依赖 display属性 position属性 float属性 1.1 什么是flex布局 1) Flex是Flexible Box的缩写&…
阅读更多...
攻防世界-fileclude

攻防世界-fileclude

题目 访问题目场景 阅读php代码 <?php include("flag.php"); highlight_file(__FILE__); if(isset($_GET["file1"]) && isset($_GET["file2"])) {$file1 $_GET["file1"];$file2 $_GET["file2"];if(!empty($f…
阅读更多...
法国半导体制造企业RIBER部署MBE技术以支持量子计算

法国半导体制造企业RIBER部署MBE技术以支持量子计算

图片来源&#xff1a;网络 法国半导体制造企业RIBER在2022年进一步提升了其在量子处理器耗材市场的发展水平。 早在2021年6月&#xff0c;RIBER已开始部署系统&#xff0c;它在法国图卢兹与 法国国家科学研究中心系统分析与架构实验室&#xff08;LAAS-CNRS&#xff09;创办联合…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023