最近总是用到中国剩余定理，以前对于这个定理非常的模糊，有时间静下心来简单的学习一下中国剩余定理，文章没有深度，写下这篇博客以作记录。

---

前言

中国剩余定理又称孙子定理或中国余数定理，是数论中的一个关于一元线性同余方程组的定理，说明了一元线性同余方程组有解的准则以及求解方法。在古代称为孙子定理、鬼谷算、秦王暗点兵、物不知数等。

---

一、描述

在古代中，“物不知其数”中的表述如下：

有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？

大概的意思就是一个整数除以三余二，除以五余三，除以七余二，求这个整数。在《孙子算经》中首次提到了同余方程组问题，并且给出了该问题的解法，因此在中文数学文献中也会将中国剩余定理称为孙子定理。可见我国古代的人是非常的聪明的。

---

古代的数学家对上面的问题“物不知其数”问题做出了完整系统的解答，并编出来了口诀（太厉害了！）

三人同行七十希，五树梅花廿一支，七子团圆正半月，除百零五便得知

这句话的意思就是除以三的余数乘七十，除以五的余数乘二十一，除以七余数乘十五，得到的结果就是即为加上一百零五的整数倍。
对“物不知其数”问题进行解答即可得到

70×2＋21×3＋15× 2=233=2 ×105＋23.

即解为23

二、中国剩余定理求解方法

使用中国剩余定理对“物不知其数”该问题进行解答，列出来线性同余方程组如下：

我们来分开对方程组求解，大概的思路如下：

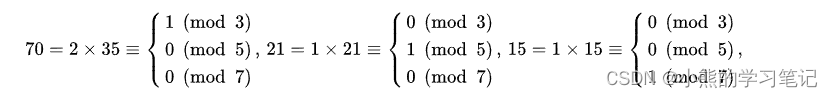
数a除以三等于一，除以五等于零，除以七等于零；数b除以三等于零，除以五等于一，除以七等于零；数c除以三等于零，除以五等于零，除以七等于一。
a乘除以三的余数，b乘除以五的余数，c乘除以七的余数。即上面求解“物不知其数”口诀的意思。

1.除以三余二

我们可以先找出一个整数a除以三等于一，除以五等于零，除以七等于零

5*7=35：35的倍数即可以保证除以五等于零，除以七等于零。
35（mod3）=2
35×2（mod3）=1

即该整数a为70
这也就是“三人同行七十希”

70（mod3）=1
70（mod5）=0
70（mod7）=0

则”除以三等于二，除以五等于零，除以七等于零“的整数a‘即为70×除于三的余数：即70×2=140

140（mod3）=2
140（mod5）=0
140（mod7）=0

---

2.除以五余三

我们可以先找出一个整数b除以五等于一，除以三等于零，除以七等于零

3*7=21：21的倍数即可以保证除以三等于零，除以七等于零。
21（mod5）=1

即该整数a为21
这也就是“五树梅花廿一支”

21（mod3）=0
21（mod5）=1
21（mod7）=0

则”除以五等于三，除以三等于零，除以七等于零“的整数b‘即为21×除于五的余数：即21×3=63

63（mod3）=0
63（mod5）=3
63（mod7）=0

3.除以七余二

我们可以先找出一个整数c除以七等于一，除以三等于零，除以五等于零

3*5=15：15的倍数即可以保证除以三等于零，除以七等于零。
15（mod7）=1

即该整数c为15
这也就是“七子团圆正半月“

15（mod3）=0
15（mod5）=0
15（mod7）=1

则”除以七等于二，除以三等于零，除以七等于零“的整数c‘即为15×除于五的余数：即15×2=30

30（mod3）=0
30（mod5）=0
30（mod7）=2

4.结论

最后的解为：a‘+b’+c’=140+63+30=233
3、5、7的最小公倍数为105

即该解为：233+n×105
n最小为-2：此时最小的正整数解为23

总结

用现代数学的语言来说明的话，中国剩余定理给出了以下的一元线性同余方程组：

假设整数m1,m2,m3…mn两两互素，则对于任意的整数x，满足以上方程组。则：

不得不感叹中国的古人是有大智慧的！
如有错误之处，感谢指正！